常用的图的存储结构主要有两种,一种是采用数组链表(邻接表)的方式,一种是采用邻接矩阵的方式。当然,图也可以采用十字链表或者边集数组的方式来进行表示,但由于不常用,为此,本博文不对其进行介绍。
邻接矩阵
邻接矩阵采用一个n*n的二维数组来进行表示(假设该二维数组为a),其中n表示的是图中节点的数目。当数组a[i][j]=1时,表示节点i有指向节点j的边。a[x][z]=0表示节点x没有指向节点z的边。因此,我们可以知道,对于无向图而言,领接矩阵为一个对称矩阵。其举例如下:
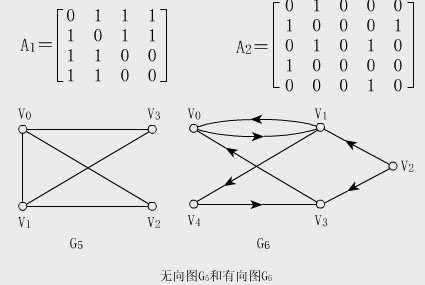
从中我们可以知道,对于一个邻接矩阵而言,其空间复杂度为O(n^2)。如果图的节点x和节点z之间的边上有权,我们可以将a[x][z]=x与z边上的权,若节点x和节点z不相连,可以将a[x][z]=无穷,采用这种方式,可以记录下图中的各边的情况。当图中边数较少的时候,将图存储为邻接矩阵的形式时,其邻接矩阵为一个稀疏矩阵,为此,我们又可以采用稀疏矩阵的压缩存储方式对其进行存储。此处不对稀疏矩阵的压缩存储方式进行介绍
邻接表
邻接表是图的另一种常见的存储结构,其采用数组+链表的方式对图结构进行存储。其具体为将图中的每一个顶点用一个链表来进行存储,链表中存储的为相邻顶点的编号。其示例图如下:
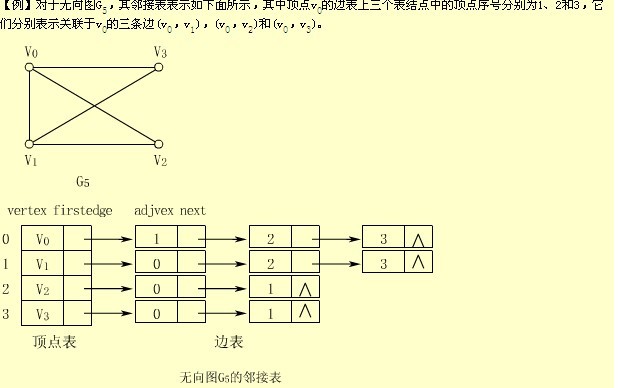
由此可知,采用该种方式进行存储的图结构,其空间复杂度为O(n+e),n为顶点数,e为图的边数