狄利克雷卷积 与 杜教筛

先放上板题
BZOJ3944
洛谷P4213

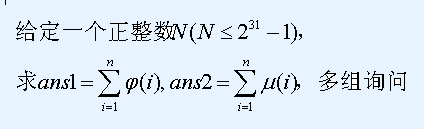
嗯，杜教筛解决的就是这样一个丧心病狂的前缀和
(O(N))都会T。。

积性函数##

如果一个数论函数(f(n))，满足若(m,n)互质，那么有(f(n * m) = f(n) * f(m))，那么称(f(n))为积性函数

特别的，如果对于任意(n,m)都满足(f(n * m) = f(n) * f(m))，那么称(f(n))为完全积性函数

狄利克雷卷积##

对于两个积性函数(f(n),g(n))，定义它们的狄利克雷卷积为：((f*g)(n) = sum_{d|n} f(d) * g(frac{n}{d}))
数论函数与狄利克雷卷积形成群，满足结合律，封闭性，单位元，逆元，同时还满足交换律

其中单位元为(epsilon)，(epsilon(n) = [n = 1])
还有一些比较常用的积性数论函数

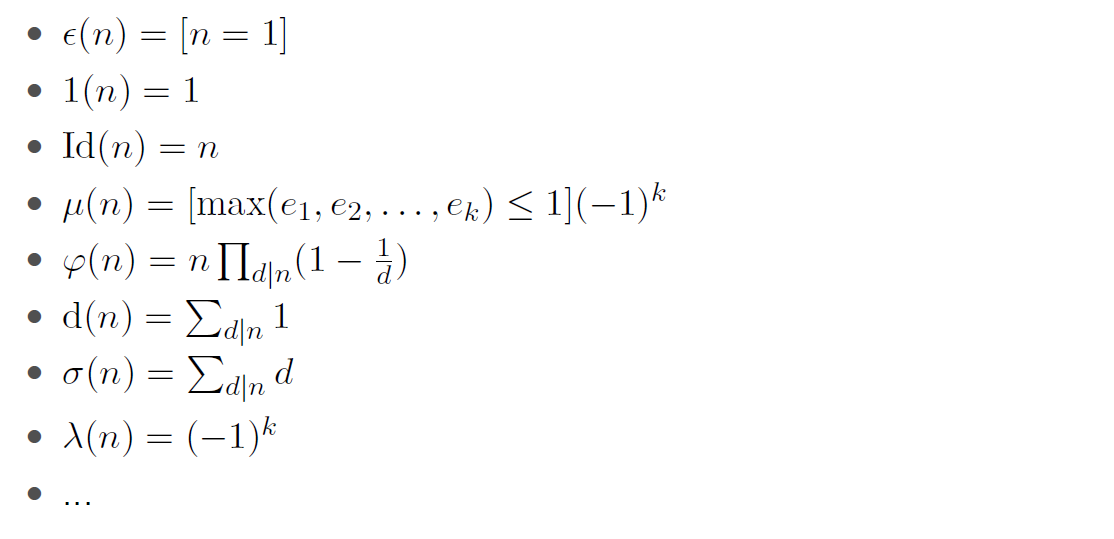
这里有比较常用的几种卷积关系：
(mu * 1=epsilon)【莫比乌斯反演】【(mu)与(1)互为逆元】
(phi * 1=Id) (qquad phi = Id * mu)
(d = 1 * 1) (qquad 1 = mu * d)
等等之类的，，

我们甚至可以简单地证明莫比乌斯反演了：

[F = f * 1 ]

[f = mu * F ]

杜教筛##

说了那么多，回归到杜教筛吧：
我们要求的是:

[S(n) = sum_{i=1}^{n} f(i) ]

我们找到另一个积性数论函数(g(n))
那么

[sum_{i=1}^{n}(f*g)(i) = sum_{i=1}^{n} sum_{d|i} g(d) * f(frac{i}{d}) ]

[qquad qquad = sum_{i=1}^{n} g(i) * sum_{j = 1}^{lfloor frac{n}{i} floor} f(j) ]

[qquad qquad = sum_{i=1}^{n} g(i) * S(lfloor frac{n}{i} floor) ]

我们就有：

[sum_{i=1}^{n}(f*g)(i) = sum_{i=1}^{n} g(i) * S(lfloor frac{n}{i} floor) ]

就可以有：

[g(1) * S(n) = sum_{i=1}^{n}(f*g)(i) - sum_{i=2}^{n} g(i) * S(lfloor frac{n}{i} floor) ]

如果我们能找到一个函数(g(n))
使得(sum_{i=1}^{n}(f*g)(i))可以被快速计算
并且其前缀和非常容易计算【因为要计算(sum_{i=2}^{n} g(i) * S(lfloor frac{n}{i} floor))】
那么我们就可以 分块 + 递归 求解(S(n))了

可以证明，我们预处理出积性函数(f(n))的前(O(n^{frac{2}{3}}))项，就可以在记忆化搜索在(O(n^{frac{2}{3}}))的复杂度计算出(S(n))
是不是很神奇?

回到例题
具体地，两个问都可以考虑令(g = 1)
具体自行思考

呼啦啦写完啦
贴代码【洛谷AC，BZOJ RE不停，求助QAQ，，或者哪天我再查查】
【思路还是没问题】

#include<iostream>
#include<cstdio>
#include<cmath>
#include<map>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<' '; puts("");
using namespace std;
const int maxn = 100005,maxm = 4000005,N = 3414680,INF = 1000000000;
map<LL,LL> _mu,_phi;
int isn[maxm];
LL p[maxm],pi;
LL mu[maxm],phi[maxm];
void init(){
	mu[1] = 1; phi[1] = 1;
	for (register LL i = 2; i < N; i++){
		if (!isn[i]) p[++pi] = i,mu[i] = -1,phi[i] = i - 1;
		for (register int j = 1; j <= pi && i * p[j] < N; j++){
			isn[i * p[j]] = true;
			if (i % p[j] == 0){
				mu[i * p[j]] = 0;
				phi[i * p[j]] = phi[i] * p[j];
				break;
			}
			mu[i * p[j]] = -mu[i];
			phi[i * p[j]] = phi[i] * (p[j] - 1);
		}
	}
	for (register int i = 1; i < N; i++){
		mu[i] += mu[i - 1];
		phi[i] += phi[i - 1];
	}
}
LL S1(LL n){
	if (n < N) return phi[n];
	map<LL,LL>::iterator it;
	if ((it = _phi.find(n)) != _phi.end())
		return it->second;
	LL ans = n * (n + 1) >> 1;
	for (int i = 2,nxt; i <= n; i = nxt + 1){
		nxt = n / (n / i);
		ans -= (nxt - i + 1) * S1(n / i);
	}
	return _phi[n] = ans;
}
LL S2(LL n){
	if (n < N) return mu[n];
	map<LL,LL>::iterator it;
	if ((it = _mu.find(n)) != _mu.end())
		return it->second;
	LL ans = 1;
	for (int i = 2,nxt; i <= n; i = nxt + 1){
		nxt = n / (n / i);
		ans -= (nxt - i + 1) * S2(n / i);
	}
	return _mu[n] = ans;
}
int main(){
	init();
	LL T,n;
	scanf("%lld",&T);
	while (T--){
		scanf("%lld",&n);
		printf("%lld %lld
",S1(n),S2(n));
	}
	return 0;
}