题目链接
题解
拉格朗日乘数法
拉格朗日乘数法用以求多元函数在约束下的极值
我们设多元函数(f(x_1,x_2,x_3,dots,x_n))
以及限制(g(x_1,x_2,x_3,dots,x_n) = E)
我们需要求(f)在限制(g)下的极值
如图
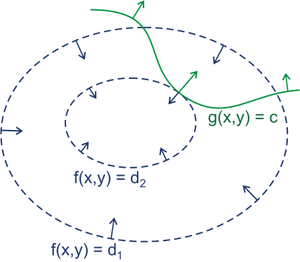
当(f)取到最值时,必然与(g)的等高线相切
所以我们只需找出这个切点
切点处两函数的梯度向量平行({
abla f~//~
abla g})
梯度向量的每一维就是该维下的偏导函数
[{
abla f=(frac{partial f}{partial x_1},frac{partial f}{partial x_2},frac{partial f}{partial x_3},dots,frac{partial f}{partial x_n})}
]
偏导可以理解为把别的变量看做常数,只对一个变量求导
所以只需令
[
abla f = lambda
abla g
]
可以得到(n)个方程,加上(g)本身就是一个方程
可以得到(n + 1)个方程,可解(lambda)以及(x_i)
本题
限制是
[sumlimits_{i = 1}^{n}s_ik_i(v_i - v'_i)^{2} = E
]
我们要最小化
[sumlimits_{i = 1}^{n}frac{s_i}{v_i}
]
利用拉格朗日乘数法,我们求出(n + 1)个方程
对于变量(x_i)的偏导,可得到方程
[2lambda k_iv_i^{2}(v_i - v'_i) = -1
]
首先(v_i ge v'_i),所以除(lambda)外左边是正的,所以(lambda)是负的,然后可以发现(v_i)关于(lambda)单调
而方程
[sumlimits_{i = 1}^{n}s_ik_i(v_i - v'_i)^{2} = E
]
左边也关于(v_i)单调,所以可以使用二分求解
当然求(v_i)也可以用牛顿迭代
还有就是精度要开够大。。
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<map>
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) make_pair<int,int>(a,b)
#define cls(s) memset(s,0,sizeof(s))
#define cp pair<int,int>
#define LL long long int
using namespace std;
const int maxn = 10005,maxm = 100005;
const double eps = 1e-13,INF = 1e12;
int n;
double E,v1[maxn],v[maxn],s[maxn],k[maxn];
inline double f(int i,double lam){
return 2 * lam * k[i] * v[i] * v[i] * (v[i] - v1[i]) + 1;
}
inline double cal(double lam){
REP(i,n){
double l = max(v1[i],0.0),r = INF;
while (r - l > eps){
v[i] = (l + r) / 2.0;
if (f(i,lam) >= 0) l = v[i];
else r = v[i];
}
v[i] = l;
}
double re = 0;
REP(i,n) re += s[i] * k[i] * (v[i] - v1[i]) * (v[i] - v1[i]);
return re;
}
int main(){
scanf("%d%lf",&n,&E);
REP(i,n) scanf("%lf%lf%lf",&s[i],&k[i],&v1[i]);
double l = -INF,r = 0,mid;
while (r - l > eps){
mid = (l + r) / 2.0;
if (cal(mid) >= E) r = mid;
else l = mid;
}
cal(l);
double ans = 0;
REP(i,n) ans += s[i] / v[i];
printf("%.10lf
",ans);
return 0;
}