zoukankan html css js c++ java

2016 Multi-University Training Contest 3

5/11

2016 Multi-University Training Contest 3
官方题解

2016年多校训练第三场老年选手历险记

暴力 A Sqrt Bo（CYD）

题意：
问进行多少次开根号向下取整能使给定的值为1，若为5次以上，则输出TAT；

思路：

有5次这个限制，得知值最大为10的11次方左右，存下后运算即可，注意初始值为0时运算的次数是大于5次的，输出TAT；

代码：

#include <bits/stdc++.h>
using namespace std;

char str[105];

int main()
{
    int i,j,k;
    while(scanf("%s",str)!=EOF)
    {
        double ans=0;
        int l=strlen(str);
        if(l>12 || (l==1 && str[0]=='0'))
        {
            printf("TAT
");
            continue;
        }
        for(i=0;i<l;i++)
        {
            ans=ans*10;
            ans+=str[i]-'0';
        }

        int cnt=0;
        while(ans-1.0>=1e-6)
        {
            ans=floor(sqrt(ans));
            cnt++;
        }
        if(cnt>5)
            printf("TAT
");
        else
            printf("%d
",cnt);
    }
    return 0;
}

线性期望 B Permutation Bo（BH）

题意：

　　有n个数字，范围1~n，对于一个排列，有 $f(h)=\sum_{i=1}^{n}c_i[h_i>h_{i-1} and h_i>h_{i+1}]$ ， $c_i$ 已知，后面意思是判断 $h_i$ 大于左右两边的数字，结果1或0，然后与 $c_i$ 相乘累加，求对于全排列，f(h)的期望值。

思路：

　　对于这种线性期望题，对于每一个 $h_i$ ，求它能贡献的概率*权值，权值已知，也就是要求 $h_i>h_{i-1}andh_i>h_{i+1}$ 在全排列出现的概率。易得概率为 $p_i=\frac{2\binom{n}{3}(n-3)!}{n!}=\frac{1}{3}(1<i<n)$ ， $p_i=\frac{\binom{n}{2}(n-2)!}{n!}=\frac{1}{2}(i=1ori=n)$ ，答案为 $ans=\sum_{i=2}^{n-1}c_i*pi$ 。

代码：

#include <bits/stdc++.h>

const int N = 1e3 + 5;
int c[N];

int main() {
    int n;
    while (scanf ("%d", &n) == 1) {
        int s1 = 0, s2 = 0;
        for (int i=1; i<=n; ++i) {
            scanf ("%d", c+i);
            if (i == 1 || i == n) s1 += c[i];
            else s2 += c[i];
        }
        double ans = 0;
        if (n == 1) {
            ans = c[1];
        } else {
            ans = (double) s1 / 2 + (double) s2 / 3;
        }
        printf ("%.6f
", ans);
    }
    return 0;
}

博弈/打表 Life Winner Bo（BH）

题意：

　　n*m的棋盘，在(1,1)的位置放一个国际象棋中的棋子（国王，车，骑士，皇后），国王相当于中国象棋的士的走法，车就是车，骑士相当于马（没有马脚），皇后有士的方向，车的距离。每次只能往右下走，B先走，问谁必胜。

思路：

　　反思：一开始我就想用从下往上递推状态图，写了四个函数分别是四个棋子的走法，对于车和皇后的后继状态比赛时先用了树状数组T了，后来用了数组求前缀后省了logn，但还是T了，一脸懵逼。后来才发现T<=1000，再加上我每次都 $O(n^2)$ 的跑，不T才怪。后来脑子清醒点再加上队友的指点，才想到还有预处理这条路，存下所有4*n*m的结果，然后 $O(1)$ 输出答案，结果还是以WA终场。赛后知道皇后是经典的威佐夫博弈，完全没听说过，博弈只会简单的递推。。。，

　　看完题解知道车原来就是经典的Nim，至于另外两个可以打表找规律也可以直接递推的。经检验，比赛的递推代码里只有皇后是有问题的，补题时打表找出马和国王的规律。代码里还留有递推的正确代码。

　　另外，只有马有平局的情况，出现这种可能的局面是B在没有必胜的可能情况下，平局比必败优，选择走平局的情况（往不能走的边界方向走）。

代码：

#include <bits/stdc++.h>

const int N = 1e3 + 5;
const int W = 1e3;
const double a = (sqrt (5.0) + 1) / 2;
int win[N][N];
int dp[4][N][N];  //1 2 3
int row[N][N], col[N][N];
int tp, n, m;

void debug() {
    for (int i=1; i<=20; ++i) {
        for (int j=1; j<=20; ++j) {
            printf ("%c ", dp[3][i][j]);
        }
        puts ("");
    }
}

char solve_rook() {
    return (n ^ m) ? 'B' : 'G';
}

char solve_queen() {
    if (n > m) std::swap (n, m);
    n--; m--;
    int k = m - n;
    if (n == (int) (a * k)) return 'G';
    else return 'B';
}

char solve_king() {
    if (n & 1 && m & 1) return 'G';
    else return 'B';
}

char solve_knight() {
    if (n == m) {
        if (n % 3 == 1 && n >= 4) return 'G';
        else return 'D';
    } else {
        if (n > m) std::swap (n, m);
        if (n + 1 == m && n % 3 == 2 && n >= 2) return 'B';
        else return 'D';
    }
}

void init() {
    n = m = W;
    //solve_king ();
    //solve_knight ();
    //solve_rook ();
    //solve_queen ();  //WA TAT
}

int main() {
    //init ();
    int T;
    scanf ("%d", &T);
    while (T--) {
        scanf ("%d%d%d", &tp, &n, &m);
        if (tp == 1) {
            printf ("%c
", solve_king ());
        } else if (tp == 2) {
            printf ("%c
", solve_rook ());
        } else if (tp == 3) {
            printf ("%c
", solve_knight ());
            //printf ("%c
", dp[tp][n][m]);
        } else {
            printf ("%c
", solve_queen ());
        }
    }
    return 0;
}


/*
void solve_rook() {
    memset (win, 0, sizeof (win));
    win[n][m] = 0;
    for (int i=n; i>=1; --i) {
        for (int j=m; j>=1; --j) {
            if (i == n && j == m) continue;
            win[i][j] = 0;
            if (j < m) {
                row[i][j] = row[i][j+1];
                if (row[i][j+1] != m - j) win[i][j] = 1;
            }
            if (i < n) {
                col[j][i] = col[j][i+1];
                if (col[j][i+1] != n - i) win[i][j] = 1;
            }

            if (win[i][j]) row[i][j]++, col[j][i]++;

            int nn = W - i + 1, mm = W - j + 1;
            dp[2][nn][mm] = win[i][j] ? 'B' : 'G';
        }
    }
}
*/
/*
void solve_king() {
    for (int i=n; i>=1; --i) {
        for (int j=m; j>=1; --j) {
            if (i == n && j == m) continue;
            if (j < m) {
                if (!win[i][j+1]) win[i][j] = 1;
                if (i < n && !win[i+1][j+1]) win[i][j] = 1;
            }
            if (i < n && !win[i+1][j]) win[i][j] = 1;
            int nn = W - i + 1, mm = W - j + 1;
            dp[1][nn][mm] = win[i][j] ? 'B' : 'G';
        }
    }
    debug ();
}*/
/*
void solve_knight() {
    memset (win, 0, sizeof (win));
    for (int i=1; i<=m; ++i) win[n][i] = -1;
    for (int i=1; i<=n; ++i) win[i][m] = -1;
    win[W-1][W-1] = -1;
    win[n][m] = 0;
    for (int i=n; i>=1; --i) {
        for (int j=m; j>=1; --j) {
            if (i == n && j == m) continue;
            if (win[i][j] == -1) continue;
            if (j < m && i < n-1 && !win[i+2][j+1]) win[i][j] = 1;
            if (j < m-1 && i < n && !win[i+1][j+2]) win[i][j] = 1;
            if (!win[i][j]) {
                if (j < m && i < n-1 && win[i+2][j+1] == -1) win[i][j] = -1;
                if (j < m-1 && i < n && win[i+1][j+2] == -1) win[i][j] = -1;
            }
            int nn = W - i + 1, mm = W - j + 1;
            dp[3][nn][mm] = win[i][j] == 1 ? 'B' : win[i][j] == 0 ? 'G' : 'D';
        }
    }
    debug ();
}
*/

物理 J Rower Bo（CYD）

题意：

给定x轴方向的水流速度、一艘船的初速度和在y轴上的起始位置，求船开到原点处的时间，船的方向总是朝向原点；

思路：

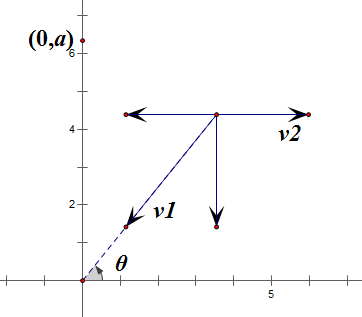
Alt text

$在x轴方向和朝向原点方向列出方程：$

$\frac{\partial r}{\partial t}=v1-v2*cos(\theta )$

$\frac{\partial x}{\partial t}=v2-v1*cos(\theta )$

$积分后得：$

$a-0=v1*T-v2*\int_{0}^{T}cos(\theta )dt$ ;

$0-0=v2*T-v1*\int_{0}^{T}cos(\theta )dt$

$T= \frac{v1*a}{v1^{2}-v2^{2}}$

$最后特判一下a=0和v1<=v2的情况。$

$代码：$

#include <bits/stdc++.h>
using namespace std;

int main()
{
    int a,v1,v2;
    while(scanf("%d %d %d",&a,&v1,&v2)!=EOF)
    {
        if(a==0)
        {
            printf("0.0000000000
");
            continue;
        }
        if(v1<=v2)
        {
            printf("Infinity
");
            continue;
        }
        double A=a,V1=v1,V2=v2;
        printf("%.10f
",V1*A/(V1*V1-V2*V2));
    }
    return 0;
}

鸽巢原理 K Teacher Bo（BH）

题意：

　　平面上n个点，要求判断是否存在两对点对（A，B）和（C，D)，使得点对的曼哈顿距离相同，点对可存在一个公共点。

思路：

　　看到题目上xi,yi<=M<=100000，

代码：

#include <bits/stdc++.h>

const int N = 1e5 + 5;
std::map<int, int> vis;

struct Point {
    int x, y;
}p[N];

int dis(Point &a, Point &b) {
    return abs (a.x - b.x) + abs (a.y - b.y);
}

int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        int n, m;
        scanf ("%d%d", &n, &m);
        bool flag = false;
        vis.clear ();
        for (int i=1; i<=n; ++i) {
            scanf ("%d%d", &p[i].x, &p[i].y);
            if (!flag) {
                for (int j=1; j<i; ++j) {
                    int d = dis (p[j], p[i]);
                    if (vis.count (d) == 0) {
                        vis[d] = 1;
                    } else {
                        flag = true;
                        break;
                    }
                }
            }
        }
        puts (flag ? "YES" : "NO");
    }
    return 0;
}

查看全文

相关阅读:
dedecms如何调用指定栏目下的相关文章
 dedecms二次开发标签总结
 如何在网页中显示数学公式与化学公式的方法
 CSS的选择器
 CSS属性之Overflow之作用
 FTP服务器架构简单方法
 dedecms性能选项与其它选项
 dedecms会员设置、互动设置
 dedecms图片设置属性
 dedecms核心设置

原文地址：https://www.cnblogs.com/NEVERSTOPAC/p/5708727.html