2016中国大学生程序设计竞赛

solved 5/11

2016中国大学生程序设计竞赛 - 网络选拔赛

大数取模 1001 A water problem（ZCJ&&BH）

题意：

　　判断n%10001=0？n的长度<=10000000。

思路：

　　这题不是我是AC的，但是看没人写就写点吧。大数取模，同余模定理，数字长度很长，用字符数组读入就好了。

代码：

#include <bits/stdc++.h>

const int N = 10000000 + 5;
char s[N];

int main() {
    int lcm = 10001;
    int cas = 0;
    while (scanf ("%s", s) == 1) {
        printf ("Case #%d: ", ++cas);
        int mod = 0;
        for (int i=0; s[i]; ++i) {
            mod = (mod * 10 + (s[i] - '0')) % lcm;
        }
        puts (!mod ? "YES" : "NO");
    }
    return 0;
}

数论+xor方程组消元 1002 Zhu and 772002（BH）

题意：

　　给n个数，选择一些数字乘积为平方数的选择方案数。（《训练指南》书上的例题）。

分析：

　　每一个数字分解质因数。比如4， 6， 10， 15，, , , , 令，表示选择第i个数字，那么，如果p是平方数，那么每个质因数上的指数为偶数，x1系数为2已经是偶数不考虑。可以转换为异或为0判断偶数，即奇数置为1，偶数置为0，然后n个数字m个质因数的增广矩阵消元看有几个自由变量(取0或1无所谓)，答案是2^r - 1(全部都不取方案不算)

代码：

#include <bits/stdc++.h>

const int N = 300 + 5;
const int P = 2000 + 5;
const int MOD = 1000000007;
const double EPS = 1e-8;
typedef long long ll;
typedef int Matrix[N][N];

bool is_prime[P];
int prime[P/2];

void prime_table(int n) {
    int &c = prime[0] = 0;
    memset (is_prime, true, sizeof (is_prime));
    is_prime[0] = is_prime[1] = false;
    for (int i=2; i<=n; ++i) {
        if (is_prime[i]) {
            prime[++c] = i;
            for (int j=i*2; j<=n; j+=i) {
                is_prime[j] = false;
            }
        }
    }
}

Matrix A;

void count_factors(int id, ll n, int &m) {
    for (int i=1; i<=prime[0]; ++i) {
        if (n % prime[i] == 0) {
            m = std::max (m, i);
            int p = prime[i];
            while (n % prime[i] == 0) {
                n /= prime[i];
                A[i-1][id] ^= 1;
            }
        }
    }
}

//xor_elimination
//m个方程，n个变量，求矩阵的秩
int rank(Matrix A, int m, int n) {
    int i = 0, j = 0, k, r, u;
    //处理第i个方程，第j个变量
    while (i < m && j < n) {
        r = i;
        for (k=i; k<m; ++k) {
            if (A[k][j]) {
                r = k;
                break;
            }
        }
        if (A[r][j]) {
            if (r != i) {
                for (k=0; k<=n; ++k) {
                    std::swap (A[r][k], A[i][k]);
                }
            }
            //消元后第i行的第一个非0列式第j列，第u>i的第j列均为0
            for (u=i+1; u<m; ++u) {
                if (A[u][j]) {
                    for (k=i; k<=n; ++k) {
                        A[u][k] ^= A[i][k];
                    }
                }
            }
            i++;
        }
        j++;
    }
    return i;
}

ll pow_mod(int x, int n) {
    ll ret = 1;
    for (; n; n>>=1) {
        if (n & 1) ret = ret * x % MOD;
        x = (ll) x * x % MOD;
    }
    return ret;
}

int main() {
    prime_table (2000);
    int T, cas = 0;
    std::cin >> T;
    while (T--) {
        int n;
        std::cin >> n;
        memset (A, 0, sizeof (A));
        int m = 0;
        for (int i=0; i<n; ++i) {
            ll x;
            std::cin >> x;
            count_factors (i, x, m);
        }
        int r = rank (A, m, n); //用到前m个素数
        printf ("Case #%d:
", ++cas);
        std::cout << ((pow_mod (2, n - r)) - 1 + MOD) % MOD << '
';  //n-r个自由变量，解集非空，所以-1
    }
    return 0;
}

树形DP 1003 Magic boy Bi Luo with his excited tree（BH）

题意：

　　有n个点的一棵树，点有价值，边有花费，问从一个节点出发能获得的最大价值（可以往返，价值只算一次，花费每次都算）。

思路：

　　一类典型的树形DP，之前做过几题（题目1，题目2），可惜做得少，不够系统。这类题都是两次DFS，第一次自底向上处理出节点往下的最优值，第二次自上向下，函数参数包含节点上面的最优值。dp[u][0]表示从u节点开始往它的子树下走，最终回到u的最大价值，dp[u][1]表示从u节点开始往它的子树下走，最终不回到u的最大价值，显然dp[u][1]>=dp[u][0]。如下图所示，红线表示往下，蓝线表示往上，dp[u][1]有一条最右边的红线

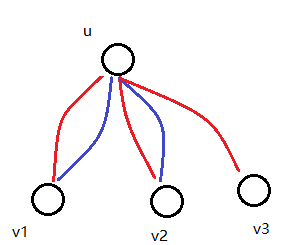
至于第二次DFS，根据往哪个儿子的子树走下去，更新最优的up1和up2即可。

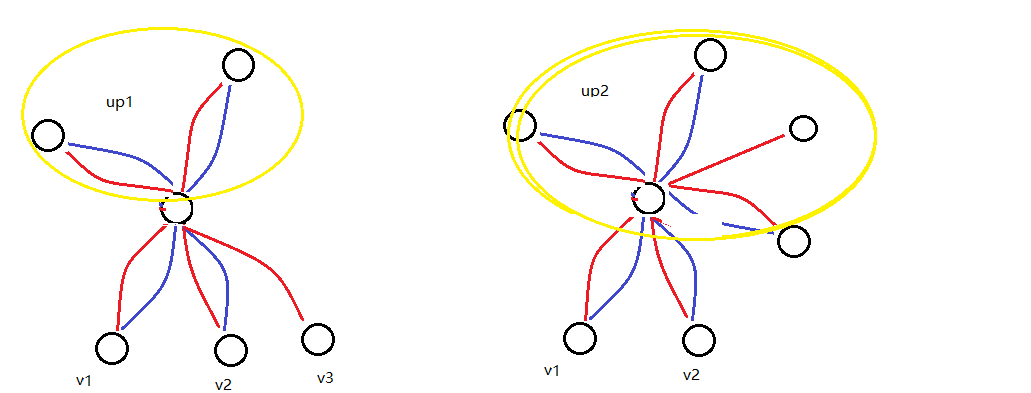
代码：

#include <bits/stdc++.h>

const int N = 1e5 + 5;
struct Edge {
    int v, c;
};
std::vector<Edge> edges[N];
int val[N];
int son[N];
int ans[N];
int n;

int dp[N][2];

//得到dp[u][0/1]
void DFS(int u, int fa) {
    dp[u][0] = dp[u][1] = val[u];
    son[u] = -1;  //dp[u][1] 从哪个儿子出发不回来
    for (Edge &e: edges[u]) {
        if (e.v == fa) continue;
        DFS (e.v, u);
        int tmp1 = std::max (0, dp[e.v][0] - e.c * 2);
        int tmp2 = dp[u][0] + std::max (0, dp[e.v][1] - e.c);
        dp[u][0] += tmp1;
        dp[u][1] += tmp1;
        if (dp[u][1] < tmp2) {
            dp[u][1] = tmp2;
            son[u] = e.v;
        }
    }
}

//up1：从u出发，不进入u的子树，最终返回u的最优值，up2：最终不返回u的最优值
void DFS(int u, int fa, int up1, int up2) {
    ans[u] = std::max (dp[u][0]+up2, dp[u][1]+up1);
    int s = son[u];
    int sum1 = up1 + dp[u][0];
    int sum2 = up1 + dp[u][1];
    if (sum2 <= up2 + dp[u][0]) {
        sum2 = up2 + dp[u][0];
        s = -1;
    }
    for (int i=0; i<edges[u].size (); ++i) {
        Edge &e = edges[u][i];
        if (e.v == fa)
            continue;
　　　　//类似第一个DFS的做法，也就是dp[u][0/1]的次优值
        if (e.v == s) {
            int new_up1 = up1 + val[u];
            int new_up2 = up2 + val[u];
            for (int j=0; j<edges[u].size (); ++j) {
                Edge &e2 = edges[u][j];
                if (e2.v == fa || e2.v == e.v)
                    continue;
                int tmp1 = std::max (0, dp[e2.v][0] - e2.c*2);
                int tmp2 = new_up1 + std::max (0, dp[e2.v][1] - e2.c);
                new_up1 += tmp1;
                new_up2 += tmp1;
                new_up2 = std::max (new_up2, tmp2);
            }
            new_up1 = std::max (0, new_up1 - e.c*2);
            new_up2 = std::max (0, new_up2 - e.c);
            DFS (e.v, u, new_up1, new_up2);
        } else {
　　　　　　//sub：去掉sum1里面e.v的贡献
            int sub = std::max (0, dp[e.v][0] - e.c*2);
            int new_up1 = std::max (0, sum1 - sub - e.c*2);
            int new_up2 = std::max (0, sum2 - sub - e.c);
            DFS (e.v, u, new_up1, new_up2);
        }
    }
}

void solve(int cas) {
    DFS (1, 0);
    DFS (1, 0, 0, 0);

    printf ("Case #%d:
", cas);
    for (int i=1; i<=n; ++i) {
        printf ("%d
", ans[i]);
    }
}

int main() {
    int T;
    scanf ("%d", &T);
    for (int cas=1; cas<=T; ++cas) {
        scanf ("%d", &n);
        for (int i=1; i<=n; ++i)
            scanf ("%d", val+i);
        for (int i=1; i<=n; ++i)
            edges[i].clear ();
        for (int i=1; i<n; ++i) {
            int u, v, c;
            scanf ("%d%d%d", &u, &v, &c);
            edges[u].push_back ((Edge) {v, c});
            edges[v].push_back ((Edge) {u, c});
        }
        solve (cas);
    }
    return 0;
}

贪心 1004 Danganronpa（BH）　　

题意：

　　每个小朋友两件礼物，相邻的小朋友普通礼物不能相同，神秘礼物没限制，问最多能分给几个小朋友。

思路：

　　考虑普通礼物，相邻的不同，取数量最多的两种礼物AB，分发为ABABAB。。。将剩余的放回优先队列里面（sort一下）直到已分发的数量小于剩余的数量。数据水得sum/2也能过。。。

代码：

#include <bits/stdc++.h>

int n;
int a[15];

bool cmp(int x, int y) {
    return x > y;
}

int solve() {
    if (n == 1) {
        return a[1] > 1;
    }
    int ret = 0, res = 0;
    for (int i=1; i<=n; ++i)
        res += a[i];
    int mx = res / 2;
    while (res > ret) {
        std::sort (a+1, a+1+n, cmp);
        int mn = std::min (a[1], a[2]);
        if ((res - mn * 2) <= ret + mn * 2) {
            int x = (res + ret) / 2;
            ret += x;
            break;
        } else {
            res -= mn * 2;
            a[1] -= mn;
            a[2] -= mn;
            ret += mn * 2;
        }
        if (res == ret)
            break;
    }
    return std::min (ret, mx);
}

int main() {
    int T;
    scanf ("%d", &T);
    for (int cas=1; cas<=T; ++cas) {
        scanf ("%d", &n);
        for (int i=1; i<=n; ++i) {
            scanf ("%d", a+i);
        }
        printf ("Case #%d: %d
", cas, solve ());
    }
    return 0;
}

水题 1011 Lweb and String（ZCJ）