神经网络基础知识以及Rosenblatt感知器

目录

• 0. 从零开始
• 1. 激活函数
  • 1.1 sigmoid函数
    • 1.1.1 logistic函数
    • 1.1.2 双曲正切函数
    • 1.1.3 阈值函数
• 2. Rosenblatt感知器
  • 2.1 Rosenblatt感知器伪代码
  • 2.2 Rosenblatt感知器的可视化向量理解
  • 2.3 Matlab代码：
• 参考

0. 从零开始

 最近开始学习神经网络与机器学习，学校的暑期课程学习曲线比较陡，老师默认我们已经具备了很多基础知识了，所以学起来很费力。所以就把自己的一些理解总结起来，放在这里，供参考。

1. 激活函数

1.1 sigmoid函数

• sigmoid函数是可微分的

1.1.1 logistic函数

• 修改参数a可以改变曲线的倾斜程度
  -化成伪温度T的形式后，T即用来控制噪声水平的不确定性，当T趋于0时，该函数趋近阈值函数

[phi( u) = frac{1}{1 + exp{(-a u)}} = frac{1}{1 + exp( frac{- u}{T} )} ]

1.1.2 双曲正切函数

• 允许激活函数取负值
• 值域为((-1 , 1 ))

[phi( u) = tanh( u) = frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} ]

1.1.3 阈值函数

• 比如最简单的符号函数就是一种阈值激活函数
• 不可微分

[ sgn( u)=left{ egin{aligned} +1, u geq 0 \ -1, u < 0 end{aligned} ight. ]

2. Rosenblatt感知器

 Rosenblatt感知器能够对于线性可分的数据很好地分类，而其中机理与SVM、似然函数之类的方法不同。它包含了一个隐含的损失函数，同时也是可用用夹逼定理证明严格收敛的[2]。

2.1 Rosenblatt感知器伪代码

输入：带标签的数据，其中输入数据为m维，且共有N组数据，标签(l)为阈值函数：

[X = { x^i , l^i } | i = 1,2,...N }, x^i = (x_1^i, x_2^i,...,x_m^i), l^i in {+1, -1 } ]

伪代码实现过程（参考1，不过做了一定的修改）：
for i = 1,2,...,N:
  (widehat{x}^i = (1 , x^i) = (1, x_1^i, x_2^i,..., x_m^i)) // 对于内部偏置量的升维
  (widehat{x}^{'i} = widehat{x}^{i}l^{i}) // 利用标签label实现对于输入数据的重新处理，方便后面直接采用
float w =< (m + 1) random float number >; // 随机产生m+1维需要估计的参数
float (eta) = ; // 学习率参数，通常取1，其实无所谓的，只是影响收敛速度
boollean errorDetect = true ;
while(errorDetected)
{
  errorDetected = false;
  for i = 1,2,...,N:
  if( $w^{{T}widehat{x}}{'i} < 0 $ ):
   errorDetected = true ;
   (w = w + {eta}widehat{x}^{'i})
}
最终输出：(w)

2.2 Rosenblatt感知器的可视化向量理解

 考虑最简单的一维数据的情况：

• 一维数据分布在坐标轴上：
  

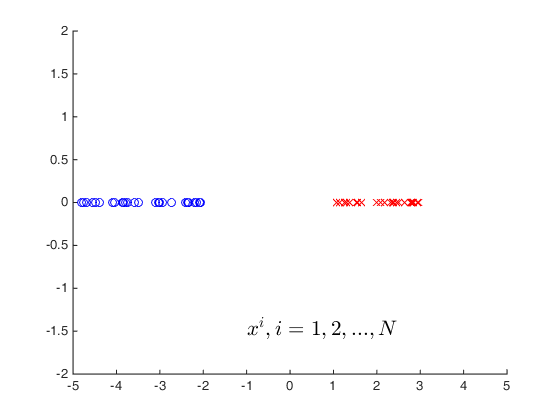
• 数据升维处理：
   此时，为了数据线性可分，权重向量(w)应当同图中的红色的点与原点构成的向量在90°以内，同蓝色的点与原点构成的向量在90°以外；反之亦可，即保证，权重向量与可分数据向量的内积分别为正负。
  

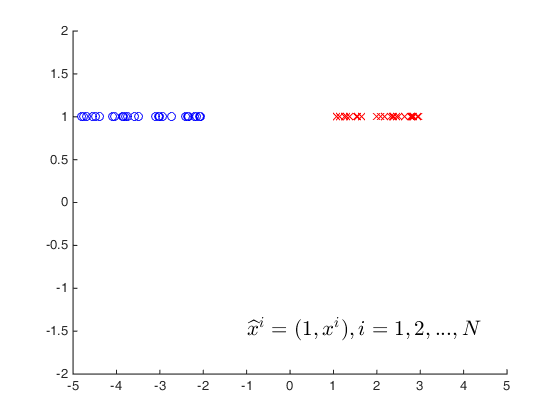
• 与标签量相乘处理：
   这就等价于将蓝色的向量绕原点旋转180°，此时只需要权重向量与两类向量的角度都在90°以内就满足线性可分的要求了。
  

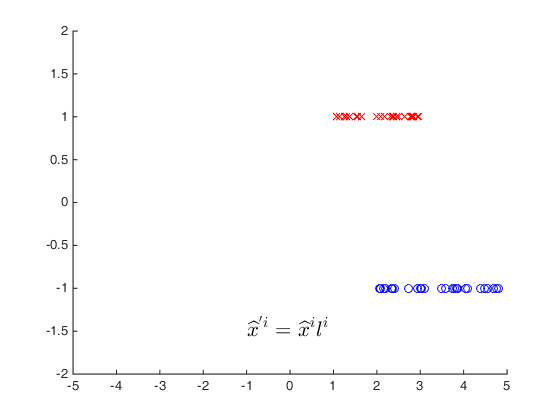
• 这里说的比较简单，只考虑了一维数据的情形，不过便于对于Rosenblatt工作原理的理解。

2.3 Matlab代码：

clear;
clc ;
 
x1 = 1 + 2 * rand(25 , 1) ;
x2 = -2 - 3 * rand(30 , 1 ) ;
 
x11 = [ones(size(x1)) x1 ];
x22 = [- ones(size(x2)) -x2 ];
x = [x11 ; x22 ];
w = [0 ,0 ]; % 任意取的
 
errorDetected = 1 ; 
counter = 0 ;
while errorDetected == 1
        errorDetected = 0 ;
        for i = 1:size(x , 1)
            counter = counter + 1 ;
            if(w * x(i, :)' <= 0)
                errorDetected = 1 ;
                w = w + x(i, :) ;
            end
        end
end
        
w = w/norm(w); % 向量归一化，便于显示
temp = [w ;zeros(1 , 2 )];
 
figure(1)
scatter(x1 ,zeros(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 权重向量为黑线
scatter(x2 ,zeros(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
 
text('Interpreter','latex','String','$$x^i, i = 1,2,...,N$$','Position',[-1 , -1.5],'FontSize',16);
hold off ;
 
figure(2)
scatter(x1 ,ones(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 权重向量为黑线
scatter(x2 ,ones(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
text('Interpreter','latex','String','$$widehat{x}^i =( 1, x^i), i = 1,2,...,N$$','Position',[-1 , -1.5],'FontSize',16);
hold off ;
 
figure(3)
scatter(x1 ,ones(size(x1)) , 'xr');
hold on ;
plot(temp(: , 2) , temp(: , 1) , 'k' ); % 权重向量为黑线
scatter(-x2 ,-ones(size(x2)) , 'ob');
set(gca , 'XLim' , [-5 5]);
set(gca , 'YLim' , [-2 2]);
text('Interpreter','latex','String','$$widehat{x}^{''i} = widehat{x}^{i}l^{i} $$','Position',[-1 , -1.5],'FontSize',16);
hold off ;

参考

1. Rosenblatt感知器详解
2. 神经网络与机器学习
3. C++代码实现