zoukankan html css js c++ java

红黑树插入 C语言实现

推荐一个红黑树可视化网站: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html

红黑树插入，按照排序二叉树规则插入即可，只不过插入后需要根据周边的节点来判断是否满足红黑树平衡，若不满足，需要进行染色或者旋转修复。

博客后面提供插入完整代码

1. 什么是红黑树

红黑树是一种自平衡二叉查找树，巴拉巴拉--- ，请注意前提，是一颗二叉查找树。

关于二叉查找树: https://baike.baidu.com/item/二叉排序树/10905079?fromtitle=二叉查找树&fromid=7077965&fr=aladdin

2. 红黑树概念

每个节点要么是红色，要么是黑色
根节点和叶节点是黑色的(红黑树的叶节点是NULL LEAF,默认NULL节点为黑色)
如果一个节点是红色，那么它的孩子是黑色的(不允许连续2个红节点，但是允许2个连续的黑节点)
任意节点到叶节点的树链中包含相同数量的黑节点

红黑树图示

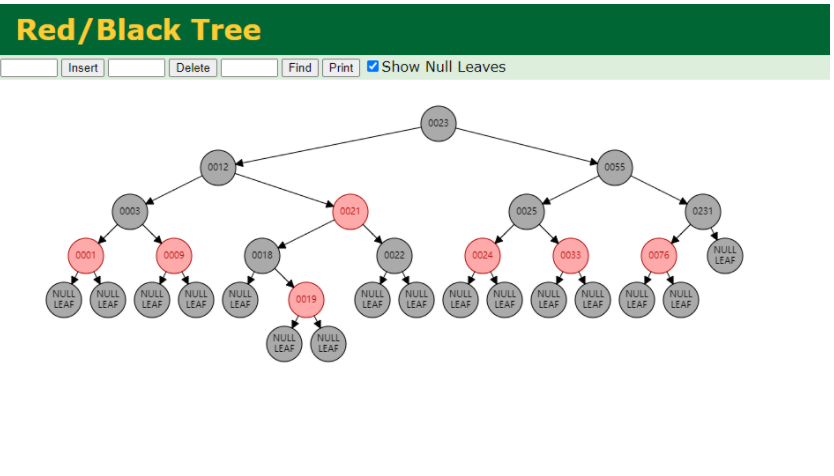
3. 红黑树插入后判断是否平衡以及何种操作

1. 判断是否平衡

若插入节点父节点为黑节点，则为平衡，无需修复。
若插入节点父节点为红色，叔叔节点为红色，则需要进行染色修复。
若插入节点父节点为红色，叔叔节点为黑色，则需要进行旋转。

2. 图示

ps: 黄色节点为新插入节点，一般默认新插入节点颜色为红色！

1. 被插入节点父节点为黑色，无需进行修复

2. 被插入节点父节点为红色，叔叔节点为红色，需要进行染色修复

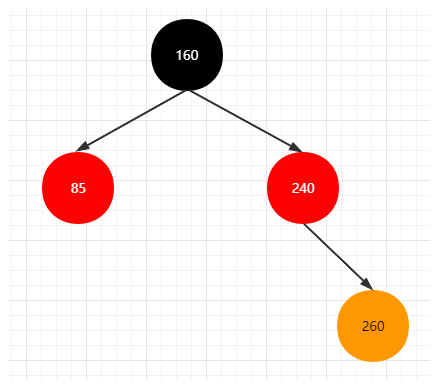
3. 被插入节点父节点为红色，叔叔节点为黑色(红黑树叶子节点都为黑色)，需要进行旋转操作

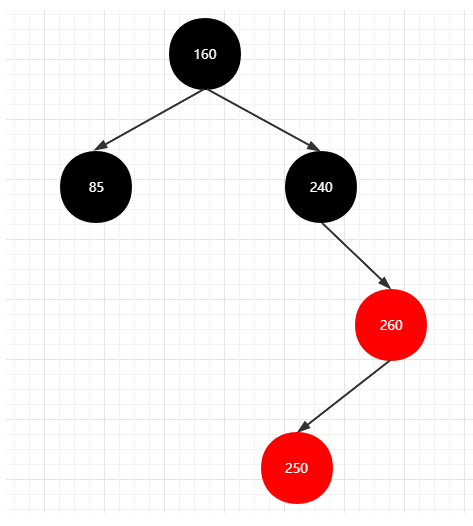
3. 测试代码实现

先看结论,再看核心和具体函数代码

3.1 插入是否需要修复结论

图示第一种情况

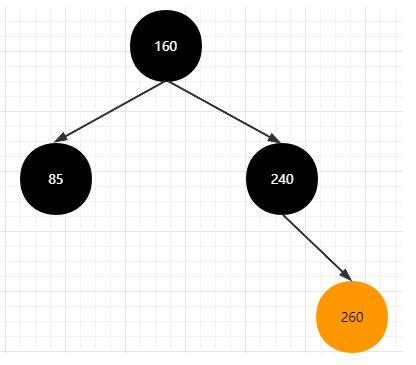
代码

int main() {
        TreeNode *root_160 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_85 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_240 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_260 = (TreeNode *)malloc(sizeof(TreeNode));

        root_160->data = 160; root_160->color = BLACK;
        node_85->data = 85; node_85->color = BLACK;
        node_240->data = 240; node_240->color = BLACK;
        node_260->data = 260; node_260->color = RED;

        root_160->left = node_85;
        root_160->right = node_240;
        node_240->right = node_260;

        InsertFixup1(&root_160,node_260);
        return 0;
}

执行结果

# gcc RedBlackTreeInsert.c -w -g
# ./a.out 
插入数据:260
无需进行修复
#

图示第二种情况

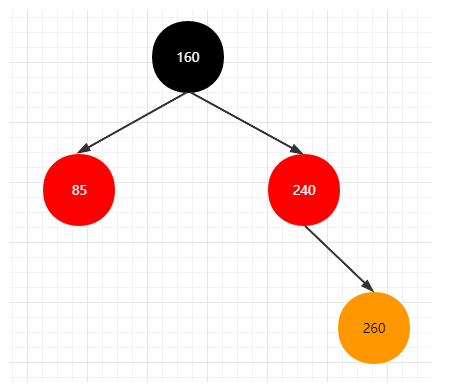
代码

int main() {
        TreeNode *root_160 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_85 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_240 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_260 = (TreeNode *)malloc(sizeof(TreeNode));

        root_160->data = 160; root_160->color = BLACK;
        node_85->data = 85; node_85->color = RED;
        node_240->data = 240; node_240->color = RED;
        node_260->data = 260; node_260->color = RED;

        root_160->left = node_85;
        root_160->right = node_240;
        node_240->right = node_260;

        InsertFixup1(&root_160,node_260);
        return 0;
}

执行结果

# gcc RedBlackTreeInsert.c -w -g
# ./a.out 
插入数据:260
需要进行染色修复
#

图示第三种情况

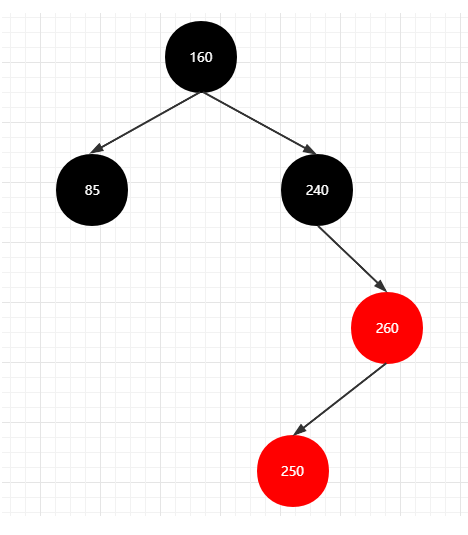
代码

int main() {
        TreeNode *root_160 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_85 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_240 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_260 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_250 = (TreeNode *)malloc(sizeof(TreeNode));

        root_160->data = 160; root_160->color = BLACK;
        node_85->data = 85; node_85->color = BLACK;
        node_240->data = 240; node_240->color = BLACK;
        node_260->data = 260; node_260->color = RED;
        node_250->data = 250; node_250->color = RED;

        root_160->left = node_85;
        root_160->right = node_240;
        node_240->right = node_260;
        node_260->left = node_250;

        InsertFixup1(&root_160,node_250);
        return 0;
}

执行结果

# ./a.out 
插入数据:250
需要进行旋转修复
#

3.2 核心代码

// 检测红黑树插入 是否需要修复
if ((parent->color == RED) && (uncleColor == RED)) {
    // 父亲节点为红色，叔叔节点为红色，需要进行染色修复
    printf("需要进行染色修复
");

} else if((parent->color == RED) && uncleColor == BLACK) {
    // 父节点为红色，叔叔节点为黑色，则需要进行旋转
    printf("需要进行旋转修复
");

} else {
    // 无需进行修复
    printf("无需进行修复
");

}

3.3 具体函数实现

宏定义/结构体

# include <stdio.h>
# include <stdlib.h>
# include <stdbool.h>

# define RED 1
# define BLACK 0

typedef struct {
        int data; // 数据节点
        struct TreeNode *left; // 左子树
        struct TreeNode *right; // 右字树
        int color;  // 二叉树颜色，1: 红色 0:黑色

} TreeNode , *PTreeNode;

具体函数

PTreeNode InsertFixup1(PTreeNode *root,PTreeNode newNode) {

        printf("插入数据:%d
",newNode->data);

        TreeNode *parent = NULL; // 父亲节点
        TreeNode *grandParent = NULL; // 爷爷节点 
        TreeNode *greatGrandParent = NULL; // 祖爷爷节点
        TreeNode *uncle = NULL; // 叔叔节点
        int uncleColor = 0; // 叔叔节点颜色，默认为黑色

        // 寻找节点 父亲/爷爷祖爷爷节点
        TreeNode *tmp = (*root);
        while (tmp != NULL) {
                if (newNode->data == tmp->data) {
                        break;
                }
                greatGrandParent = grandParent;
                grandParent = parent;
                parent = tmp;

                (newNode->data > tmp->data) ? (tmp = tmp->right) : (tmp = tmp->left);
        }

        // 当前节点是根节点，染成黑色
        if (newNode == (*root)) {
                printf("根节点，需要进行染色操作
");
        }
    
    	// 只有2层就退出去
        if (grandParent == NULL) return;
    
        // 获取叔叔节点
        (parent == grandParent->left) ? (uncle = grandParent->right) : (uncle = grandParent->left);

        // 获取叔叔节点颜色
        if (uncle != NULL) uncleColor = uncle->color;

    	// 检测红黑树插入 是否需要修复
        if ((parent->color == RED) && (uncleColor == RED)) {
                // 父亲节点为红色，叔叔节点为红色，需要进行染色修复
                printf("需要进行染色修复
");

        } else if((parent->color == RED) && uncleColor == BLACK) {
                // 父节点为红色，叔叔节点为黑色，则需要进行旋转
                printf("需要进行旋转修复
");

        } else {
                // 无需进行修复
                printf("无需进行修复
");
            
        }
}

4. 红黑树插入染色修复

染色修复

将父亲节点 和 叔叔节点 染成黑色。

将爷爷节点染成红色。

将爷爷节点赋值给当前节点 ，再次判断是否需要染色处理。

4.1 图示

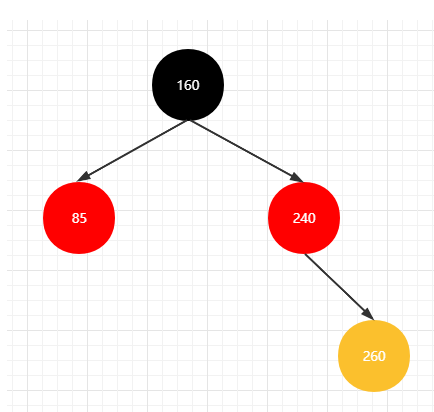
如上图所示，新插入节点为 260(当前节点) , 父亲节点为 240, 爷爷节点为 160, 叔叔节点为 85

4.2 染色处理

将父亲节点和叔叔节点染成黑色，爷爷节点染成红色，然后将当前节点挪至爷爷几点，再次判断是否需要染色处理。

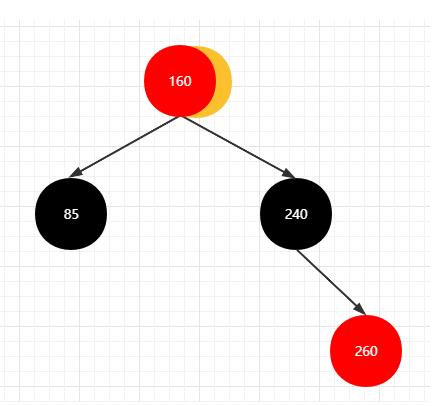
如上图所示，将父亲节点(240) 和叔叔节点 (85) 染成黑色后, 将爷爷节点(160)染成红色后，将当前节点挪至爷爷节点(160为红色节点，且当前节点指向160)，继续获取节点。

4.3 代码实现

核心代码

// 染色操作
if ((parent->color == RED) && (uncleColor == RED)) {
    parent->color = BLACK;
    uncle->color = BLACK;
    grandParent->color = RED;

    newNode = grandParent;
    continue;
}

染色完整代码

宏定义/结构体

# include <stdio.h>
# include <stdlib.h>
# include <stdbool.h>

# define RED 1
# define BLACK 0

typedef struct {
        int data; // 数据节点
        struct TreeNode *left; // 左子树
        struct TreeNode *right; // 右字树
        int color;  // 二叉树颜色，1: 红色 0:黑色

} TreeNode , *PTreeNode;

插入函数

PTreeNode InsertFixup1(PTreeNode *root,PTreeNode newNode) {

        printf("插入数据:%d
",newNode->data);

        TreeNode *parent = NULL; // 父亲节点
        TreeNode *grandParent = NULL; // 爷爷节点 
        TreeNode *greatGrandParent = NULL; // 祖爷爷节点
        TreeNode *uncle = NULL; // 叔叔节点
        int uncleColor = BLACK; // 叔叔节点颜色，默认为黑色

        while (true) {

                parent = grandParent = greatGrandParent = uncle = NULL;
                uncleColor = BLACK;

                // 寻找节点 父亲/爷爷祖爷爷节点
                TreeNode *tmp = (*root);
                while (tmp != NULL) {
                        if (newNode->data == tmp->data) {
                                break;
                        }
                        greatGrandParent = grandParent;
                        grandParent = parent;
                        parent = tmp;

                        (newNode->data > tmp->data) ? (tmp = tmp->right) : (tmp = tmp->left);
                }

                // 当前节点是根节点，染成黑色
                if (newNode == (*root)) {
                        printf("根节点，需要进行染色操作
");
                }

                if (grandParent == NULL) return;

                // 获取叔叔节点
                (parent == grandParent->left) ? (uncle = grandParent->right) : (uncle = grandParent->left);

                // 获取叔叔节点颜色
                if (uncle != NULL) uncleColor = uncle->color;



                if ((parent->color == RED) && (uncleColor == RED)) {
                        // 父亲节点为红色，叔叔节点为红色，需要进行染色修复
                        printf("需要进行染色修复
");

                        parent->color = BLACK;
                        uncle->color = BLACK;
                        grandParent->color = RED;

                        newNode = grandParent;
                        continue;

                } else if((parent->color == RED) && uncleColor == BLACK) {
                        // 父节点为红色，叔叔节点为黑色，则需要进行旋转
                        printf("需要进行旋转修复
");
                        break;


                } else {
                        // 无需进行修复
                        printf("无需进行修复
");
                        break;

                }
        }

}

主函数/遍历函数

// 前序遍历
void Print1(TreeNode *root) {
        if (NULL == root) return;
        printf("[颜色:%s  数据:%d]	",(root->color == RED) ? ("红"):("黑") ,root->data);
        Print1(root->left);
        Print1(root->right);
}

int main() {
        TreeNode *root_160 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_85 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_240 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_260 = (TreeNode *)malloc(sizeof(TreeNode));
        TreeNode *node_250 = (TreeNode *)malloc(sizeof(TreeNode));

        root_160->data = 160; root_160->color = BLACK;
        node_85->data = 85; node_85->color = 1;
        node_240->data = 240; node_240->color = 1;
        node_260->data = 260; node_260->color = RED;

        root_160->left = node_85;
        root_160->right = node_240;
        node_240->right = node_260;

        InsertFixup1(&root_160,node_260);
        Print1(root_160);
        printf("
");
        return 0;
}

执行结果

# ./a.out 
插入数据:260
需要进行染色修复
根节点，需要进行染色操作
[颜色:红  数据:160]     [颜色:黑  数据:85]      [颜色:黑  数据:240]     [颜色:红  数据:260]
#

5. 红黑树插入旋转修复

旋转修复

父亲节点为红色，叔叔节点为黑色，则需要进行旋转修复

而旋转修复又分为四种情况：左左/左右/右左/右右

5.1 图示

黄色节点为新插入节点，重点关注蓝色框框的树

左左情况

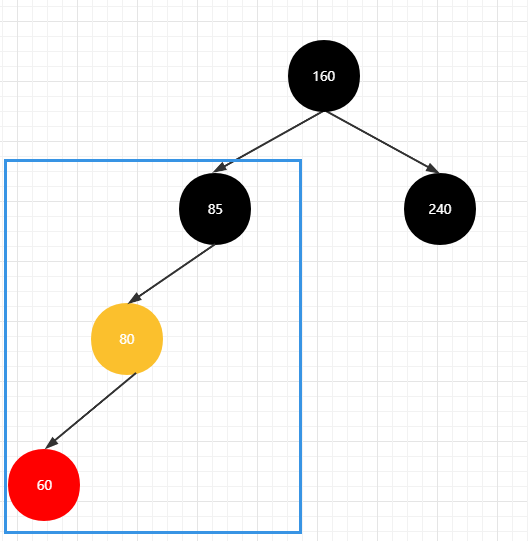
左右情况

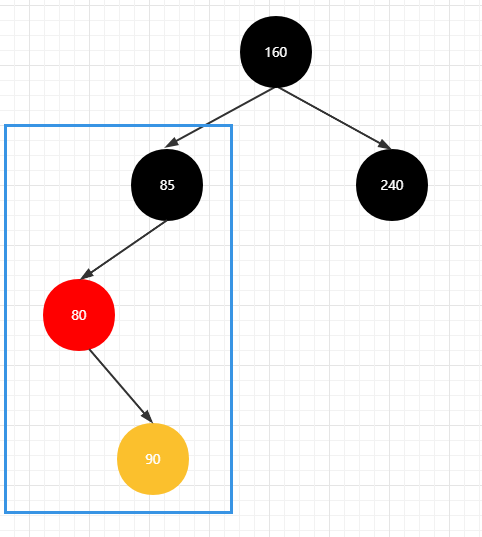
右左情况

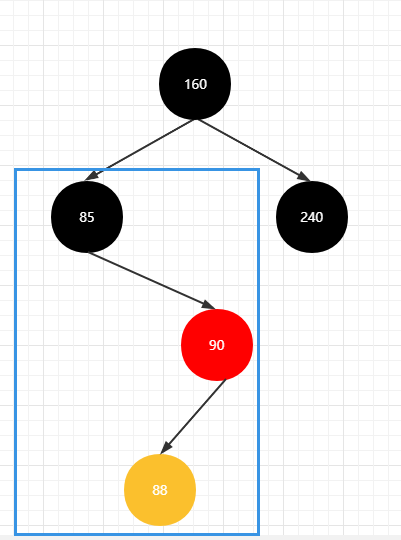
右右情况

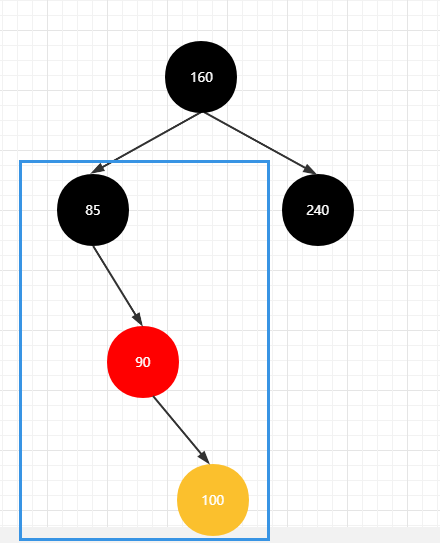
5.2 判断方向

若新插入节点的父亲节点在爷爷节点的左边，且新插入节点在父亲节点的左边，则为 左左情况

若新插入节点的父亲节点在爷爷节点的左边，且新插入节点在父亲节点的右边，则为 左右情况

若新插入节点的父亲节点在爷爷节点的右边，且新插入节点在父亲节点的左边，则为 右左情况

若新插入节点的父亲节点在爷爷节点的右边，且新插入节点在父亲节点的右边，则为 右右情况

代码实现

if ((parent->color == RED) && uncleColor == BLACK) {
	if ((parent == grandParent->left) && (newNode == parent->left)) {
        // 左左情况
        
    } else if ((parent == grandParent->left) && (newNode == parent->right)) {
        // 左右情况
        
    } else if ((parent == grandParent->right) && (newNode == parent->left)) {
        // 右左情况
        
    } else if ((parent == grandParent->right) && (newNode == parent->right)) {
        // 右右情况
    }
}

5.3 旋转图示

左左情况

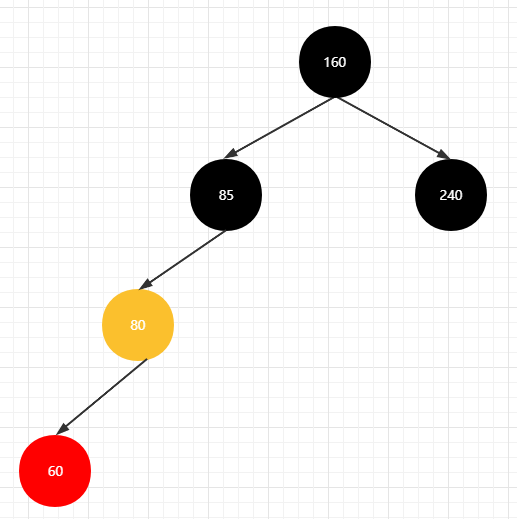
进行右旋操作

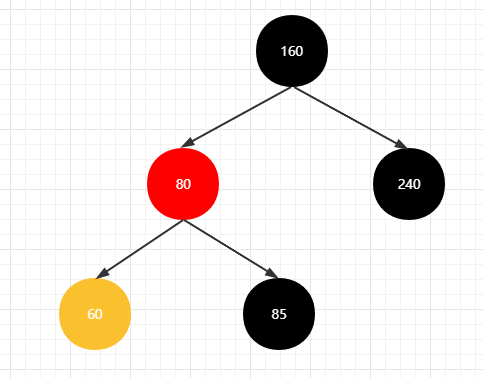
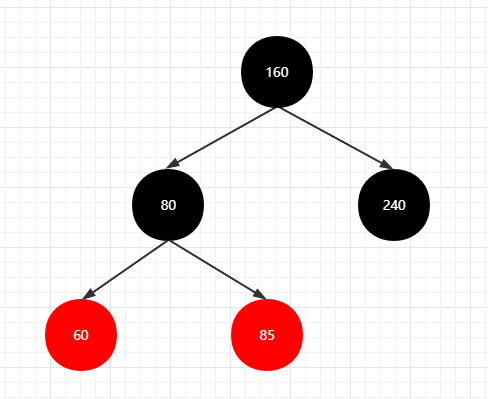
染色操作

将父亲节点(80)染成黑色，爷爷节点(85)染成红色, 当前节点(60)染成红色

左右情况

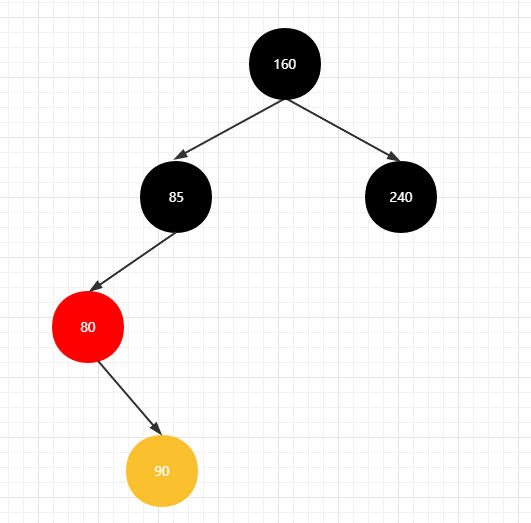
先进行左旋，将会变为【左左】情况一致

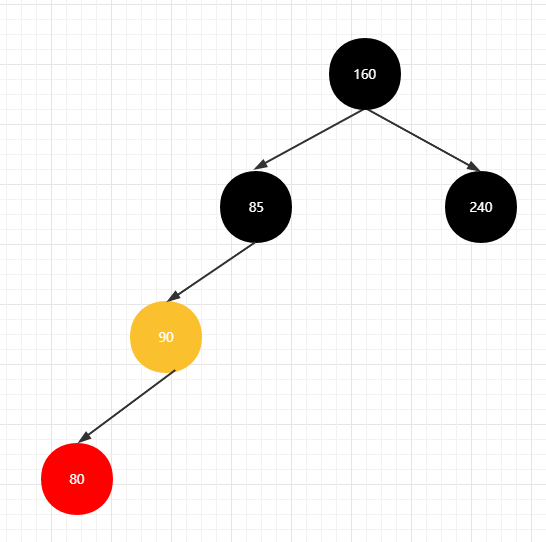
右左情况

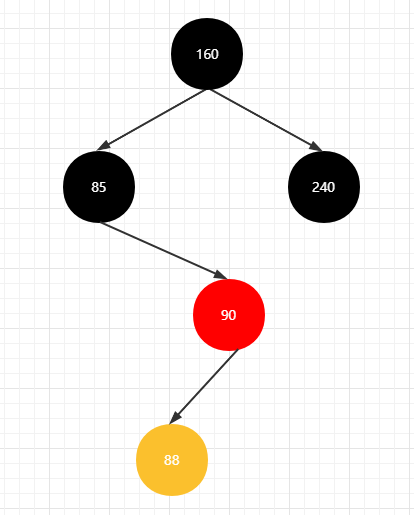
先进行右旋，将会变为【右右】情况一致

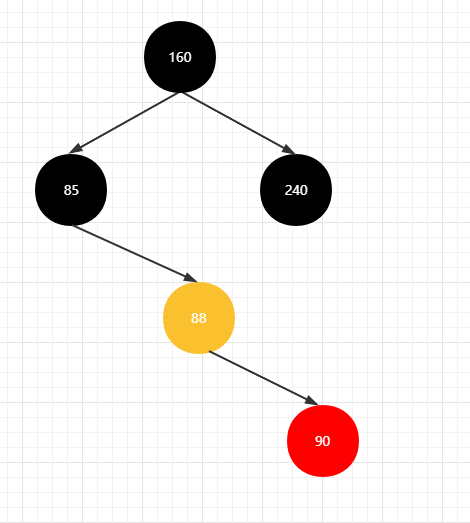
上图变得和即将讲述的【右右】情况类似了

右右情况

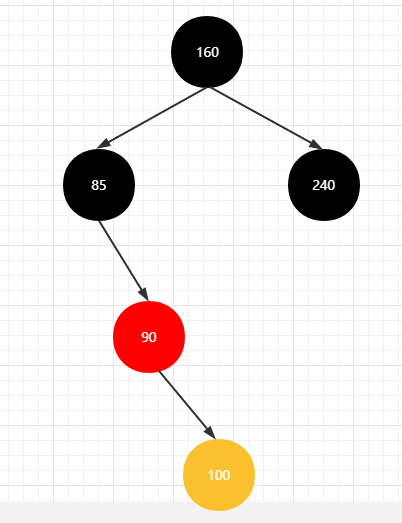
进行左旋操作

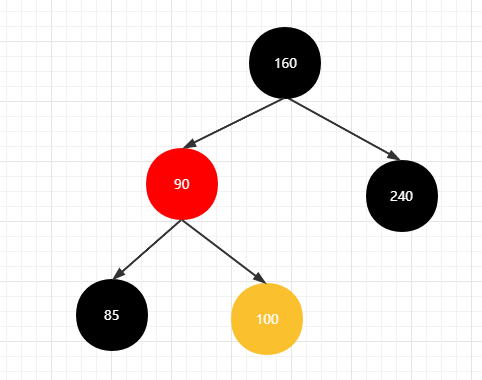
进行染色处理

将父亲节点(90)染成黑色，将爷爷节点(85)染成红色，当前节点(100)染成红色

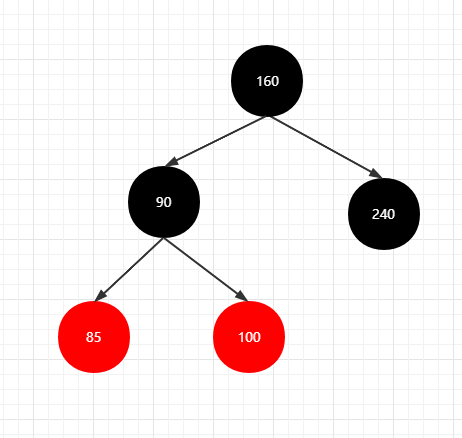
5.4 旋转代码实现

左左旋转

// 左左
if ((parent == grandParent->left) && (newNode == parent->left)) {
    grandParent->left = NULL;

    TreeNode *oldParentRight = parent->right;

    parent->right = grandParent;
    grandParent->left = oldParentRight;

    if ((*root) == grandParent) {
        (*root) = parent;
    } else {
        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
    }

    // 染色
    newNode->color = RED;
    grandParent->color = RED;
    parent->color = BLACK;
    //continue;
    break;
}

左右旋转

// 左右
if ((parent == grandParent->left) && (newNode == parent->right)) {
    grandParent->left = newNode;

    TreeNode *newNodeLeft = newNode->left;


    newNode->left = parent;
    parent->right = newNodeLeft;

    TreeNode *newNodeRight = newNode->right;
    newNode->right = grandParent;
    grandParent->left = newNodeRight;
    //newNode->left = parent;

    // 若要旋转的树是根节点
    if ((*root) == grandParent) {
        (*root) = newNode;
    } else {
        // 要旋转的树非根节点
        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
    }

    parent->color = RED;
    grandParent->color = RED;
    newNode->color = BLACK;
    //continue;
    break;
}

右左旋转

// 右左
if ((parent == grandParent->right) && (newNode == parent->left)) {
    parent->left = NULL;

    TreeNode *newNodeRight = newNode->right;
    newNode->right = parent;
    parent->left = newNodeRight;

    grandParent->right = newNode;

    TreeNode *newNodeLeft = newNode->left;
    newNode->left = grandParent;
    grandParent->right = newNodeLeft;


    // 要旋转的树是根节点
    if ((*root) == grandParent) {
        (*root) = newNode;

    } else {
        // 要旋转的树是非根节点
        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
    }

    // 染色
    newNode->color = BLACK;
    grandParent->color = RED;
    parent->color = RED;
    //continue;
    break;
}

右右旋转

if ((parent == grandParent->right) && (newNode == parent->right)) {
    grandParent->right = NULL;

    TreeNode *oldParentLeft = parent->left;
    parent->left = grandParent;
    grandParent->right = oldParentLeft;

    // 要旋转的树是根节点
    if ((*root) == grandParent) {
        (*root) = parent;

    } else {
        // 要旋转的树是非根节点
        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
    }

    // 染色
    grandParent->color = RED;
    newNode->color = RED;
    parent->color = BLACK;
    //continue;
    break;
}

整合代码插入修复函数

PTreeNode InsertFixup(PTreeNode *root,PTreeNode newNode) {

        TreeNode *parent = NULL; // 父亲节点
        TreeNode *grandParent = NULL; // 爷爷节点 
        TreeNode *greatGrandParent = NULL; // 祖爷爷节点
        TreeNode *uncle = NULL; // 叔叔节点
        int uncleColor = BLACK; // 叔叔节点颜色，默认为黑色

        while (true) {

                parent = grandParent = greatGrandParent = uncle = NULL;
                uncleColor = BLACK;

                // 寻找节点 父亲/爷爷祖爷爷节点
                TreeNode *tmp = (*root);
                while (tmp != NULL) {
                        if (newNode->data == tmp->data) {
                                break;
                        }
                        greatGrandParent = grandParent;
                        grandParent = parent;
                        parent = tmp;

                        (newNode->data > tmp->data) ? (tmp = tmp->right) : (tmp = tmp->left);
                }

                // 当前节点是根节点，染成黑色
                if (newNode == (*root)) {
                        printf("根节点，需要进行染色操作
");
                        (*root)->color = BLACK;
                }

                if (grandParent == NULL) return;

                // 获取叔叔节点
                (parent == grandParent->left) ? (uncle = grandParent->right) : (uncle = grandParent->left);

                // 获取叔叔节点颜色
                if (uncle != NULL) uncleColor = uncle->color;



                if ((parent->color == RED) && (uncleColor == RED)) {
                        // 父亲节点为红色，叔叔节点为红色，需要进行染色修复
                        printf("需要进行染色修复
");

                        parent->color = BLACK;
                        uncle->color = BLACK;
                        grandParent->color = RED;

                        newNode = grandParent;
                        continue;

                } else if((parent->color == RED) && uncleColor == BLACK) {
                        // 父节点为红色，叔叔节点为黑色，则需要进行旋转
                        printf("需要进行旋转修复
");
                        // 左左
                        if ((parent == grandParent->left) && (newNode == parent->left)) {
                                grandParent->left = NULL;

                                TreeNode *oldParentRight = parent->right;

                                parent->right = grandParent;
                                grandParent->left = oldParentRight;

                                if ((*root) == grandParent) {
                                        (*root) = parent;
                                } else {
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
                                }

                                // 染色
                                newNode->color = RED;
                                grandParent->color = RED;
                                parent->color = BLACK;
                                //continue;
                                break;
                        // 左右
                        } else if ((parent == grandParent->left) && (newNode == parent->right)) {
                                grandParent->left = newNode;

                                TreeNode *newNodeLeft = newNode->left;


                                newNode->left = parent;
                                parent->right = newNodeLeft;

                                TreeNode *newNodeRight = newNode->right;
                                newNode->right = grandParent;
                                grandParent->left = newNodeRight;
                                newNode->left = parent;

                                // 若要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = newNode;
                                } else {
                                        // 要旋转的树非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
                                }

                                parent->color = RED;
                                grandParent->color = RED;
                                newNode->color = BLACK;
                                //continue;
                                break;

                        // 右左
                        } else if ((parent == grandParent->right) && (newNode == parent->left)) {
                                parent->left = NULL;

                                TreeNode *newNodeRight = newNode->right;
                                newNode->right = parent;
                                parent->left = newNodeRight;

                                grandParent->right = newNode;

                                TreeNode *newNodeLeft = newNode->left;
                                newNode->left = grandParent;
                                grandParent->right = newNodeLeft;


                                // 要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = newNode;

                                } else {
                                        // 要旋转的树是非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
                                }

                                // 染色
                                newNode->color = BLACK;
                                grandParent->color = RED;
                                parent->color = RED;
                                //continue;
                                break;

                        // 右右
                        } else if ((parent == grandParent->right) && (newNode == parent->right)) {
                                grandParent->right = NULL;

                                TreeNode *oldParentLeft = parent->left;
                                parent->left = grandParent;
                                grandParent->right = oldParentLeft;

                                // 要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = parent;

                                } else {
                                        // 要旋转的树是非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
                                }

                                // 染色
                                grandParent->color = RED;
                                newNode->color = RED;
                                parent->color = BLACK;
                                //continue;
                                break;
                        }
                } else {
                        // 无需进行修复
                        printf("无需进行修复
");
                        break;
                }
        }
        return (*root);
}

6. 插入全部代码

引入搜索二叉树插入代码

# include <stdio.h>
# include <stdlib.h>
# include <stdbool.h>

# define RED 1
# define BLACK 0

typedef struct {
        int data; // 数据节点
        struct TreeNode *left; // 左子树
        struct TreeNode *right; // 右字树
        int color;  // 二叉树颜色，1: 红色 0:黑色

} TreeNode , *PTreeNode;

PTreeNode InsertFixup(PTreeNode *root,PTreeNode newNode) {

        TreeNode *parent = NULL; // 父亲节点
        TreeNode *grandParent = NULL; // 爷爷节点 
        TreeNode *greatGrandParent = NULL; // 祖爷爷节点
        TreeNode *uncle = NULL; // 叔叔节点
        int uncleColor = BLACK; // 叔叔节点颜色，默认为黑色

        while (true) {

                parent = grandParent = greatGrandParent = uncle = NULL;
                uncleColor = BLACK;

                // 寻找节点 父亲/爷爷祖爷爷节点
                TreeNode *tmp = (*root);
                while (tmp != NULL) {
                        if (newNode->data == tmp->data) {
                                break;
                        }
                        greatGrandParent = grandParent;
                        grandParent = parent;
                        parent = tmp;

                        (newNode->data > tmp->data) ? (tmp = tmp->right) : (tmp = tmp->left);
                }

                // 当前节点是根节点，染成黑色
                if (newNode == (*root)) {
                        printf("根节点，需要进行染色操作
");
                        (*root)->color = BLACK;
                }

                if (grandParent == NULL) return;

                // 获取叔叔节点
                (parent == grandParent->left) ? (uncle = grandParent->right) : (uncle = grandParent->left);

                // 获取叔叔节点颜色
                if (uncle != NULL) uncleColor = uncle->color;



                if ((parent->color == RED) && (uncleColor == RED)) {
                        // 父亲节点为红色，叔叔节点为红色，需要进行染色修复
                        printf("需要进行染色修复
");

                        parent->color = BLACK;
                        uncle->color = BLACK;
                        grandParent->color = RED;

                        newNode = grandParent;
                        continue;

                } else if((parent->color == RED) && uncleColor == BLACK) {
                        // 父节点为红色，叔叔节点为黑色，则需要进行旋转
                        printf("需要进行旋转修复
");
                        // 左左
                        if ((parent == grandParent->left) && (newNode == parent->left)) {
                                grandParent->left = NULL;

                                TreeNode *oldParentRight = parent->right;

                                parent->right = grandParent;
                                grandParent->left = oldParentRight;

                                if ((*root) == grandParent) {
                                        (*root) = parent;
                                } else {
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
                                }

                                // 染色
                                newNode->color = RED;
                                grandParent->color = RED;
                                parent->color = BLACK;
                                //continue;
                                break;
                        // 左右
                        } else if ((parent == grandParent->left) && (newNode == parent->right)) {
                                grandParent->left = newNode;

                                TreeNode *newNodeLeft = newNode->left;


                                newNode->left = parent;
                                parent->right = newNodeLeft;

                                TreeNode *newNodeRight = newNode->right;
                                newNode->right = grandParent;
                                grandParent->left = newNodeRight;
                                newNode->left = parent;

                                // 若要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = newNode;
                                } else {
                                        // 要旋转的树非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
                                }

                                parent->color = RED;
                                grandParent->color = RED;
                                newNode->color = BLACK;
                                //continue;
                                break;

                        // 右左
                        } else if ((parent == grandParent->right) && (newNode == parent->left)) {
                                parent->left = NULL;

                                TreeNode *newNodeRight = newNode->right;
                                newNode->right = parent;
                                parent->left = newNodeRight;

                                grandParent->right = newNode;

                                TreeNode *newNodeLeft = newNode->left;
                                newNode->left = grandParent;
                                grandParent->right = newNodeLeft;


                                // 要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = newNode;

                                } else {
                                        // 要旋转的树是非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = newNode) : (greatGrandParent->right = newNode);
                                }

                                // 染色
                                newNode->color = BLACK;
                                grandParent->color = RED;
                                parent->color = RED;
                                //continue;
                                break;

                        // 右右
                        } else if ((parent == grandParent->right) && (newNode == parent->right)) {
                                grandParent->right = NULL;

                                TreeNode *oldParentLeft = parent->left;
                                parent->left = grandParent;
                                grandParent->right = oldParentLeft;

                                // 要旋转的树是根节点
                                if ((*root) == grandParent) {
                                        (*root) = parent;

                                } else {
                                        // 要旋转的树是非根节点
                                        (greatGrandParent->left == grandParent) ? (greatGrandParent->left = parent) : (greatGrandParent->right = parent);
                                }

                                // 染色
                                grandParent->color = RED;
                                newNode->color = RED;
                                parent->color = BLACK;
                                //continue;
                                break;
                        }
                } else {
                        // 无需进行修复
                        printf("无需进行修复
");
                        break;
                }
        }
        return (*root);
}

PTreeNode Insert(PTreeNode *root,int data) {

        printf("插入数据: %d
",data);
        TreeNode *newNode = (TreeNode *)malloc(sizeof(TreeNode));
        newNode->data = data;
        newNode->color = RED; // 新增节点染成红色

        TreeNode *parent = NULL;
        TreeNode *grandParent = NULL;

        if (NULL == (*root)) {
                //printf("插入根节点
");
                newNode->color = BLACK; // 将头结点染成黑色
                return newNode;
        } else {
                TreeNode *tmp = (*root);
                while (tmp != NULL) {
                        //printf("插入查找值: %d
",tmp->data);
                        grandParent = parent;
                        parent = tmp;

                        if (data > tmp->data){
                                tmp = tmp->right;
                        } else if (data < tmp->data){
                                tmp = tmp->left;
                        } else {
                                printf("%d 该值已经存在
",data);
                        }
                }
                if (data > parent->data) {
                        parent->right = newNode;
                        //printf("parent data:%d newNode data:%d
",parent->data,newNode->data);
                } else {
                        parent->left = newNode;
                }
        }
        // 如果插入父节点是黑色，则保持不变
        if (parent->color == BLACK) return (*root);

        // 进行插入修复
        return InsertFixup(root,newNode); 
}


// 中序遍历
void Print2(TreeNode *root) {
        if (NULL == root) return;
        Print2(root->left);
        printf("[颜色:%s  数据:%d]	",(root->color == RED) ? ("红"):("黑") ,root->data);
        Print2(root->right);
}
// 前序遍历
void Print1(TreeNode *root) {
        if (NULL == root) return;
        printf("[颜色:%s  数据:%d]	",(root->color == RED) ? ("红"):("黑") ,root->data);
        Print1(root->left);
        Print1(root->right);
}

int main() {
        TreeNode *root = NULL;

        int num[] = {10,6,11,4,8,20,19,26,17,23,35,40,55,32,231};

        int i;
        for (i=0;i<sizeof(num)/sizeof(int);i++) {
                root = Insert(&root,num[i]);
        }

        printf("
");
        Print1(root);
        printf("
");

        return 0;
}

执行结果

# gcc RedBlackTreeInsert.c -w -g
# ./a.out 
插入数据: 10
插入数据: 6
插入数据: 11
插入数据: 4
需要进行染色修复
根节点，需要进行染色操作
插入数据: 8
插入数据: 20
插入数据: 19
需要进行旋转修复
插入数据: 26
需要进行染色修复
插入数据: 17
插入数据: 23
需要进行旋转修复
插入数据: 35
需要进行染色修复
需要进行旋转修复
插入数据: 40
需要进行旋转修复
插入数据: 55
需要进行染色修复
需要进行染色修复
根节点，需要进行染色操作
插入数据: 32
插入数据: 231
需要进行旋转修复

[颜色:黑  数据:19]      [颜色:黑  数据:10]      [颜色:黑  数据:6]       [颜色:红  数据:4]       [颜色:红  数据:8]       [颜色:黑  数据:11]  [颜色:红  数据:17]      [颜色:黑  数据:23]      [颜色:黑  数据:20]      [颜色:红  数据:35]      [颜色:黑  数据:26]      [颜色:红  数据:32] [颜色:黑  数据:55]      [颜色:红  数据:40]      [颜色:红  数据:231]
#

欢迎转发！请保留源地址: https://www.cnblogs.com/NoneID

查看全文

相关阅读:
常用词汇短语
 Java中的数据结构
 Java中的设计模式
 .NET中的编译、程序调用
 常用口语
 0. Angular框架原理
 茶叶
 NPOI自定义单元格背景颜色
 ASP.NET MVC添加Action就找不到
 navicat for mysql 导入SQL Server显示中文乱码解决办法

原文地址：https://www.cnblogs.com/NoneID/p/15441092.html