LIFTOVI
Solitaire has N elevators. Each elevator are connecting exactly two floors and it does not stop on the
floors between that two floors. The speed of all the elevators are the same, 5 seconds to pass one
floor.
On the beginning, each elevator is in its lower position and they are starting cruising to the upper floor.
After some elevator come to its upper position, it immediatly starts to go back to its lower position,
and so on...
Mirko is on the first (the lowest) floor and he wants as quick as possible come to the top of the
solitaire. He can change elevators only on the floors that are common to both elevators, and if the
other elevator is in that moment on that floor, that change does not take any time.
Write a program that will calculate minimal time in which Mirko can get to the top of the solitaire.
Input data
In the first line of the input file there are two integers K and N, separated with space, number of floors
in solitaire and number of elevators, 2 ≤ K ≤ 1000, 1 ≤ N ≤ 50000.
In each of the next N lines there are description of one elevator, two integers A and B, separated with
space, 1 ≤ A < B ≤ K, means that elevator is travelling between floors A and B.
There are no two different elevators that travels between same floors.
Note: input data will guarantee that solution will always exists.
Output data
In the only line of output file write minimal time (in seconds) from the text above.
Examples
liftovi.in
10 4
1 5
5 10
5 7
7 10
liftovi.out
45
liftovi.in
10 3
1 5
3 5
3 10
liftovi.out
105
liftovi.in
20 5
1 7
7 20
4 7
4 10
10 20
liftovi.out
150
分析
首先我们要明确这道题目的基本方法,因为这道题目求最短的时间(我们将其理解为最短路程的问题),最短路程一定是从起点一层层向前推,首先找到的符合条件的答案是最有答案。那么我们就确定下来,这道题用基于广搜的SPFA。
对于模板SPFA,这道题最大的一个改变就是路程的量变成了时间,所以我们关键在于如何分析写出时间的公式。对于当前状态(已用时间,所在楼层),我们要将其从队列中弹出,然后枚举与当前楼层相连的所有电梯,分成两种情况。接下来电梯下行,和接下来电梯上行两种情况。对于上行,我们有公式:
dis = f[a[x][1]]+(y/2+y-f[a[x][1]]%y)%y+y/2;
也可以理解为:
SUCC = PRE + (y/2+y-PRE%y)%y + y/2;
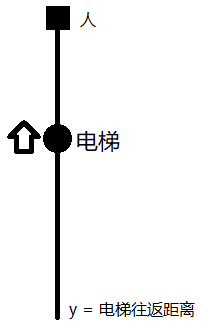
相对的,电梯下行的公式就是:
dis = f[a[x][0]]+(y-f[a[x][0]]%y)%y+y/2;
这样一来,程序就是模板SPFA了。
程序
1 #include<bits/stdc++.h> 2 using namespace std; 3 int n, m, i, j, t, k, s, f[1005], a[50005][2]; 4 vector<int> vec[1005]; 5 bool inq[1005]; 6 void SPFA() 7 { 8 memset(f,0x3F3F3F3F,sizeof(f)); 9 f[1]=0; 10 queue<int> Q; 11 Q.push(1); 12 while (!Q.empty()) 13 { 14 int t = Q.front(); 15 Q.pop(); 16 inq[t]=0; 17 for (int i=0;i<vec[t].size();++i) 18 { 19 int x = vec[t][i], y = (a[x][1]-a[x][0])*2*5; 20 if (t == a[x][0]) 21 { 22 int dis = f[a[x][0]]+(y-f[a[x][0]]%y)%y+y/2; 23 if (f[a[x][1]]>dis) 24 { 25 f[a[x][1]]=dis; 26 if (!inq[a[x][1]]) 27 { 28 inq[a[x][1]]=1; 29 Q.push(a[x][1]); 30 } 31 } 32 } 33 else 34 { 35 int dis=f[a[x][1]]+(y/2+y-f[a[x][1]]%y)%y+y/2; 36 if (f[a[x][0]]>dis) 37 { 38 f[a[x][0]]=dis; 39 if (!inq[a[x][0]]) 40 { 41 inq[a[x][0]]=1; 42 Q.push(a[x][0]); 43 } 44 } 45 } 46 } 47 } 48 } 49 50 int main() 51 { 52 freopen("liftovi.in","r",stdin); 53 freopen("liftovi.out","w",stdout); 54 scanf("%d%d",&n,&m); 55 for (i=1;i<=m;++i) 56 { 57 scanf("%d%d",&a[i][0],&a[i][1]); 58 vec[a[i][0]].push_back(i); 59 vec[a[i][1]].push_back(i); 60 } 61 SPFA(); 62 printf("%d ",f[n]); 63 return 0; 64 }