Programming Pearls笔记之三
Programming Pearls笔记之三
这里是编程珠玑(Programming Pearls)第三部分(后五个专栏)的笔记.
1 Partition
快速排序最关键的一步是Partition,将一个元素放在正确的位置,它前面的元素都小于它,它后面的元素都不小于它.
1.1 Nico Lomuto的方法
对于一个值t,将数组分成两部分,一部分小于t,一部分大于等于t.如图:

图一
相应算法为:
m = a-1 for i = [a, b] if x[i] < t swap(++m, i)
将x[l]作为数值t,如下图:
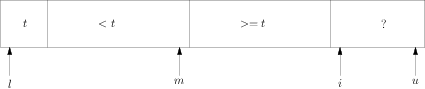
图二
这时的a即l+1.b即u.算法终结时的状态是:
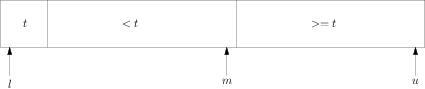
图三
最后还要交换x[l]和x[m],状态为:
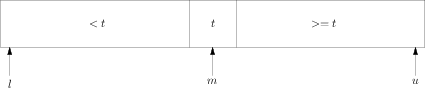
图四
1.2 一些改进
Lomuto的方法有一点问题,就是当重复元素较多时效率会较差.对于n个元素全部相同的极端情况,时间复杂度变为O(n).下面的方案会较好:

图五
这时算法是:
t = x[l]; i = l; j = u+1
loop
do i++ while i <=u && x[i] < t
do j-- while x[j] > t
if i > j
break
swap(i, j)
swap(l, j)
当所有元素都相等时.这个算法会交换相等的元素,这是不必要的.但它会将数组从正中间分成两部分,所以时间复杂度是O(n log n).这也是严、吴版《数据结构》课本上给出的算法.
另外为了取得较好的平均时间复杂度,可以引用随机数:swap(l,randint(l,u)).即随机将数组中的一个元素跟x[l],用它作为t.
还有就是当u-l较小时,快速排序效率并不好,这时可以设置一个临界值,当u-l小于这个值时不再进行Partition操作而是直接返回,这样最终结果虽然不是有序的,但却是大致有序的,这时可以再用插入排序处理一遍.
2 R.Sedgewick的优化
- 问题
通过让x[l]作为哨兵元素,去掉Lomuto的算法中循环后面的那个swap语句.
可以说这个改进没什么用处,因为只是少了一个交换语句,但这个问题很有意思.
- 解答
Bob Sedgewick发现可以修改Lmuto的方案,从右往左处理数组元素,这样x[l]就可以作为一个哨兵元素,数组状态如下:
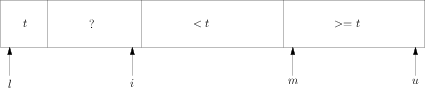
图六
算法伪代码是:
m = u+1 for (i = u; i >= l; i--) if x[i] >= t swap(--m, i)
当算法处理完后x[m]=t,因此也就不用再交换了.利用这个方案Sedgewick还可以省掉循环中的一个判断语句:
m = i = u+1 do while x[--i] < t ; swap(--m, i) while i != l
3 第k小元素
- 问题
查找数组x[0..n-1]中第k小元素,要求时间复杂度为O(n),允许改变数组中元素顺序.
- 解答
这个很简单,只是对Partition稍作修改.C.A.R.Hoare的算法:
void select1(l, u, k) pre l <= k <= u post x[l..k-1] <= x[k] <= x[k+1..u] if l >= u return swap(l, randint(l, u)) t = x[l]; i = l; j = u+1 loop do i++; while i <= u && x[i] < t do j--; while x[j] >t if i > j break temp = x[i]; x[i] = x[j]; x[j] = temp swap(l, j) if j < k select1(j+1, u, k) else if j > k select1(l, j-1, k)
4 抽样问题
从0..n-1中等概率随机选取m(m<n)个并升序输出,要求不能有重复数值.
4.1 Knuth的方法S
select = m remaining = n for i = [0, n) if (bigrand() % remaining) < select print i select-- remaining--
其中的bigrand()是产生一个随机整数.
巧妙之处是直接升序考查,输出,不用再排序了.
4.2 Knuth的方法P
先将数组随机打乱,然后将前m个排序.
for i = [0, n) swap(i, randint(i, n-1)) sort(x, x+m) for i = [0, m) printf x[i]
Ashley Shepherd和Alex Woronow发现只要对前m个进行打乱操作就行了:
void genshuf(int m, int n) { int i, j; int *x = new int[n]; for (i = 0; i < n; i++) x[i] = i; for (i = 0; i < m; i++) { j = randint(i, n-1); int t = x[i]; x[i] = x[j]; x[j] = t; } sort(x, x+m); for (i = 0; i < m; i++) cout << x[i] <<"\n"; }
4.3 m接近n的情况
- 问题
当m接近n时,容易想到的解法是找出要舍弃的n-m个,然后剩下的就是要选取的.然而此处的问题是:
当m接近n的时候,基于集合的方法会产生很多重复的随机数值.要求设计一种算法,即使在最坏的情况下也只需要产生m个随机数.
问题中基于集合的算法如下:
initialize set S to empty size = 0 while size < m do t = bigrand() % n if t is not in S insert t into S size++ print the elements of S in sorted orrder
- 解答
下面是Bob Floyd的算法:
void genfloyd(int m, int n) { set<int S; set<int>::iterator i; for (int j = n-m; j < n; j++) { int t = bigrand() % (j+1); if (S.find(t) == S.end()) S.insert(t); // t not in S else S.insert(j); // t in S } for (i = S.begin(); i != S.end(); ++i) cout << *i <<"\n"; }
4.4 n未知时的情况
- 问题
读取一篇文章,等概率地随机输出其中的一行.
这里n在读完文章之前未知,m=1.
- 解答
可以先选中第一行,当读入第二行时,再以1/2的概率选中第二行,读入第三行时再以1/3的概率选中第三行...最后输出选中行.
i = 0 while more input lines with probability 1.0/++i choice = this input line print choice这个算法可以用数学归纳法作下不太正式的证明:选中每一行的概率都是1/n.
- 当n=1时,以100%的概率选中第一行,满足要求.
- 假设当n=k时,满足要求.则当输入第k+1行时,选中第k+1行的概率为1/(k+1).这一事件对于前k行的影响是相同的,又因为原来(读入第k+1行之前)选中前k行中任一行的概率是相同的,所以读入第k+1行之后选中前k行中任一行的概率也是相同的.这时选中前k行的概率是1-1/(k+1).故选中前k行任一行的概率也是1/(k+1).所以当n=k+1时,也符合要求.
- 综上,算法满足要求.
- 笔记
上面的问题是m=1时的情况,当m>1时,可以先确定前m行为已经选中,然后对于后面的第i行(m<i<n)以m/i的概率选中它,并随机替换掉已经选中的m行中的一行,这时要产生两个随机数,一个用来确定是否选中该行,一个用来确定换掉m行中的哪一行,可以将这两步操作合并成一步,只用求一个随机数,算法如下:1
i = 0 while more input lines if i < m x[i++] = this input line else t = bigrand() % (++i) if t < m x[t] = this input line for i = [0, m) printf x[i]
算法中的行数i是从0开始的,这样利用bigrand()求出的t,就不用再加1了.根据上面的算法也可以得出m接近n的情况的另外一个较好的解,因此m比较接近n,因此n-m较小,此时只用产生比较少的n-m个随机数即可:
for i = [0, m) x[i] = i for i = [m, n) t = bigrand() % (i+1) if (t < m) x[t] = i for i = [0, m) print x[i]
5 最长重复子串
- 问题
求出在一个字符串中重复出现的子串,比如对于字符串"banana",字符串"ana"是最长重复子串,因为出现了两次:b ana na和ban ana .
- 解答
仍以字符串"banana"为例.可以先建一个指针数组a,a[0]指向整个字符串,a[1]指向以a开头的后缀,a[2]指向以n开头的后缀:
- a[0]: banana
- a[1]: anana
- a[2]: nana
- a[3]: ana
- a[4]: na
- a[5]: a
然后对这个指针数组调用qsort()进行排序就行了.比较函数是对元素指向的字符串的大小进行比较.在本例中,结果为:
- a[0]: a
- a[1]: ana
- a[2]: anana
- a[3]: banana
- a[4]: na
- a[5]: nana
最后只要比较排序后相信的子串,就可以得出最长重复子串,即"aba".