放牛奶的冰箱
时间限制: 1 Sec 内存限制: 256 MB
[提交] [状态]
题目描述
冬冬在古子城购买了一台冰箱,冰箱内部可以表示为高度为h,深度为1,宽度为2的矩阵,最初冰箱底部只有一个架子,但冬冬可以在任何一个格子顶部放隔板,隔板的宽为2,不占用任何空间,将冰箱内部分隔成上、下两部分。
冬冬有n瓶牛奶要按顺序放入冰箱里。第i瓶牛奶的高度是ai,深度和宽度均为1。如果架子上方的相应空间至少与瓶子一样高,他可以在一个架子上放一瓶牛奶,他不能将两瓶牛奶叠在一起(如果它们之间没有架子)。
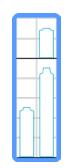
上图为一个高为7,宽为2的冰箱,在高为5的位置放了一块隔板,冰箱内放了高3瓶牛奶,高度为3、5、2。
冬冬按顺序将牛奶往冰箱里放,他最多能往冰箱里放k瓶牛奶,他想知道k的值为多少?
输入
第一行包含两个整数n和h(1≤n≤106,1≤h≤106)表示牛奶的数量和冰箱的高度。
第二行包含n个整数a1,a2,…,an(1≤ai≤min(100,h))表示第i瓶牛奶的高度。
输出
输出k的值。
样例输入 Copy
【样例1】
5 7
2 3 5 4 1
【样例2】
10 10
9 1 1 1 1 1 1 1 1 1
【样例3】
5 10
3 1 4 2 4
样例输出 Copy
【样例1】
3
【样例2】
4
【样例3】
5
提示

对于60%的数据,1≤n≤1000,1≤h≤1000,1≤ai≤min(100,h)。
对于100%的数据,1≤n≤106,1≤h≤106,1≤ai≤min(100,h)。
思路:
这题太可了!
比赛时没想出来是因为思维被限制了,一直在考虑对于一瓶新的牛奶是另开辟一个隔板还是在原来有牛奶的旁边放,还以为是dp~
其实可以二分做的,因为是按顺序放的,你放多少瓶牛奶和这些牛奶能否放得下一定是具有单调性的。比如,前4瓶牛奶放不下,那么前5瓶牛奶一定也放不下。
接下来就考虑check函数的写法,我们假设的是前mid瓶牛奶都可以放得下,那么在放的过程中一定是取一个最优解,如何才是最优解呢?
我们把前mid瓶牛奶从小到大排序后,因为两个一组,最优解一定是每一组的第二个的和。
即
for(int i=2;i<=cnt;i+=2){
tmp-=b[i];
if(tmp<0) return 0;
}
但是如果是奇数的话,那么最后一个牛奶的高度就没有被计算上,所以我又改成了这样:
for(int i=2;i<=cnt;i+=2){
tmp-=b[i];
if(tmp<0) return 0;
}
if(cnt%2) tmp-=b[cnt];
这样就会忽略一个问题,在有些情况下,这种计算方式并不是最优的。
随便举个栗子:
假设当前需要check的牛奶的值分别是1,2,3,4,5
如果按这种方式,所需要的高度x=2+4+5=11;
但是,如果我们把4和5分到一组,3和4分到一组,1自己一组,所需高度就变成了5+3+1=9;
所以:在check函数中,要根据个数的奇偶决定放置方式~(妙啊)
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline void read(ll &x){
ll s = 0, w = 1; char ch = getchar();
while(ch < '0' || ch > '9'){ if(ch == '-') w = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
x = s*w;
}
const int maxn=1e6+100;
ll a[maxn],n,h,b[maxn];
bool check(ll x){
int cnt=0;
for(ll i=1;i<=x;i++)
b[++cnt]=a[i];
sort(b+1,b+cnt+1);///从小到大
ll tmp=h;
if(cnt%2==0){
for(int i=2;i<=cnt;i+=2){
tmp-=b[i];
if(tmp<0) return 0;
}
return 1;
}
else{
tmp=h;
for(int i=cnt;i>=1;i-=2){
tmp-=b[i];
if(tmp<0) return 0;
}
return 1;
}
}
int main(){
read(n);read(h);
ll sum=0;
for(ll i=1;i<=n;i++) read(a[i]),sum+=a[i];
if(sum<h){
printf("%lld
",n);
}
ll l=0,r=n,res;
while(l<=r){
ll mid=(l+r)>>1;
if(check(mid)) l=mid+1,res=mid;
else r=mid-1;
}
printf("%lld
",res);
return 0;
}