二分是一个很高贵的方法。(语出实验室某大佬)
我觉得也是,二分是一种巧妙地暴力。
二分
二分法在一个单调有序的集合或函数中查找一个解,每次分为左右两部分,判断解在哪个部分中并调整上下界,直到找到目标元素,每次二分后都将舍弃一半的查找空间,因此效率很高。
若求解的问题的定义域为整数域,对于长度为N的求解区间,算法需要logn次来确定出分界点。
对于定义域在实数域上的问题,可以类似于上面的方法,判断R-L的精度是否达到要求,即R-L>=eps。
如果我们指定二分的次数t,那么对于初始的求解区间长度L,算法结束后的r-l值会为L/2^t。
二分算法的复杂度O(二分次数*单次判定复杂度)。
(以上来自ppt)有点枯燥的干货
简单总结如下:
1.一般二分适用的题目都具有明显的单调性
2.二分的边界很重要
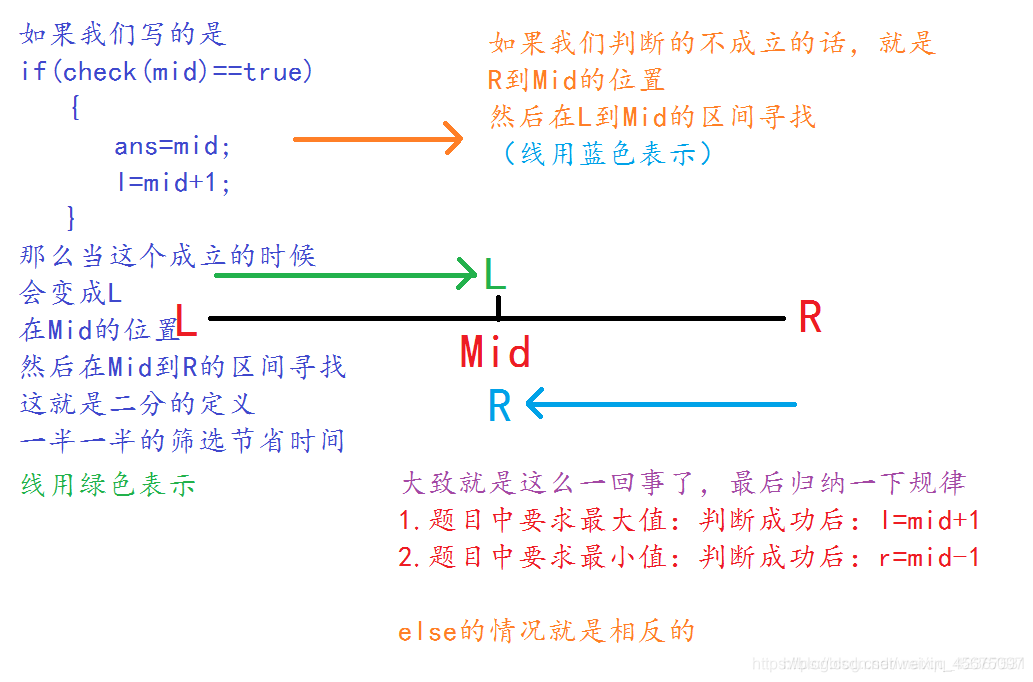
最后放一张大佬总结的图,模板不重要,理解二分的含义才是最重要的叭
例题~[愤怒的牛]
题目描述
农夫约翰建造了一座有n间牛舍的小屋,牛舍排在一条直线上,第i间牛舍在xi的位置,但是约翰的m头牛对小屋很不满意,因此经常互相攻击。约翰为了防止牛之间互相伤害,因此决定把每头牛都放在离其它牛尽可能远的牛舍。也就是要最大化最近的两头牛之间的距离。
牛们并不喜欢这种布局,而且几头牛放在一个隔间里,它们就要发生争斗。为了不让牛互相伤害。John决定自己给牛分配隔间,使任意两头牛之间的最小距离尽可能的大,那么,这个最大的最小距离是多少呢?
输入
第一行用空格分隔的两个整数n和m;
第二行为n个用空格隔开的整数,表示位置xi。
输出
输出仅一个整数,表示最大的最小距离值。
样例输入 Copy
5 3
1 2 8 4 9
样例输出 Copy
3
提示
把牛放在1,4,8这样最小距离是3
2≤n≤105 , 0≤xi≤109, 2≤m≤n
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+7;
int a[N],n,m;
bool check(int x){
int t=a[0];
int cnt=1;//表示当前的间距能够放下多少头牛
for(int i=1;i<n;i++)
if(a[i]-t>=x){//如果距离大于这个间距,更新下一个牛舍的位置
cnt++;
t=a[i];
if(cnt>=m) return true;
}
return false;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
sort(a,a+n);
//二分答案进行check,看当前mid是否满足答案
//根据题意 距离的边界是0到两头牛的最远距离
int l=0,r=a[n-1]-a[0];
int ans;
while(l<=r){
int mid=l+r>>1;
当前能够放下的牛大于等于m,记录下当前mid值,并试探再大一点的距离(即右半段区间的是否符合题意)
if(check(mid)) l=mid+1,ans=mid;
//当前不能放下m头牛 答案肯定在左半段区间
else r=mid-1;
}
cout<<r<<endl;
return 0;
}
三分
三分法适用于求解凸性函数的极值问题,二次函数就是一个典型的单峰函数。
三分法与二分法一样,它会不断缩小答案所在的求解区间。二分法缩短区间利用的原理是函数的单调性,而三分法利用的则是函数的单峰性。
设当前求解的区间为[l,r],令m1=l+(r-l)/3,m2=r-(r-l)/3,接着我们计算这两个点的函数值f(m1),f(m2),之后我们将两点中函数值更优的那个点称为好点(若计算最大值,则更大的那个点就为好点,计算最小值同理),而函数值较差的那个点称为坏点。
我们可以证明,最优点与好点会在坏点同侧。例如,f(m1)>f(m2),则是m1好点而m2是坏点,因此最后的最优点会与m1一起在m2的左侧,即我们的求解区间由变为了[l,m2]。因此根据这个结论我们可以不停缩短求解区间,直至可以得出近似解。
注意,我们在介绍单峰函数时特别强调了“严格”单调性。
若在三分过程中遇到 f(m1) = f(m2),当函数严格单调时,令 l = m1或 r = m2均可。如果函数不严格单调,即在函数中存在一段值相等的部分,那么我们无法判断定义域的左右边界如何缩小,三分法就不再适用。
没错,又是枯燥的干货
大体思路如下:
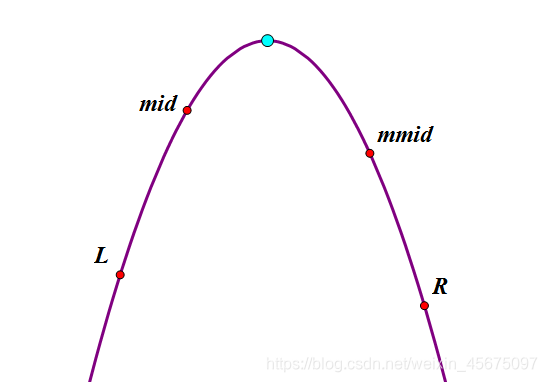
如图所示,已知左右端点L、R,要求找到白点的位置。
思路:通过不断缩小 [L,R] 的范围,无限逼近白点。
做法:先取 [L,R] 的中点 mid,再取 [mid,R] 的中点 mmid,通过比较 f(mid) 与 f(mmid) 的大小来缩小范围。
当最后 L=R-1 时,再比较下这两个点的值,我们就找到了答案。
1、当 f(mid) > f(mmid) 的时候,我们可以断定 mmid 一定在白点的右边。
反证法:假设 mmid 在白点的左边,则 mid 也一定在白点的左边,又由 f(mid) > f(mmid) 可推出 mmid < mid,与已知矛盾,故假设不成立。
所以,此时可以将 R = mmid 来缩小范围。
2、当 f(mid) < f(mmid) 的时候,我们可以断定 mid 一定在白点的左边。
反证法:假设 mid 在白点的右边,则 mmid 也一定在白点的右边,又由 f(mid) < f(mmid) 可推出 mid > mmid,与已知矛盾,故假设不成立。
同理,此时可以将 L = mid 来缩小范围。
例题
曲线
题目描述
明明做作业的时候遇到了n个二次函数Si(x)=ax2+bx+c,他突发奇想设计了一个新的函数F(x)=max{Si(x)},i=1…n。
明明现在想求这个函数在[0,1000]的最小值,要求精确到小数点后四位,四舍五入。
输入
输入包含T组数据,每组第一行一个整数n;
接下来n行,每行3个整数a,b,c,用来表示每个二次函数的3个系数。注意:二次函数有可能退化成一次。
输出
每组数据输出一行,表示新函数 F(x)的在区间 [0,1000]上的最小值。精确到小数点后四位,四舍五入。
样例输入 Copy
2
1
2 0 0
2
2 0 0
2 -4 2
样例输出 Copy
0.0000
0.5000
提示
对于50%的数据,1≤n≤100;
对于100%的数据,1≤T≤10,1≤n≤105,0≤a≤100,0≤∣b∣≤5000,0≤∣c∣≤5000。
#pragma GCC optimize(2)
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
typedef long long ll;
using namespace std;
const int N=1e6+7;
int a[N],b[N],c[N],n;
//三分的目的只是缩小区间来找,还是需要遍历一遍的
double check(double x){
double minn=-inf;
for(int i=1;i<=n;i++)
minn=max(minn,a[i]*x*x+b[i]*x+c[i]);
return minn;
}
int main(){
int t;
cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i]>>b[i]>>c[i];
//边界按照题目描述
double l=0,r=1000;
//这题精度很玄学,一般1e-8就可以,这题要1e-9以下,还是比较高的了
while(r-l>=1e-10){
double mid1=l+(r-l)/3,mid2=r-(r-l)/3;
//左边比右边大,小的值在右边,去右边找
if(check(mid1)>check(mid2)) l=mid1;
//去左边
else r=mid2;
}
//还是要再判断一次
printf("%.4lf
",check(l));
}
return 0;
}
三分真是个神奇的东西~
最后还是放一波模板叭 虽然自己不怎么用 (出自yxc大佬)
整数二分
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
参考博客:#10013. 「一本通 1.2 例 3」曲线_Lop-CSDN博客
#10012. 「一本通 1.2 例 2」Best Cow Fences_Lop-CSDN博客
【信息学奥赛一本通 提高组】第二章 二分与三分