CF232C Doe Graphs(分治)

传送门

题意:D(0)是只有一个编号为1的结点的图.D(1)是只有两个编号分别为1和2的点与一条连接这两个点的边的图.D(n)以如下方法构造:将D(n-2)中所有点的编号加上|D(n-1)|(即第n-1个图中的点数,或者说是最大的点的编号),在点|D(n-1)|与点|D(n-1)|+1之间连边.在点|D(n-1)|+1与点1之间连边.现在已经构造出了D(n)(n≤100),她会询问m次在这张图中a,b两点间的最短路.

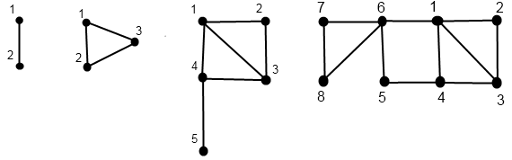
以上四幅图,分别表示D(1),D(2),D(3),D(4).

分析:真的被这道题搞死了,理解题意就耗尽了那一丢丢智商.首先,由图的生成方法可知,每张图的点数之间的关系满足斐波那契数列,所以可以直接根据公式递推出第n张图中点的个数.然后因为n<=100,而每一次询问的a,b的编号最大才(10^{16}),斐波那契数列的第100项已经远远大于(10^{16}),所以我下面的程序中读入n后,让n与80取min.

注意到对于n≥2的情形,|D(n−1)|+1是原图D(n)的一个割点(如上图,显然D(2)每个点都是割点,D(3)的割点是|D(2)|+1=4,D(4)的割点是|D(3)|+1=6).这个割点将D(n−1)和D(n−2)连接起来.相当于把D(n)拆成两张图来看,编号比割点小的点在子图D(n-1)中,编号比割点大的点在子图D(n-2)中.割点属于子图D(n-2)中

对于一个询问(a,b,n),我们不妨设a<b.设dis(a,b,n)为a到b在D(n)中的最短路,则有三种情况(如果看不懂式子,可以考虑直接结合图看代码,我写代码注释写了一个小时左右)

1、a ≤ |D(n − 1)|, b > |D(n − 1)|:

如上图所示,即a点在子图D(n−1)中,b点在子图D(n−2)中,所以a到b的最短路必定经过了割点|D(n−1)|+1,所以可以把最短路拆成两部分a到|D(n−1)|+1的最短路和|D(n−1)|+1到b的最短路.这两个部分每部分又可以化为更小图中的最短路,即子问题.

dis(a,b,n)=dis(a,|D(n−1)|+1,n)+dis(|D(n−1)|+1,b,n)= min{dis(1,a,n−1),dis(a,|D(n −1)|,n−1)}+dis(1,b−|D(n−1)|,n−2)+1

2、a, b > |D(n − 1)|:

这个没有图...即a和b都在子图D(n−2)中,所以a到b的最短路可能经过割点|D(n−1)|+1,但一定不会经过子图D(n−1).

dis(a,b,n)=dis(a−|D(n−1)|,b−|D(n−1)|,n−2)

3、a, b ≤ |D(n − 1)|:

如上图所示，即a和b都在子图D(n−1)中.所以除了割点|D(n − 1)|+1,最短路不可能用到D(n−2)中的其它点.所以只需考虑在D(n−1)的基础上新加入一条边(1,|D(n−1)|),长度为2(即图中的红色边).再求最短路即可.

dis(a,b,n)=min{dis(a,b,n−1), min{dis(1,a,n−1)+dis(b,|D(n − 1)|, n−1),dis(1,b,n−1)+dis(a,|D(n−1)|,n−1)}+ 2}

当n很大时,上面这种做法仍然会超时.考虑是否能预处理一些东西.对于每一张图,我们把编号最小的点(即点1),称作这张图的起点,把编号最大的点称作这张图的终点.所以,对于图D[n],它的起点1在它的子图D[n-1]中,它的终点在它的子图D[n-2]中.我们可以预处理出我们要询问的两个点a,b,在它们各自的所属子图中分别到起点1和终点的最短距离.

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN=1e3+5;
int n,m;
LL d[MAXN],g[MAXN];
LL a1[MAXN],a2[MAXN],b1[MAXN],b2[MAXN];
//当前处理的点是x,当前在图d[n]中
//c1[i],c2[i]分别记录点x在图d[i]中到起点和终点的距离
//对于图d[i],起点是1,终点是|d[i]|
void work(LL x,LL n,LL c1[],LL c2[]){
    if(n==0){
		c1[n]=c2[n]=0;
		return;
    }
//递归边界1
//在d[0]中,只有一个点,所以x到起点和终点的距离都是0
    if(n==1){
		c1[n]=(x==2);c2[n]=(x==1);
		return;
    }
//递归边界2
//在d[1]中,只有两个点1和2,
//若x=2,则x到起点1的距离是1,到终点2的距离是0;
//若x=1,则x到终点2的距离是1,到起点1的距离是0.
    if(x<=d[n-1]){//如果x在d[n]的子图d[n-1]中
		work(x,n-1,c1,c2);
		c1[n]=min(c1[n-1],c2[n-1]+2);
		c2[n]=min(c1[n-1],c2[n-1])+1+g[n-2];
    }
//递归求解x在子图d[n-1]中的情况,编号仍为x
//(因为子图d[n-1]和d[n-2]构成d[n]时,d[n-1]中,点的编号都没有变)

//先考虑x到起点的距离:
//因为d[n-1]和d[n-2]构成d[n]时,新增了两条长度为1的边,
//分别是起点1到割点|d[n-1]|+1 和 图d[n-1]的终点|d[n-1]|到割点|d[n-1]|+1
//所以子图d[n-1]中,起点1到终点|d[n-1]|之间新增了一条长度为2的边,所以x到起点的路径多了一种可能
//即x先到终点|d[n-1]|再到起点1,距离为c2[n-1]+2;
//与原来的最短距离c1[n-1]取min就是当前最短距离

//再考虑x到终点的距离:
//因为图d[n]的终点在子图d[n-2]中,而x在子图d[n-1]中,
//还是因为新增了两条边,所以现在x到终点有两条路径
//第一条:x先到 起点1 再到割点|d[n-1]|+1 最后到终点,距离为c1[n-1]+1+g[n-2]
//第二条:x先到 子图d[n-1]的终点|d[n-1]| 再到割点|d[n-1]|+1 最后到终点,距离为c2[n-1]+1+g[n-2]
//(g[n-2]我们之前已经预处理出了,它记录的是图d[n-2]中 起点到终点的最短距离)
//(此时(图d[n-1]和d[n-2]构成d[n]之后),
//图d[n-2]的起点就是图d[n]的割点|d[n-1]|+1,图d[n-2]的终点就是图d[n]的终点)
    else{//如果x在d[n]的子图d[n-2]中
		work(x-d[n-1],n-2,c1,c2);
		c1[n]=c1[n-2]+1;
		c2[n]=c2[n-2];
    }
//递归求解x在子图d[n-2]中的情况,编号变为x-|d[n-1]|
//(因为d[n-1]和d[n-2]构成d[n]时,子图d[n-2]中,点的编号都加上了|d[n-1]|)

//先考虑x到起点的距离:
//因为在图d[n]中,x到起点1的路径只有一条,即x先到 割点|d[n-1]|+1 再到起点1
//割点|d[n-1]|+1 到起点1之间有一条新增边,所以最短距离就是1
//x到 割点|d[n-1]|+1 的最短距离为什么是c1[n-2]呢?
//c1[n-2]记录的是图d[n-2]中,x到起点的最短距离;而图d[n-2]的起点就是图d[n]的割点.

//再考虑x到终点的距离:
//因为图d[n]的终点就是图d[n-2]的终点,所以就是c2[n]=c2[n-2]
}
LL dis(LL u,LL v,int n) {
    if(n<=1)return u!=v;
//边界情况:
//图d[0]中只有一个点1,u必然等于v,最短距离为0
//图d[1]中只有两个点1和2,如果u!=v,即一个是点1,一个是点2,则最短距离为1,否则就是0了
    
//如果对于下面三种情况的最短距离的计算方法不理解,请结合上面的两幅图 再认真理解一遍work函数的注释
    if(u<=d[n-1]){
	if(v>d[n-1])return min(a1[n-1],a2[n-1])+1+b1[n-2];
//上述第一种情况:u在子图d[n-1]中,v在子图d[n-2]中,两条路径
//路径1:u先到 起点1 再到 割点|d[n-1]|+1 最后到v,距离为a1[n-1]+1+b1[n-2]
//路径2:u先到 图d[n-1]的终点 再到割点|d[n-1]|+1 最后到v,距离为a2[n-1]+1+b1[n-2]
	else return min(dis(u,v,n-1),min(a1[n-1]+b2[n-1],a2[n-1]+b1[n-1])+2);
//上述第三种情况:u,v都在子图d[n-1]中,两条路径
//路径1:u先到 起点1 再到割点 再到图d[n-1]的终点 最后到v,距离为a1[n-1]+1+1+b2[n-1]
//路径2:u先到 图d[n-1]的终点 再到割点 再到起点 最后到v,距离为a2[n-1]+1+1+b1[n-1]
//因为u,v在同一个子图中,所以它们还可以分解为更小的子问题即dis(u,v,n-1)
    }
    else return dis(u-d[n-1],v-d[n-1],n-2);
//上述第二种情况:u,v都在子图d[n-2]中
//两个点的编号都减去|d[n-1]|,回到图d[n-2]中求解子问题(为什么要减?请认真看work函数的注释)
}
int main(){
    scanf("%d %d",&m,&n);
    n=min(n,80);
    d[0]=1;d[1]=2;
    for(int i=2;i<=n;i++)
		d[i]=d[i-1]+d[i-2];
    g[0]=0;g[1]=g[2]=1;//g[i]表示 在图d[i]中起点到终点的最短距离
    for(int i=3;i<=n;i++)
		g[i]=g[i-2]+1;//根据构图方式可得出的规律
    while(m--){
		LL u,v;
		scanf("%lld %lld",&u,&v);
		if(u>v)swap(u,v);//保证点u的编号小于点v的编号,方便分类讨论.
		work(u,n,a1,a2);//预处理 在图d[n]中u分别到 起点和终点的距离a1[n]和a2[n]
		work(v,n,b1,b2);//预处理 在图d[n]中v分别到 起点和终点的距离b1[n]和b2[n]
		printf("%lld
",dis(u,v,n));
    }
    return 0;
}

P.S.写这篇博客花了两三个小时...