题意:设(T=(V,E,W))是一个无圈且连通的无向图(也称为无根树),每条边到有正整数的权,我们称(T)为树网(treebetwork),其中(V),(E)分别表示结点与边的集合,(W)表示各边长度的集合,并设(T)有(n)个结点。
路径:树网中任何两结点(a),(b)都存在唯一的一条简单路径,用(d(a, b))表示以(a, b)为端点的路径的长度,它是该路径上各边长度之和。我们称(d(a, b))为(a, b)两结点间的距离。
(D(v, P)=min{d(v, u)}), (u)为路径(P)上的结点。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网(T),直径不一定是唯一的,但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距(mathrm{ECC}(F)):树网T中距路径F最远的结点到路径(F)的距离,即
(mathrm{ECC}(F)=max{d(v, F),v in V})
任务:对于给定的树网(T=(V, E, W))和非负整数(s),求一个路径(F),他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过(s)(可以等于s),使偏心距(ECC(F))最小。我们称这个路径为树网(T=(V, E, W))的核(Core)。必要时,(F)可以退化为某个结点。一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
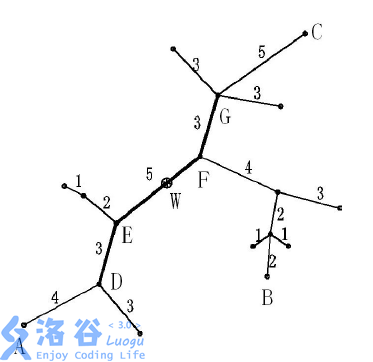
下面的图给出了树网的一个实例。图中,(A-B)与(A-C)是两条直径,长度均为(20)。点(W)是树网的中心,(EF)边的长度为(5)。如果指定(s=11),则树网的核为路径DEFG(也可以取为路径DEF),偏心距为(8)。如果指定(s=0)(或(s=1)、(s=2)),则树网的核为结点(F),偏心距为(12)。
题面真长,但实际上基本都是我们已经知道了的概念.
分析:这道题(NOIP)原题数据是(n<=300),可以考虑(n^3,n^2)来做.我们两次(DFS)求出一条直径,并记录路径,在直径上每次枚举两个距离不超过s的点(p,q),(p,q)之间的路径作为"树网的核",然后把(p,q)之间的每个点都"标记",接下来,从"树网的核"上的每个节点出发,(DFS),不经过被"标记"的节点,求出""### 这道题(NOIP)原题数据是(n<=300),可以考虑(n^3,n^2)来做.我们两次(DFS)求出一条直径,并记录路径,在直径上每次枚举两个距离不超过s的点(p,q),(p,q)之间的路径作为"树网的核",然后把(p,q)之间的每个点都"标记",接下来,从"树网的核"上的每个节点出发,(DFS),不经过被"标记"的节点,求出"树网的核"以外的每个节点到"树网的核"的距离,最大值就是"核的偏心距",在所有"核的偏心距"中取最小值就是答案.这是(n^3)做法.
实际上,我们贪心一下,每次枚举"树网的核"的一个端点,另一个端点在距离不超过s的前提下,显然越远越好,所以我们可以直接确定另一个端点,这样时间复杂度就是(n^2)的了.
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define ll long long
using namespace std;
inline int read(){
int x=0,o=1;char ch=getchar();
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')o=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*o;
}
const int N=305;
int n,s,sum,ans=1e9;
int dis[N],pre[N],zz[N],bj[N],dist[N];
int tot,head[N],nxt[N<<1],to[N<<1],w[N<<1];
inline void add(int a,int b,int c){
nxt[++tot]=head[a];head[a]=tot;
to[tot]=b;w[tot]=c;
}
inline void dfs1(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa)continue;
dis[v]=dis[u]+w[i];dfs1(v,u);
}
}
inline void dfs2(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa)continue;
dis[v]=dis[u]+w[i];pre[v]=u;dfs2(v,u);
}
}
inline void dfs3(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa||bj[v])continue;
dist[v]=dist[u]+w[i];dfs3(v,u);
}
}
int main(){
n=read();s=read();
for(int i=1;i<n;++i){
int a=read(),b=read(),c=read();
add(a,b,c);add(b,a,c);
}
dfs1(1,0);int pos1,pos2,maxn=0;
for(int i=1;i<=n;++i)if(dis[i]>maxn)maxn=dis[i],pos1=i;
memset(dis,0,sizeof(dis));dfs2(pos1,0);
maxn=0;for(int i=1;i<=n;++i)if(dis[i]>maxn)maxn=dis[i],pos2=i;
while(pos2!=pos1){zz[++sum]=pos2;pos2=pre[pos2];}zz[++sum]=pos1;
reverse(zz+1,zz+sum+1);
for(int l=1;l<=sum;++l){//枚举左端点
int r;
for(int i=l;i<=sum;++i){
if(dis[zz[i]]-dis[zz[l]]<=s)r=i;//找到最远的右端点
else break;
}
for(int i=1;i<=n;++i)bj[i]=0,dist[i]=0;//初始化
for(int k=l;k<=r;++k)bj[zz[k]]=1;//标记"树网的核"上的点
for(int k=l;k<=r;++k)dfs3(zz[k],0);//从"树网的核"上的每个节点开始dfs
maxn=0;for(int i=1;i<=n;++i)maxn=max(maxn,dist[i]);//找到偏心距
ans=min(ans,maxn);//更新最小偏心距
}
printf("%d
",ans);
return 0;
}
我们要想办法优化到(O(n)).设直径上的节点为(zz_1,zz_2,...,zz_{sum}),(dist[i])表示从(zz_i)出发,不经过直径上其它节点,能够到达的最远的距离.以(zz_i,zz_j(i<=j))为端点的树网的核的偏心距就是(max(max_{1<=k<=sum}dist[zz_k],dis(zz_1,zz_i),dis(zz_j,zz_t))).显然(max_{1<=k<=sum}dist[zz_k])是个定值,(dis(zz_1,zz_i),dis(zz_j,zz_t))可以借助第二次dfs时的(dis)数组(O(1))计算.
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#define ll long long
using namespace std;
inline int read(){
int x=0,o=1;char ch=getchar();
while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
if(ch=='-')o=-1,ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return x*o;
}
const int N=5e5+5;
int n,s,sum,ans=1e9;
int dis[N],pre[N],zz[N],bj[N],dist[N];
int tot,head[N],nxt[N<<1],to[N<<1],w[N<<1];
inline void add(int a,int b,int c){
nxt[++tot]=head[a];head[a]=tot;
to[tot]=b;w[tot]=c;
}
inline void dfs1(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa)continue;
dis[v]=dis[u]+w[i];dfs1(v,u);
}
}
inline void dfs2(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa)continue;
dis[v]=dis[u]+w[i];pre[v]=u;dfs2(v,u);
}
}
inline void dfs3(int u,int fa){
for(int i=head[u];i;i=nxt[i]){
int v=to[i];if(v==fa||bj[v])continue;
dist[v]=dist[u]+w[i];dfs3(v,u);
}
}
int main(){
n=read();s=read();
for(int i=1;i<n;++i){
int a=read(),b=read(),c=read();
add(a,b,c);add(b,a,c);
}
dfs1(1,0);int pos1,pos2,maxn=0;
for(int i=1;i<=n;++i)if(dis[i]>maxn)maxn=dis[i],pos1=i;
memset(dis,0,sizeof(dis));dfs2(pos1,0);
maxn=0;for(int i=1;i<=n;++i)if(dis[i]>maxn)maxn=dis[i],pos2=i;
while(pos2!=pos1){zz[++sum]=pos2;bj[pos2]=1;pos2=pre[pos2];}
zz[++sum]=pos1;bj[pos1]=1;reverse(zz+1,zz+sum+1);
for(int i=1;i<=sum;++i)dfs3(zz[i],0);
maxn=0;for(int i=1;i<=n;++i)maxn=max(maxn,dist[i]);//找到最大的dist,即得到上面那个定值
for(int i=1,j=1;i<=sum;++i){//枚举"树网的核"的一个端点i
while(dis[zz[j]]-dis[zz[i]]<=s&&j<=sum){//不断扩展到最远的另一个端点j
ans=min(ans,max(maxn,max(dis[zz[i]]-dis[zz[1]],dis[zz[sum]]-dis[zz[j]])));//每次考虑更新答案.
++j;
}
}
printf("%d
",ans);
return 0;
}
