<更新提示>
<第一次更新>
阅读本文前,请确保已经阅读并理解了如下两篇文章:
『线段树 Segment Tree』
『线段树简单运用』
<正文>
引入
这是一种由(THU-zkw)大佬发明的数据结构,本质上是经典的线段树区间划分思想,采用了自底向上的方式传递区间信息,避免的递归结构,其代码相对经典线段树更简单,常数更小,易于实现。
统计的力量-源自这里。
基础非递归
接下来,我们将讲解(zkw)线段树的第一种实现形式,用于单点修改 区间查询,我们以查询区间最大值为例来讲解。
建树
普通线段树需要建树,(zkw)线段树当然也需要建树。
考虑线段树的一个性质,其树上的叶节点代表的往往都是形如([x,x])的元区间,而且除最后一层外,线段树是一颗满二叉树,所以我们要把这颗线段树的数组大小先申请好了。
一棵满二叉树有(x)个节点时,它有(frac{x+1}{2})个叶子节点,而我们需要至少(n)个叶子节点的线段树,即使(frac{x+1}{2}geq n),那么我们设(x=1),在(frac{x+1}{2}<n)时不断执行(x*=2),就能得到足够大小的线段树下标(base),由于线段树的叶子节点可能分布在两层,所以保险起见,我们还需再将(x)扩大一倍,即在(x+1<n)时不断执行(x*=2)就可以了。
得到合适的下标位置后,将(1-n)下标位置的原数据直接存入线段树的叶子节点即可。
其实,我们还需将下标再扩大两个位置,即需要保证(x>n),才停止执行(x*=2)。其原因是这样的:在执行区间查询操作时,我们需要将查询区间([l,r])更改为((l,r))(关于原因,我们之后再分析),才便于(zkw)线段树的查询,那么在询问([1,n])时,可能为调用到([0,n+1])的原下标,所以还需再扩大两个位置。
得到了合适的下标(base)并将(1-n)的数据存入对应位置后,当然我们还要对(1)到(base-1)的线段树位置进行区间更新,这个普通的更新就可以了。
(Code:)
inline void reset(void)
{
memset( val , 0 , sizeof val );
base = 1;
}
inline void build(int *s,int len)
{
for (;base<=len;base<<=1);
for (int i=base+1;i<=base+len;i++)
val[i] = s[i-base];
for (int i=base-1;i>=1;i--)
val[i] = max( val[i<<1] , val[i<<1|1] );
}
单点修改
直接在叶节点上修改对应的值,然后更新其每一个父节点即可。
(Code:)
inline void modify(int pos,int x)
{
pos += base;val[pos] = x;
for (pos>>=1;pos;pos>>=1)
val[pos] = max( val[pos<<1] , val[pos<<1|1] );
}
区间查询
我们先来看一个最大值线段树。
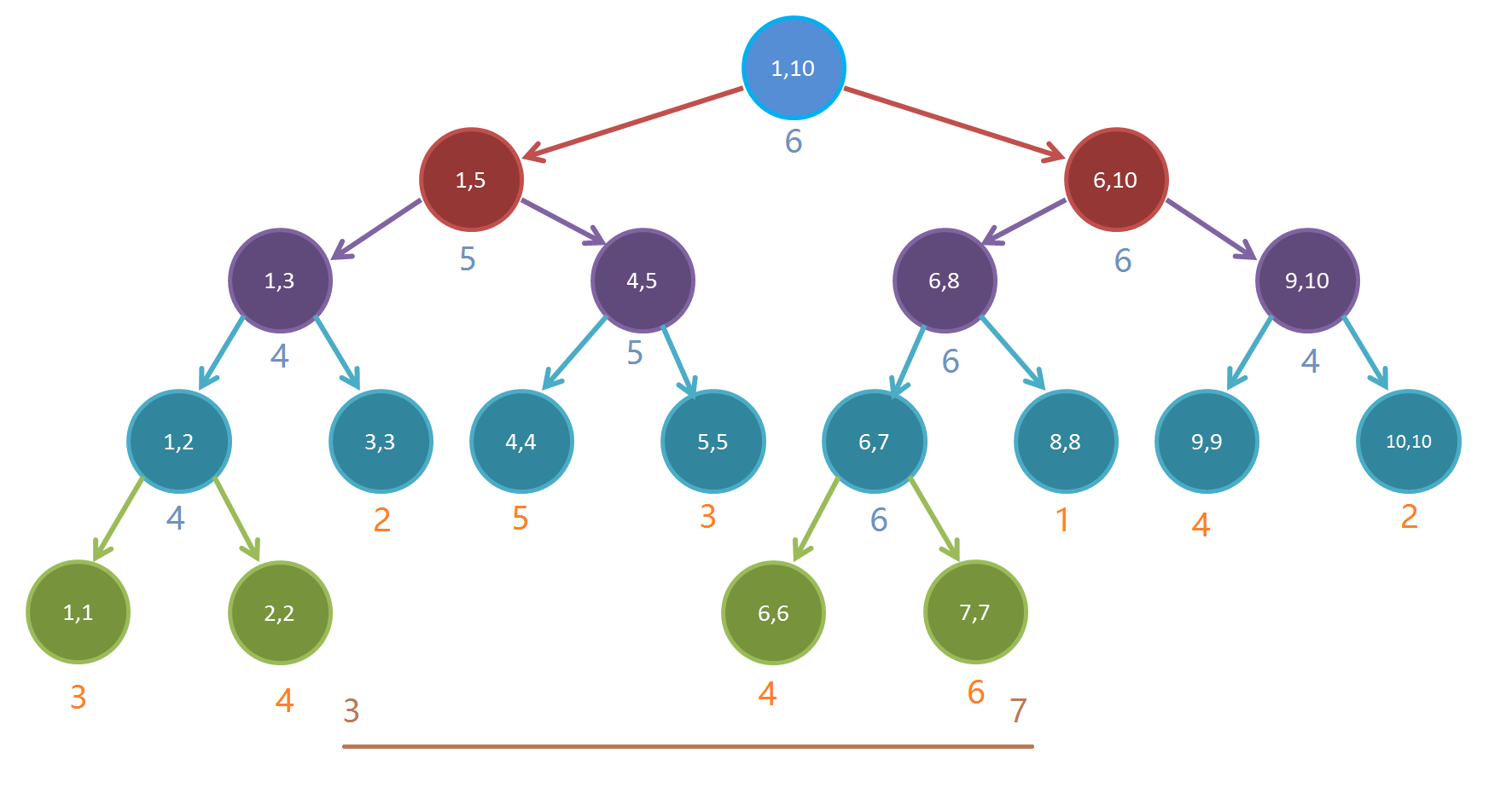
其中,叶节点下面的橙色代表数组上的原数值,淡蓝色代表线段树对应节点的区间最大值,棕色代表查询区间的范围,如图,我们需要查询区间([3,7])的最大值。
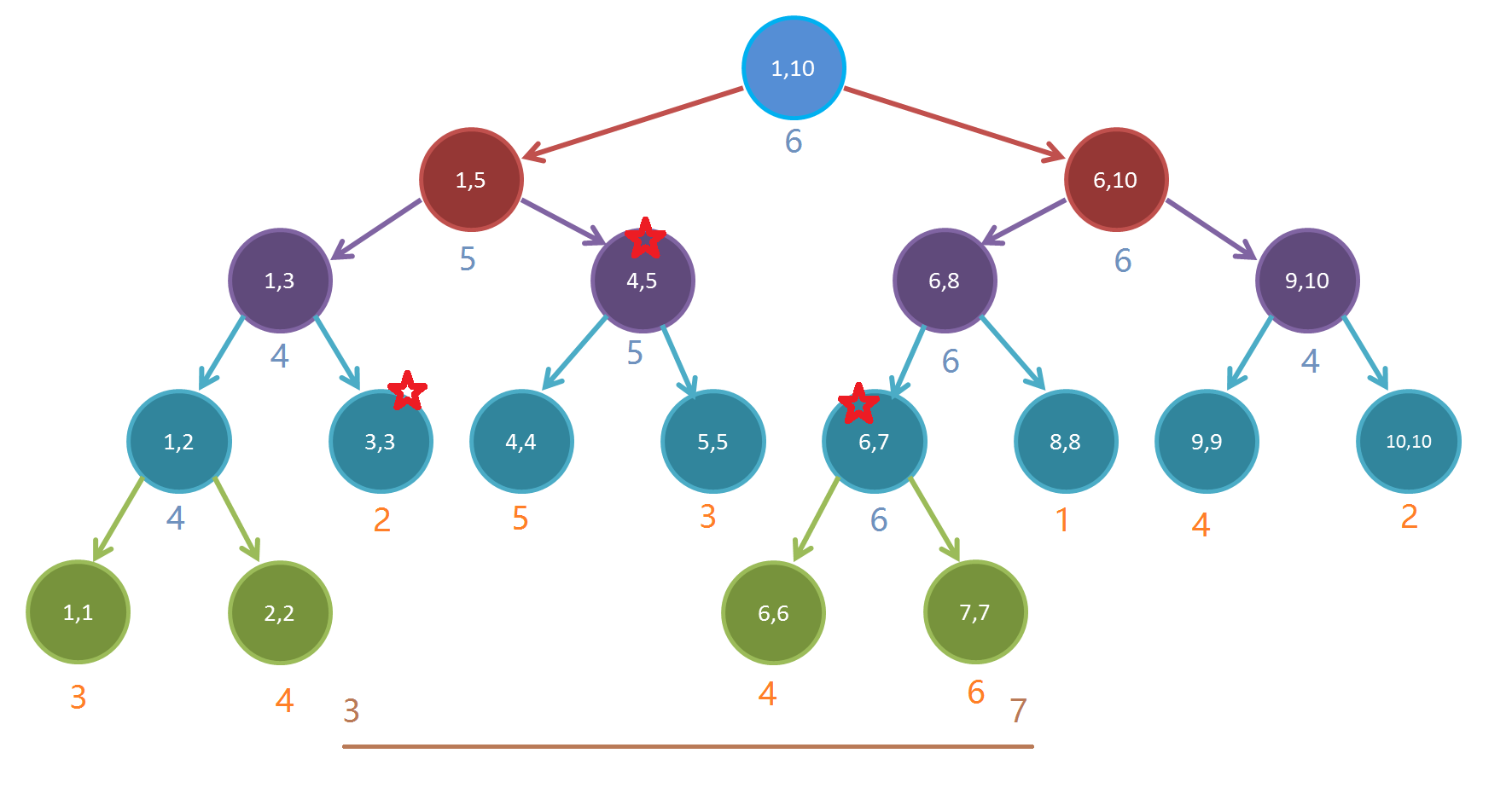
显然,我们只要查询上图带五角星的几个线段树节点的关键值,就能得知最大值。
在(zkw)线段树上,我们考虑如下一种方式:
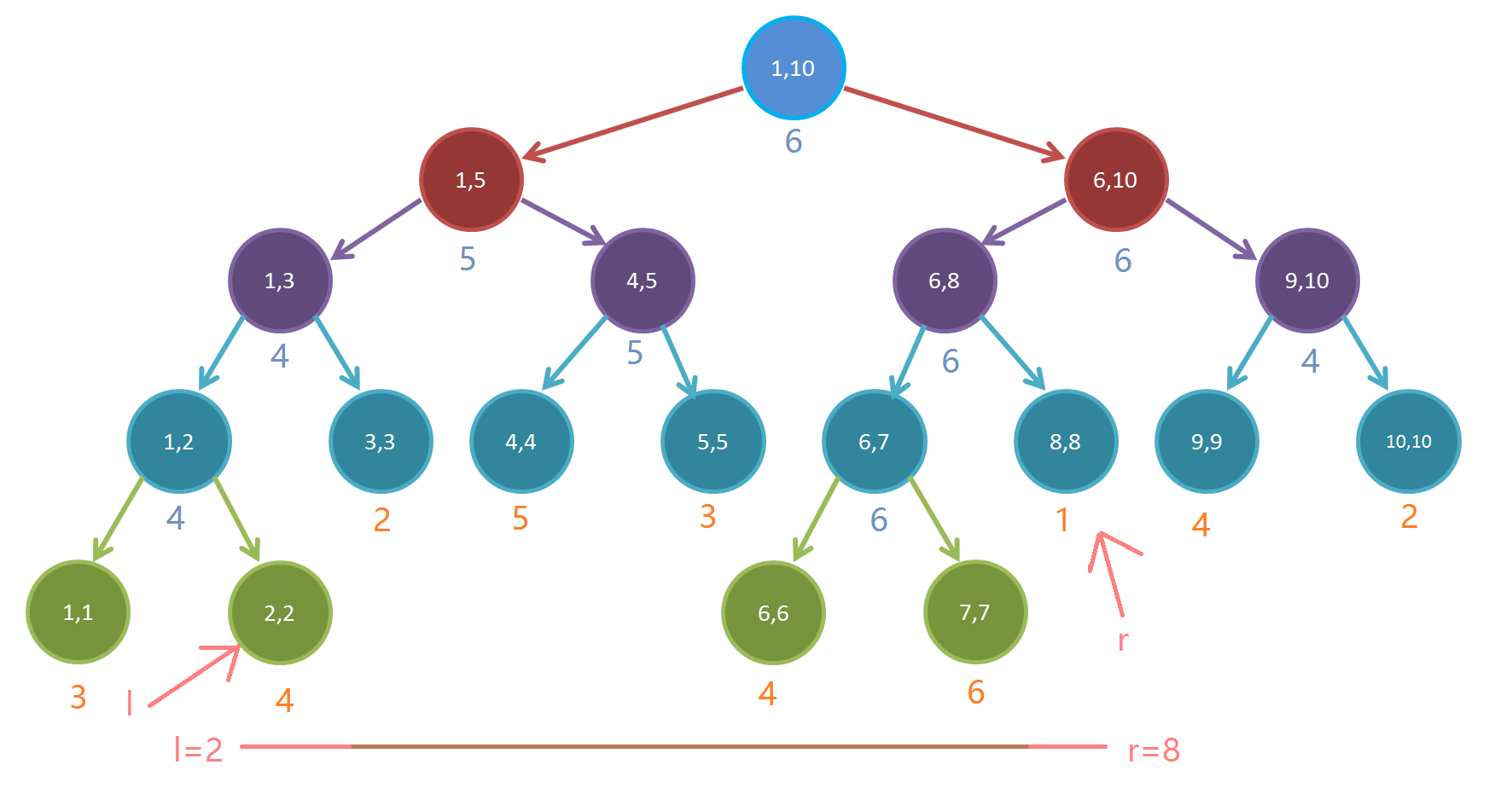
先将闭区间([3,7])拓展为开区间((2,8)),我们设两个指针(l=2,r=8)。
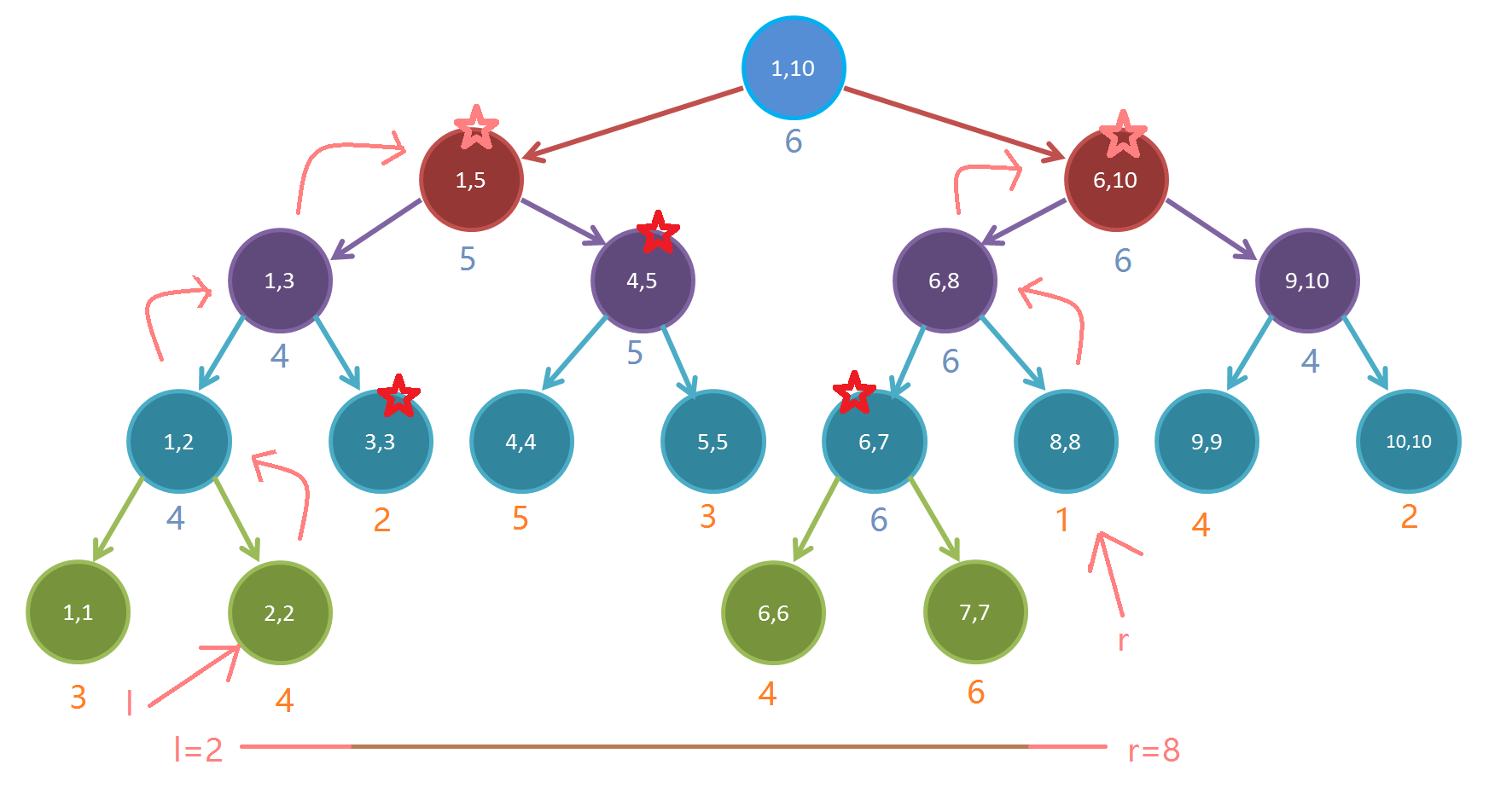
然后让(l,r)依次向上找父亲节点,直到两个节点(l,r)的父亲节点相同,我们停止向上查找。此时,结束位置的两个节点标记了粉色星,需要查询的节点还是标记的红色星。
不难发现规律:当指针(l)经过的节点是一个左儿子时,或者当指针(r)经过的节点是一个右儿子时,它的兄弟就是一个需要查询的节点。
对于一个查询,我们只需将闭区间转换为开区间,就能通过向上找父亲的遍历得到区间的答案,这就是使用开区间,并要求数组大小至少大于原大小两个位置的原因。
(Code:)
inline int query(int l,int r)
{
int res = 0;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
if ( ~ l & 1 )res = max( res , val[l^1] );
if ( r & 1 )res = max( res , val[r^1] );
}
return res;
}
至此,我们就能用极短的代码和很高的效率实现单点修改,区间查询的线段树了。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N=100200;
int val[N<<2],base,n,a[N];
inline void read(int &k)
{
int x=0,w=0;char ch;
while (!isdigit(ch))
w |= ch=='-' , ch=getchar();
while (isdigit(ch))
x = x*10 + ch-48 , ch=getchar();
k=(w?-x:x);return;
}
inline void reset(void)
{
memset( val , 0 , sizeof val );
base = 1;
}
inline void build(int *s,int len)
{
for (;base<=len;base<<=1);
for (int i=base+1;i<=base+len;i++)
val[i] = s[i-base];
for (int i=base-1;i>=1;i--)
val[i] = max( val[i<<1] , val[i<<1|1] );
}
inline void modify(int pos,int x)
{
pos += base;val[pos] = x;
for (pos>>=1;pos;pos>>=1)
val[pos] = max( val[pos<<1] , val[pos<<1|1] );
}
inline int query(int l,int r)
{
int res = 0;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
if ( ~ l & 1 )res = max( res , val[l^1] );
if ( r & 1 )res = max( res , val[r^1] );
}
return res;
}
int main(void)
{
read(n);
reset();
build(a,n);
for (int i=1;i<=n;i++)
{
int op,k1,k2;
read(op);read(k1);read(k2);
if (op==1)modify(k1,k2);
if (op==2)printf("%d
",query(k1,k2));
}
return 0;
}
简单标记
在此,我们要实现(zkw)线段树的第二种基本形式,用于区间修改 区间求和。
标记永久化
对于区间修改 区间求和的(zkw)线段树,最重要的思想就是标记永久化的思想。
对于区间修改,我们在普通线段树上是通过(lazytag)的标记方式实现的,对于修改和查询操作调用到时,再下传标记。而在(zkw)线段树中,显然向下传递标记的方式是毫无用武之地了。那么,我们引入一种新的标记思想:标记永久化。
对于一个节点,若修改操作对节点所代表的整个区间产生影响,显然我们可以直接对该节点进行标记,而非逐层递归修改。那么,在自底向上的线段树中,我们可以不下传标记,而是在每一次查询时,统计累加一路上所有标记对答案产生的影响,这种标记思想被称为标记永久化。
建树
该版本(zkw)线段树的建树方式和第一种形式的(zkw)线段树的建树方式一致,不再重复说明。
(Code:)
inline void build(void)
{
for (;base<=n;base<<=1);
for (int i=base+1;i<=base+n;i++)
val[i] = a[i-base];
for (int i=base-1;i>=1;i--)
val[i] = val[i<<1] + val[i<<1|1] ;
}
区间修改
关于标记永久化,我们进行定义:(add_i)代表线段树中(i)号节点的关键值已经进行修改,但是其所有子节点均有一个值为(add_i)的增量未进行处理。
我们采用上一版本(zkw)线段树区间查询的方式,设置两个开区间指针(l,r),并同时向上遍历。同时,我们维护三个变量(lcnt,rcnt,cnt),分别代表左指针处理增量的节点个数,右指针处理增量的节点个数,两个指针当前所在节点左包含的叶节点个数。
然后利用上述变量和(add)标记的定义,沿路更新(add)标记和原线段树即可,当然,对于(l,r)成为兄弟后,我们还须将(add)标记一直上推到根节点。
(Code:)
inline void modify(int l,int r,long long delta)
{
long long lcnt = 0 , rcnt = 0 , cnt = 1 ;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 , cnt<<=1 )
{
val[l] += delta*lcnt;
val[r] += delta*rcnt;
if ( ~ l & 1 )
add[l^1] += delta , val[l^1] += delta*cnt , lcnt += cnt;
if ( r & 1 )
add[r^1] += delta , val[r^1] += delta*cnt , rcnt += cnt;
}
for (; l || r ; l>>=1 , r>>=1 )
val[l] += delta*lcnt , val[r] += delta*rcnt;
}
区间求和
有了(add)标记,我们就很容易求得区间的和了。还是一样的方式,将闭区间转换为开区间,然后向上遍历,同样维护(lcnt,rcnt,cnt),然后利用(add)标记进行累加,再加上原来的区间和,就能得到答案。
(Code:)
inline long long query(int l,int r)
{
long long lcnt = 0 , rcnt = 0 , cnt = 1 ;
long long res = 0;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 , cnt<<=1 )
{
if (add[l]) res += add[l]*lcnt;
if (add[r]) res += add[r]*rcnt;
if ( ~ l & 1 )
res += val[l^1] , lcnt += cnt;
if ( r & 1 )
res += val[r^1] , rcnt += cnt;
}
for (; l || r ; l>>=1 , r>>=1 )
res += add[l]*lcnt , res += add[r]*rcnt;
return res;
}
至此,我们已经实现了支持区间修改,区间求和的(zkw)线段树了,对于更多需要维护求和性质的值,也可以使用标记永久化的思想,这需要读者理解掌握。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N=100020;
long long n,q,a[N],val[N<<2],base,add[N<<2];
inline void reset(void)
{
memset( val , 0 , sizeof val );
memset( add , 0 , sizeof add );
base = 1;
}
inline void build(void)
{
for (;base<=n;base<<=1);
for (int i=base+1;i<=base+n;i++)
val[i] = a[i-base];
for (int i=base-1;i>=1;i--)
val[i] = val[i<<1] + val[i<<1|1] ;
}
inline void modify(int l,int r,long long delta)
{
long long lcnt = 0 , rcnt = 0 , cnt = 1 ;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 , cnt<<=1 )
{
val[l] += delta*lcnt;
val[r] += delta*rcnt;
if ( ~ l & 1 )
add[l^1] += delta , val[l^1] += delta*cnt , lcnt += cnt;
if ( r & 1 )
add[r^1] += delta , val[r^1] += delta*cnt , rcnt += cnt;
}
for (; l || r ; l>>=1 , r>>=1 )
val[l] += delta*lcnt , val[r] += delta*rcnt;
}
inline long long query(int l,int r)
{
long long lcnt = 0 , rcnt = 0 , cnt = 1 ;
long long res = 0;
for ( l=base+l-1 , r=base+r+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 , cnt<<=1 )
{
if (add[l]) res += add[l]*lcnt;
if (add[r]) res += add[r]*rcnt;
if ( ~ l & 1 )
res += val[l^1] , lcnt += cnt;
if ( r & 1 )
res += val[r^1] , rcnt += cnt;
}
for (; l || r ; l>>=1 , r>>=1 )
res += add[l]*lcnt , res += add[r]*rcnt;
return res;
}
inline void solve(void)
{
scanf("%lld%lld",&n,&q);
for (int i=1;i<=n;i++)
scanf("%lld",&a[i]);
reset();
build();
for (int i=1;i<=q;i++)
{
char op;
scanf("
%c",&op);
if (op=='C')
{
int l,r;long long delta;
scanf("%d%d%lld",&l,&r,&delta);
modify(l,r,delta);
}
if (op=='Q')
{
int l,r;
scanf("%d%d",&l,&r);
printf("%lld
",query(l,r));
}
}
}
int main(void)
{
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
solve();
return 0;
}
差分思想和区间最值
接下来,我们将要尝试实现使用区间查询的另一种形式,区间最值的查询。
用上述两个模板稍微结合,更改一下难道不就可以实现区间修改,区间最值的(zkw)线段树了吗?答案是否定的。在区间修改的限制下,如果还用标记永久化的思想,由于标记的大小和位置未知,那么区间最值的查询就会出问题。
差分思想
现在,我们线段树上的节点将不再存对应区间的关键值了。我们需要用(zkw)线段树来维护原关键值的差分值,若原来的(val_i)代表节点(i)所代表区间的最大值,则现在我们需要维护的(val'_i=val_i-val_{i/2}),特殊地,(val_1)仍代表整个区间的最大值。
可能读者已经发现一点性质了:从任意叶节点(y)开始,一直向上找父亲,并累加对应点的权值,就得到了原节点的权值。
其实,我们还可以用这样的方式理解:(val_i)代表(i)节点所在区间的最大值比其父亲节点所在区间最大值大多少(可能负数)。
建树
还是可以利用和之前一样的方式建树,特殊地,在存完一个节点的值以后要利用(val_i)的定义来计算得到差分的值。
(Code:)
inline void build(void)
{
for (;base<=n;base<<=1);
for (int i=base+1;i<=base+n;i++)
val[i] = a[i-base];
for (int i=base;i>=1;i--)
val[i] = max( val[i<<1] , val[i<<1|1] ) ,
val[i<<1] -= val[i] , val[i<<1|1] -= val[i];
}
区间修改
有了差分线段树以后,我们发现区间修改就可以直接在树上操作了。还是利用开区间的方式,向上查找父亲并更新线段树,对于沿路访问到的每一个节点,由于可能其子树中包含修改过的节点,就要利用差分定义上传一下差值给父亲,就还能维护之前所提到的性质,而不用再去操作子节点。
同样地,对于(l,r)指针成为兄弟后,还需将差值上推到根节点。
(Code:)
inline void modify(int l,int r,int delta)
{
int temp;
for ( l=l+base-1 , r=r+base+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
if ( ~ l & 1 ) val[l^1] += delta;
if ( r & 1 ) val[r^1] += delta;
temp = max( val[l] , val[l^1] );
val[l] -= temp , val[l^1] -= temp , val[l>>1] += temp;
temp = max( val[r] , val[r^1] );
val[r] -= temp , val[r^1] -= temp , val[r>>1] += temp;
}
for (; l > 1 ; l>>=1 )
temp = max( val[l] , val[l^1] ) ,
val[l] -= temp , val[l^1] -= temp , val[l>>1] += temp;
}
区间最值
维护了这样一颗差分线段树,我们就可以用一种简单的方式来查询区间最值了。
这次,我们维护(l,r)为闭区间的左右指针,在向上找父亲遍历的过程中,对左右指针遍历到节点的区间差分值取一下最大值,再一直向上累加,累加到根节点,就是区间最大值,这和单点向上累加的道理是一样的。
(Code:)
inline int query(int l,int r)
{
int lres = 0 ,rres = 0;
l += base , r += base;
if ( l ^ r )
{
for (; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
lres += val[l] , rres += val[r];
if ( ~ l & 1 ) lres = max( lres , val[l^1] );
if ( r & 1 ) rres = max( rres , val[r^1] );
}
}
int res = max( lres + val[l] , rres + val[r] );
while ( l > 1 ) res += val[l>>=1];
return res;
}
这样,(zkw)线段树的三类基础模板就已经得到实现了,有关更多的拓展,需要我们灵活运用。
(Code:)
#include <bits/stdc++.h>
using namespace std;
const int N=100200;
int val[N<<2],n,a[N],base;
inline void read(int &k)
{
int x=0,w=0;char ch;
while (!isdigit(ch))
w |= ch=='-' , ch=getchar();
while (isdigit(ch))
x = x*10 + ch-48 , ch=getchar();
k=(w?-x:x);return;
}
inline void reset(void)
{
memset( val , 0 , sizeof val );
base = 1;
}
inline void build(void)
{
for (;base<=n;base<<=1);
for (int i=base+1;i<=base+n;i++)
val[i] = a[i-base];
for (int i=base;i>=1;i--)
val[i] = max( val[i<<1] , val[i<<1|1] ) ,
val[i<<1] -= val[i] , val[i<<1|1] -= val[i];
}
inline void modify(int l,int r,int delta)
{
int temp;
for ( l=l+base-1 , r=r+base+1 ; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
if ( ~ l & 1 ) val[l^1] += delta;
if ( r & 1 ) val[r^1] += delta;
temp = max( val[l] , val[l^1] );
val[l] -= temp , val[l^1] -= temp , val[l>>1] += temp;
temp = max( val[r] , val[r^1] );
val[r] -= temp , val[r^1] -= temp , val[r>>1] += temp;
}
for (; l > 1 ; l>>=1 )
temp = max( val[l] , val[l^1] ) ,
val[l] -= temp , val[l^1] -= temp , val[l>>1] += temp;
}
inline int query(int l,int r)
{
int lres = 0 ,rres = 0;
l += base , r += base;
if ( l ^ r )
{
for (; l ^ r ^ 1 ; l>>=1 , r>>=1 )
{
lres += val[l] , rres += val[r];
if ( ~ l & 1 ) lres = max( lres , val[l^1] );
if ( r & 1 ) rres = max( rres , val[r^1] );
}
}
int res = max( lres + val[l] , rres + val[r] );
while ( l > 1 ) res += val[l>>=1];
return res;
}
inline void solve(void)
{
scanf("%d",&n);
reset();
build();
for (int i=1;i<=n;i++)
{
int op,k1,k2;
read(op),read(k1),read(k2);
if (op==1)modify(k1,k2,1);
if (op==2)printf("%d
",query(k1,k2));
}
}
int main(void)
{
solve();
return 0;
}
<后记>