【动态规划】动态$DP$ (树链剖分维护&&LCT维护)
一、不带修改的树形$DP$
有这样一道题:没有上司的舞会
我们可以很快地得出树形$DP$的转移方程,以达到$O(N)$求解
void dfs (int u,int fa) { for (int i=head[u];i!=0;i=e[i].nxt) if (e[i].v!=fa) { dfs (e[i].v,u); f[u][0]+=max (f[e[i].v][0],f[e[i].v][1]); f[u][1]+=f[e[i].v][0]; } f[u][1]+=p[u]; }
二、带修改的树形DP与矩阵乘法,树链剖分的联系
但如果带上修改呢?如这道题:动态DP
我们不可能每修改一次便$O(N)$ $DP$一次
但我们会发现一次修改会导致树上从该点到根结点的路径改变,既然是树上路径的修改与查询,我们自然会想起树链剖分——处理树上路径问题的利器
考虑这样一个状态转移方程我们可以用矩阵乘法来表示出来:
$C_{i}^{j} = max_{k = 1}^{n} A_{i}^{k} + B_{k}^{j} $
这个矩阵乘法与之前的并不一样,但依然满足乘法交换律
于是我们可以在树链剖分后用线段树维护矩阵的乘积
三、构造矩阵
我们从不带修改的树形$DP$研究,设:
$f [u][0]$:表示子树$u$中不选$u$的最大权独立集大小
$f [u][1]$:表示子树$u$中选$u$的最大权独立集大小。
在树链剖分后形成了若干轻链与重链,如下图:
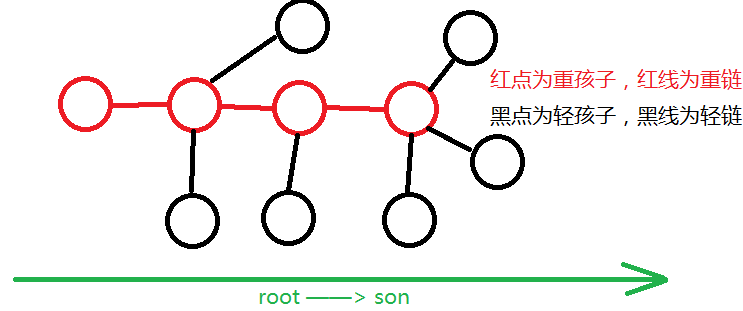
右边的孩子深度较大
如图的所有黑点(所有$top$的深度比这条重链深的重链的 $top$)的$f [v]$,$g[v]$ 已经求出来了;
我们考虑怎么转移:设一个重孩子为$u$,它所有轻孩子为$v$,它右边的重孩子为$u+1$;
设$g[u][0]$表示不选u时,$u$所有轻孩子的最大权独立集大小,g[u][1]表示选$u$时,$u$所有轻孩子再加上$u$自己的最大权独立集大小。
则:$f [u][0]=g[u][0]+max (f [u+1][0],f [u+1][1])$
$f [u][1]=g[u][1]+f [u+1][0]$
我们就可以构造出这样的一个矩阵乘法DP转移
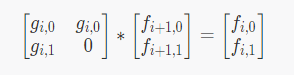
我们在树上每个结点维护第一个2*2的矩阵
用树剖+线段树维护区间矩阵乘积即可
时间复杂度:$O(Nlog^2 N)$
空间复杂度:$O (N)$
代码如下:
1 #include<bits/stdc++.h> 2 #define MAXN 100010 3 using namespace std; 4 inline int read () 5 { 6 int w=1,s=0; 7 char ch=getchar (); 8 while (ch<'0'||ch>'9'){if (ch=='-') w=-1;ch=getchar ();} 9 while ('0'<=ch&&ch<='9') s=(s<<1)+(s<<3)+(ch^48),ch=getchar (); 10 return s*w; 11 } 12 struct Matrix{ 13 int a[3][3]; 14 Matrix (){memset (a,0,sizeof (a));} 15 Matrix operator * (const Matrix &rhs) const 16 { 17 Matrix c; 18 for (int i=1;i<=2;i++) 19 for (int j=1;j<=2;j++) 20 for (int k=1;k<=2;k++) 21 c.a[i][j]=max (c.a[i][j],a[i][k]+rhs.a[k][j]); 22 return c; 23 } 24 }val[MAXN]; 25 struct SEG{ 26 int l,r;Matrix v; 27 }tr[MAXN<<2]; 28 struct edge{ 29 int v,nxt; 30 }e[MAXN<<1]; 31 int n,m,cnt,tot; 32 int p[MAXN],head[MAXN],f[MAXN][2]; 33 int fa[MAXN],top[MAXN],bot[MAXN],dfn[MAXN],id[MAXN],size[MAXN],son[MAXN]; 34 void add (int u,int v) 35 { 36 e[++cnt].v=v; 37 e[cnt].nxt=head[u]; 38 head[u]=cnt; 39 } 40 void dfs1 (int u,int ff) 41 { 42 fa[u]=ff;size[u]=1; 43 for (int i=head[u];i!=0;i=e[i].nxt) 44 if (e[i].v!=ff) 45 { 46 dfs1 (e[i].v,u); 47 f[u][0]+=max (f[e[i].v][0],f[e[i].v][1]); 48 f[u][1]+=f[e[i].v][0]; 49 size[u]+=size[e[i].v]; 50 if (size[e[i].v]>size[son[u]]) son[u]=e[i].v; 51 } 52 f[u][1]+=p[u]; 53 } 54 void dfs2 (int u,int topf) 55 { 56 top[u]=topf;bot[u]=u;id[u]=++tot;dfn[tot]=u; 57 if (son[u]) dfs2 (son[u],topf),bot[u]=bot[son[u]]; 58 for (int i=head[u];i!=0;i=e[i].nxt) 59 if (!id[e[i].v]) 60 dfs2 (e[i].v,e[i].v); 61 } 62 void update (int rt) 63 { 64 tr[rt].v=tr[rt<<1].v*tr[rt<<1|1].v; 65 } 66 void build (int rt,int l,int r) 67 { 68 tr[rt].l=l,tr[rt].r=r; 69 if (l==r) 70 { 71 int u=dfn[l],f0=0,f1=p[u]; 72 for (int i=head[u];i!=0;i=e[i].nxt) 73 if (son[u]!=e[i].v&&fa[u]!=e[i].v) 74 { 75 f0+=max (f[e[i].v][0],f[e[i].v][1]); 76 f1+=f[e[i].v][0]; 77 } 78 tr[rt].v.a[1][1]=tr[rt].v.a[1][2]=f0; 79 tr[rt].v.a[2][1]=f1; 80 val[l]=tr[rt].v; 81 return; 82 } 83 int mid=(l+r)>>1; 84 build (rt<<1,l,mid);build (rt<<1|1,mid+1,r); 85 update (rt); 86 } 87 Matrix query (int rt,int l,int r) 88 { 89 if (l<=tr[rt].l&&tr[rt].r<=r) return tr[rt].v; 90 int mid=(tr[rt].l+tr[rt].r)>>1; 91 if (r<=mid) return query (rt<<1,l,r); 92 if (mid<l) return query (rt<<1|1,l,r); 93 else return query (rt<<1,l,r)*query (rt<<1|1,l,r); 94 } 95 void modify (int rt,int pos) 96 { 97 if (tr[rt].l==tr[rt].r) 98 { 99 tr[rt].v=val[tr[rt].l]; 100 return; 101 } 102 int mid=(tr[rt].l+tr[rt].r)>>1; 103 if (pos<=mid) modify (rt<<1,pos); 104 else modify (rt<<1|1,pos); 105 update (rt); 106 } 107 void Modify (int u,int v) 108 { 109 val[id[u]].a[2][1]+=v-p[u];p[u]=v; 110 Matrix pre,nw; 111 while (u) 112 { 113 pre=query (1,id[top[u]],id[bot[u]]); 114 modify (1,id[u]); 115 nw=query (1,id[top[u]],id[bot[u]]); 116 u=fa[top[u]]; 117 val[id[u]].a[1][1]+=max (nw.a[1][1],nw.a[2][1])-max (pre.a[1][1],pre.a[2][1]); 118 val[id[u]].a[1][2]=val[id[u]].a[1][1]; 119 val[id[u]].a[2][1]+=nw.a[1][1]-pre.a[1][1]; 120 } 121 } 122 int main() 123 { 124 n=read ();m=read (); 125 for (int i=1;i<=n;i++) p[i]=read (); 126 for (int i=1;i<n;i++) 127 { 128 int u=read (),v=read (); 129 add (u,v);add (v,u); 130 } 131 dfs1 (1,0);dfs2 (1,1);build (1,1,n); 132 while (m--) 133 { 134 int x=read (),y=read (); 135 Modify (x,y); 136 Matrix ans=query (1,id[top[1]],id[bot[1]]); 137 printf ("%d ",max (ans.a[1][1],ans.a[2][1])); 138 } 139 return 0; 140 }
全局平衡二叉树版本:
1 #include<bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define MAXN 1000010 4 using namespace std; 5 namespace IO 6 { 7 const unsigned int Buffsize=1<<25,Output=1<<25; 8 static char Ch[Buffsize],*St=Ch,*T=Ch; 9 inline char getc() 10 { 11 return((St==T)&&(T=(St=Ch)+fread(Ch,1,Buffsize,stdin),St==T)?0:*St++); 12 } 13 static char Out[Output],*nowps=Out; 14 inline void flush(){fwrite(Out,1,nowps-Out,stdout);nowps=Out;} 15 inline int read() 16 { 17 int x=0;static char ch;int f=1; 18 for(ch=getc();!isdigit(ch);ch=getc())if(ch=='-')f=-1; 19 for(;isdigit(ch);ch=getc())x=x*10+(ch^48); 20 return x*f; 21 } 22 template<typename T>inline void write(T x,char ch=' ') 23 { 24 if(!x)*nowps++=48; 25 if(x<0)*nowps++='-',x=-x; 26 static unsigned int sta[111],tp; 27 for(tp=0;x;x/=10)sta[++tp]=x%10; 28 for(;tp;*nowps++=sta[tp--]^48); 29 *nowps++=ch; 30 } 31 } 32 using namespace IO; 33 struct edge{ 34 int v,nxt; 35 }e[MAXN<<1]; 36 struct Matrix{ 37 int a[2][2]; 38 inline Matrix (){memset (a,0,sizeof (a));} 39 inline Matrix(int A,int B){a[0][0]=a[0][1]=A,a[1][0]=B,a[1][1]=-INF;} 40 inline Matrix (int A,int B,int C,int D){a[0][0]=A,a[0][1]=B,a[1][0]=C,a[1][1]=D;} 41 inline Matrix operator * (const Matrix &b) const 42 { 43 return Matrix (max (a[0][0]+b.a[0][0],a[0][1]+b.a[1][0]),max (a[0][0]+b.a[0][1],a[0][1]+b.a[1][1]),max (a[1][0]+b.a[0][0],a[1][1]+b.a[1][0]),max (a[1][0]+b.a[0][1],a[1][1]+b.a[1][1])); 44 } 45 }F[MAXN],G[MAXN]; 46 int n,m,cnt,root,ans; 47 int val[MAXN],size[MAXN],son[MAXN],top[MAXN],sz[MAXN]; 48 int f[MAXN][2],g[MAXN][2],sum[MAXN],id[MAXN]; 49 int ch[MAXN][2],fa[MAXN],head[MAXN]; 50 inline void add (int u,int v) 51 { 52 e[++cnt].v=v,e[cnt].nxt=head[u],head[u]=cnt; 53 } 54 inline void dfs1 (int u,int ff) 55 { 56 fa[u]=ff,size[u]=1,f[u][1]=val[u]; 57 for (register int i=head[u];i!=0;i=e[i].nxt) 58 if (e[i].v!=ff) 59 { 60 dfs1 (e[i].v,u); 61 size[u]+=size[e[i].v]; 62 f[u][0]+=max (f[e[i].v][0],f[e[i].v][1]); 63 f[u][1]+=f[e[i].v][0]; 64 if (size[e[i].v]>size[son[u]]) son[u]=e[i].v; 65 } 66 sz[u]=size[u]-size[son[u]]; 67 } 68 inline void update (int x) 69 { 70 F[x]=F[ch[x][0]]*G[x]*F[ch[x][1]]; 71 } 72 inline void build (int &x,int l,int r,int Fa) 73 { 74 if (l>r) return; 75 int k=(sum[r]+sum[l-1]+1)>>1,L=l,R=r; 76 while (L<R) 77 { 78 int mid=(L+R)>>1; 79 if (sum[mid]>=k) R=mid; 80 else L=mid+1; 81 } 82 x=id[L]; 83 build (ch[x][0],l,L-1,x); 84 build (ch[x][1],L+1,r,x); 85 fa[x]=Fa,update (x); 86 } 87 inline void dfs2 (int u,int topf) 88 { 89 top[u]=topf; 90 if (son[u]) dfs2 (son[u],topf); 91 g[u][1]=val[u]; 92 for (register int i=head[u];i!=0;i=e[i].nxt) 93 if (e[i].v!=fa[u]&&e[i].v!=son[u]) 94 { 95 dfs2 (e[i].v,e[i].v); 96 g[u][0]+=max (f[e[i].v][0],f[e[i].v][1]); 97 g[u][1]+=f[e[i].v][0]; 98 } 99 G[u]=Matrix (g[u][0],g[u][1]); 100 if (top[u]==u) 101 { 102 int tot=0; 103 for (register int i=u;i!=0;i=son[i]) 104 id[++tot]=i,sum[tot]=sum[tot-1]+sz[i]; 105 build (root,1,tot,fa[u]); 106 } 107 } 108 int main() 109 { 110 srand (time (NULL)); 111 n=read (),m=read (); 112 for (register int i=1;i<=n;i++) val[i]=read (); 113 for (register int i=1;i<n;i++) 114 { 115 int u=read (),v=read (); 116 add (u,v),add (v,u); 117 } 118 int gen=rand ()%n+1; 119 F[0].a[0][1]=F[0].a[1][0]=-INF; 120 dfs1 (gen,0),dfs2 (gen,gen); 121 int x,y,u; 122 while (m--) 123 { 124 x=read ()^ans,y=read (); 125 g[x][1]+=y-val[x],val[x]=y; 126 G[x]=Matrix (g[x][0],g[x][1]); 127 while (x) 128 { 129 u=fa[x]; 130 if (ch[u][0]!=x&&ch[u][1]!=x) 131 { 132 g[u][0]-=max (F[x].a[0][0],F[x].a[1][0]); 133 g[u][1]-=F[x].a[0][0]; 134 } 135 update (x); 136 if (ch[u][0]!=x&&ch[u][1]!=x) 137 { 138 g[u][0]+=max (F[x].a[0][0],F[x].a[1][0]); 139 g[u][1]+=F[x].a[0][0]; 140 G[u]=Matrix (g[u][0],g[u][1]); 141 } 142 x=u; 143 } 144 ans=max (F[root].a[0][0],F[root].a[1][0]); 145 write (ans); 146 } 147 flush (); 148 return 0; 149 }