初步了解二叉堆（二叉堆及其基本操作）

参考资料：《算法竞赛进阶指南》- 李煜东

一.什么是二叉堆

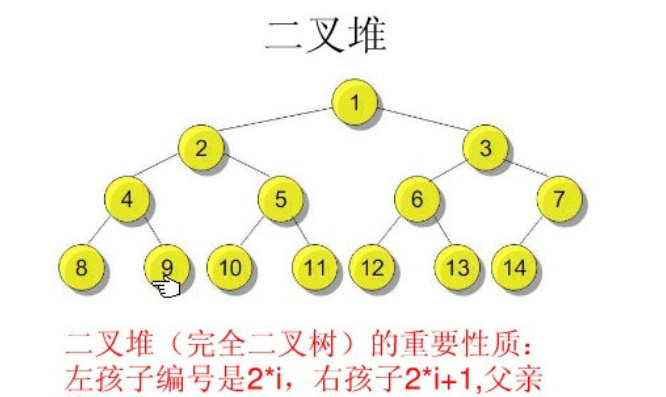
如图，简单来说，二叉堆是一棵满足“堆性质”的完全二叉树，树上的每一个节点都带有一个权值。
若树中任意的一个节点的权值都小于等于其父节点的权值，则称满足该性质的完全二叉树为大根堆（根权值最大）。
若树中任意的一个节点的权值都大于等于其父节点的权值，则称满足该性质的完全二叉树为小根堆（根权值最小）。

二叉树是一种支持插入、删除、查询的数据结构。

二.二叉堆的基本操作

在介绍二叉堆的基本操作之前，我们要先说说如何建堆。

根据完全二叉树的性质，我们可以采用层次序列存储方式，直接用一个数组来保存二叉堆。我们让父节点的编号等于子节点编号除以 2 ，左子节点编号等于父节点编号乘以 2 ，右子节点编号等于父节点编号乘以 2 加 1 。（如上图所示）

接下来，我们以一个大根堆为例，介绍一下二叉堆的基本操作

1.维护二叉堆（Down/Up）

为了保证大根堆满足它的性质，我们有 Down 和 Up 两种操作。
Down 是从某个节点从上往下维护，在某个节点中，如果它的左儿子或右儿子是三个节点中最大的，则应该让最大的与父节点交换。

void down(int p)
{
  int t=p*2;//左儿子
  while(p<=n)
  {
    if(t<n&&heap[p]<heap[p+1])//取子节点中最大的
        t++;
    if(heap[t]>heap[p])
    {
      swap(heap[t],heap[p]);
      p=t,t=2*p;//p到了t的位置，继续循环
    }
    else 
        break;
  }
}

Up 同理，是从下向上维护

void down(int p)
{
  while(p>1)
  {
    if(heap[p/2]<heap[p])
    {
      swap(heap[p/2],heap[p])
      p/=2;
    }
    else 
        break;
  }
}

2.插入一个数（Insert）

如果要向二叉堆中插入一个权值为 val 的点，我们可以直接将它放入堆末尾，然后 Up 维护

void insert（int val）
{
    heap[++n]=val;
    up(n);
}

3.求最大值（GetTop）

int GetTop()
{
  return heap[1];
}

4.删除最大值（Extrat）

即删除堆顶，我们可以将堆顶和堆尾交换，后删除堆尾，然后 Down 操作

void Extrat()
{
   heap[1]=heap[n--];
   down(1);
}

5.删除任意一个元素（Remove）

如果我们要删除 k 元素，可以将它与堆尾交换，后删除堆尾，然后进行 Down 和 Up两个操作（因为被换到中间，向上向下调整都有可能）

void remove(int k)
{
   heap[k]=heap[n--];
   up(k),down(k);
}

6.修改任意一个元素（Change）

void change(int k,int x)
{
   heap[k]=x;
   up(k),down(k);
}

三.例题（AcWing 838 堆排序）

原题

这题就运用到了上面四个基本操作，值得注意的是，我们开始应该如何建堆？我们可以对 n/2 到 1 的节点进行 Down 操作（因为叶节点没有子节点，就不用枚举了），也可以从 2 到 n 进行 Up 操作，这样我们可以在 O(n) 时间内维护一个二叉堆。

时间复杂度的证明是一个等差比数列的求和，这个和小于1，所以为 O(n)。

应注意的是，这题是维护一个小根堆，所以上面操作应该有所修改。

代码：

#include<bits/stdc++.h>
using namespace std;
int heap[100005],n,x,m,a[1000005];
void down(int p)
{
  int t=p*2;
  while(t<=n)
  {
    if(t<n&&heap[t]>heap[t+1])
        t=t+1;
    if(heap[t]<heap[p])
    {
        swap(heap[t],heap[p]);
        p=t,t=p*2;
    }
    else
        break;
  }

}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
      cin>>heap[i];
    }
    for(int i=n/2;i;i--)
    {
      down(i);
    }
    while(m--)
    {
      printf("%d ",heap[1]);//每次取出堆顶
      heap[1]=heap[n--];
      down(1);
    }
return 0;
}

四.STL 优先队列

可以说优先队列和二叉堆有着相同的性质，而在C++中由于priority_queue的存在，为我们上述的几个操作提供了极大的便利，有现成的函数可以拿来使用，所以下面就来简单介绍一下。

头文件：#include<queue>

该STL语法除了大多数STL支持的 heap.size() ， heap.empty() 之外，还有以下几个

1.建立优先队列

priority_queue<int>heap;//默认为大根堆

如果想要实现一个小根堆，有两种方法：

① 直接在插入元素时以相反数插入，这样就实现了越“小”的数越在上面，记得取出后要还原

② 建优先队列时做修改

priority_queue<int,vector<int>,greater<int>>heap;//小根堆

2.把元素插入 O(logn)

heap.push(x);

3.删除堆顶元素 O(logn)

heap.pop();

4.查询堆顶元素 O(1)

int x=heap.top();

注意：queue 没有 heap.clear() 操作