2019-08-22 纪中NOIP模拟A&B组

T1 [JZOJ3229] 回文子序列

题目描述

　　回文序列是指左右对称的序列。我们会给定一个N×M的矩阵，你需要从这个矩阵中找出一个P×P的子矩阵，使得这个子矩阵的每一列和每一行都是回文序列。

数据范围

　　对于 $20\%$ 的数据，$1 leq N,M leq 10$

　　对于 $100\%$ 的数据，$1 leq N,M leq 300$

分析

　　$O(n^5)$ 暴力跑起来真实快

#include <iostream>
#include <cstdio>
#include <cstdlib> 
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 305

int n, m, flag;
int g[N][N];

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            scanf("%d", &g[i][j]);
    for (int k = min(n, m); k; k--)
        for (int x = 1; x + k - 1 <= n; x++)
            for (int y = 1; y + k - 1 <= m; y++) {
                flag = 1;
                for (int i = 0; i < k; i++) {
                    for (int j = 1; j <= k / 2; j++)
                        if (g[x + i][y + j - 1] != g[x + i][y + k - j] ||
                            g[x + j - 1][y + i] != g[x + k - j][y + i]) {
                            flag = 0; break;
                        }
                    if (!flag) break;
                }
                if (flag) {printf("%d", k); return 0;}
            }
    
    return 0;
}

T2 [JZOJ3230] 树环转换

题目描述

　　给定一棵N个节点的树，去掉这棵树的一条边需要消耗值1，为这个图的两个点加上一条边也需要消耗值1。树的节点编号从1开始。在这个问题中，你需要使用最小的消耗值（加边和删边操作）将这棵树转化为环，不允许有重边。

　　环的定义：（1）该图有N个点，N条边。（2）每个顶点的度数为2。（3）任意两点是可达的。

　　树的定义：（1）该图有N个点，N-1条边。（2）任意两点是可达的。

数据范围

　　对于 $20\%$ 的数据，$1 leq N leq 10$

　　对于 $100\%$ 的数据，$1 leq N leq 10^6$

分析

　　看到这种树状的题，很容易能想到树形 $dp$

　　我们发现当环删去一条边时，就变成了一棵特殊的树——链

　　所以考虑找出将树转化为一条链的最小代价，最后答案加一

　　设 $f[x][0]$ 表示 $x$ 的子树转化为链且一个端点为 $x$ 时的最小代价，$f[x][1]$ 表示 $x$ 的子树转化为链（不考虑 $x$ 在链上的位置）的最小代价

　　对于 $f[x][1]$，有两种转移方式

　　

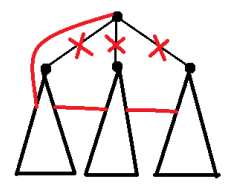
　　令 $Sum$ 为 $sum_{son} f[son][1]$，$Cnt$ 为 $x$ 的子节点数，则有 $$f[x][0]=min(Sum+2Cnt,Sum-(f[u][1]-f[u][0])+2(Cnt-1))$$

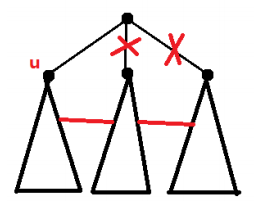
　　对于 $f[x][0]$，$f[x][1]$ 当然属于其一种情况，此外还一种情况

　　

　　此时状态转移方程为 $$f[x][1]=min(f[x][0],Sum-(f[p][1]-f[p][0])-(f[q][1]-f[q][0])+2(Cnt-2))$$

　　为了得到点 $x$ 的 $u,p,q$，只需要记录其子节点中 $f[son][1]-f[son][0]$ 的最大值与次大值

　　由于数据对 $dfs$ 不是很友好，最后一个点会爆栈，所以我选择手写栈

　　当然也可以选择 $bfs$ 或者贪心

　　说到贪心，就是不停找两端点的度都大于 $2$ 的边删去，AC代码里跑得最快的是这么写的，感觉有点道理（然而这个贪心不存在完全正确性，结果会因遍历顺序产生不同）

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 1000005

int n, uu, vv, tot, top;
int f[N][2], stack[N], cur[N];
int to[N << 1], nxt[N << 1], head[N];

inline void add(int u, int v) {
    to[++tot] = v; nxt[tot] = head[u]; head[u] = tot;
}

void dfs() {
    memcpy(cur, head, sizeof cur);
    while (top) {
        int x = stack[top], go = 0;
        for (int i = cur[x]; i; i = nxt[i])
            if (to[i] != stack[top - 1]) {
                cur[x] = nxt[i]; stack[++top] = to[i];
                go = 1; break;
            }
        if (go) continue;
        int m1 = -inf, m2 = -inf, sum = 0, cnt = 0;
        for (int i = head[x]; i; i = nxt[i]) {
            if (to[i] == stack[top - 1]) continue;
            int now = f[to[i]][1] - f[to[i]][0];
            if (now > m1) m2 = m1, m1 = now;
            else if (now > m2) m2 = now;
            sum += f[to[i]][1]; cnt++;
        }
        if (cnt) {
            f[x][0] = min(sum + 2 * cnt, sum - m1 + 2 * (cnt - 1));
            f[x][1] = min(f[x][0], sum - m1 - m2 + 2 * (cnt - 2));
        }
        top--;
    }
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i < n; i++) {
        scanf("%d%d", &uu, &vv);
        add(uu, vv); add(vv, uu);
    }
    stack[++top] = 1; dfs();
    printf("%d", f[1][1] + 1);
    
    return 0;
}

T3 [JZOJ3231] 海明距离

题目描述

　　对于二进制串a，b，他们之间的海明距离是指两个串异或之后串中1的个数。

　　计算两个串之间的海明距离的时候，他们的长度必须相同。现在我们给出N个不同的二进制串，请计算出这些串两两之间的最短海明距离。

　　（输入时每个二进制串用一个长度为5的16进制串表示）

数据范围

　　对于 $30\%$ 的数据，$1 leq N leq 100$

　　对于 $100\%$ 的数据，$1 leq N leq 10^5$

分析

　　我们可以从小到大枚举海明距离，与该海明距离下的所有可能的异或结果

　　对于一个异或结果，我们可以枚举给定的二进制串，如果该异或结果与该串异或后得到的二进制数也是一个给定的串，那么当前的海明距离是存在的，就可以直接得出答案

　　这样做的理论时间复杂度为 $O(20 imes 2^{20}n)$，但实际上不可能同时达到 $ans=20$，$n=10^5$，因为这些二进制串两两之间互不相同，当 $ans=20$ 时，$n$ 一定为 $2$，以此类推，这个时间复杂度是远远跑不满的

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 100005
#define M (1 << 20) + 5

int t, n, ans;
int a[N], book[M], cnt[M];
char c;

int main() {
    scanf("%d", &t);
    for (int i = 0, j = i; i < (1 << 20); j = ++i)
        while (j) j &= (j - 1), cnt[i]++;
    while (t--) {
        scanf("%d", &n);
        memset(a, 0, sizeof a);
        memset(book , 0, sizeof book);
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= 5; j++) {
                scanf(" %c", &c);
                if (isdigit(c)) a[i] = a[i] * 16 + c - '0';
                else a[i] = a[i] * 16 + 10 + c - 'A';
            }
            book[a[i]] = 1;
        }
        int flag = 0;
        for (ans = 1; ans <= 20; ans++) {
            for (int s = 0; s < (1 << 20); s++)
                if (cnt[s] == ans) {
                    for (int i = 1; i <= n; i++)
                        if (book[s ^ a[i]]) {
                            flag = 1; break;
                        }
                    if (flag) break;
                }
            if (flag) break;
        }
        printf("%d
", ans);
    }
    
    return 0;
}

T4 [JZOJ3232] 排列

题目描述

　　一个关于n个元素的排列是指一个从{1, 2, …, n}到{1, 2, …, n}的一一映射的函数。这个排列p的秩是指最小的k，使得对于所有的i = 1, 2, …, n，都有p(p(…p(i)…)) = i（其中，p一共出现了k次）。

　　例如，对于一个三个元素的排列p(1) = 3, p(2) = 2, p(3) = 1，它的秩是2，因为p(p(1)) = 1, p(p(2)) = 2, p(p(3)) = 3。

　　给定一个n，我们希望从n!个排列中，找出一个拥有最大秩的排列。例如，对于n=5，它能达到最大秩为6，这个排列是p(1) = 4, p(2) = 5, p(3) = 2, p(4) = 1, p(5) = 3。

　　当我们有多个排列能得到这个最大的秩的时候，我们希望你求出字典序最小的那个排列。对于n个元素的排列，排列p的字典序比排列r小的意思是：存在一个整数i，使得对于所有j < i，都有p(j) = r(j)，同时p(i) < r(i)。对于5来说，秩最大而且字典序最小的排列为：p(1) = 2, p(2) = 1, p(3) = 4, p(4) = 5, p(5) = 3。

数据范围

　　对于 $40\%$ 的数据，$1 leq N leq 100$

　　对于 $100\%$ 的数据，$1 leq N leq 10^4$

分析

　　这题很像 2019 - 08 - 09 - T3

　　这里是要求将 $n$ 分为若干数之和，使得这些数的最小公倍数最大

　　然后就是做质数幂之积最大的多重背包了

　　但这里的 $f$ 会很大，远超 $long ; long$ 的范围，所以可以将 $f$ 中的元素用自然对数表示

　　最后显然就是把小的循环节放在前面，并且每个循环节中把第一个数放到节末输出

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
using namespace std;
#define ll long long
#define inf 0x3f3f3f3f
#define N 10005

int T, n, m, last;
int vis[N], p[N], t[N];
pair<int, int> pre[1300][N];
double f[2][N], Log[N];

int main() {
    scanf("%d", &T);
    for (int i = 2; i <= N; i++) {
        if (!vis[i]) p[++p[0]] = i;
        for (int j = 1; j <= p[0]; j++) {
            if (i * p[j] > N) break;
            vis[i * p[j]] = 1;
        }
    }
    for (int i = 2; i <= N; i++) Log[i] = log(i);
    while (T--) {
        scanf("%d", &n);
        if (n == 1) {printf("1
"); continue;}
        for (int i = 0; i <= n; i++) f[0][i] = 0;
        for (int i = 1; i <= p[0] && p[i] <= n; m = i, i++)
            for (int j = n; j >= p[i]; j--) {
                f[i & 1][j] = f[(i & 1) ^ 1][j];
                pre[i][j] = pre[i - 1][j];
                for (int k = p[i]; k <= j; k *= p[i])
                    if (f[i & 1][j] < f[(i & 1) ^ 1][j - k] + Log[k]) {
                        f[i & 1][j] = f[(i & 1) ^ 1][j - k] + Log[k];
                        pre[i][j] = make_pair(i - 1, j - k);
                    }
            }
        t[0] = last = 0;
        while (m && n) {
            int x = pre[m][n].first;
            int y = pre[m][n].second;
            t[++t[0]] = n - y;
            m = x; n = y;
        }
        while (n--) t[++t[0]] = 1;
        sort(t + 1, t + t[0] + 1);
        for (int i = 1; i <= t[0]; i++) {
            for (int j = 2; j <= t[i]; j++)
                printf("%d ", last + j);
            printf("%d ", last + 1);
            last += t[i];
        }
        printf("
");
    }
    
    return 0;
}