常用的概率分布:伯努利分布、二项式分布、多项式分布、先验概率，后验概率

一，伯努利分布(bernouli distribution)

---

又叫做0-1分布，指一次随机试验，结果只有两种。也就是一个随机变量的取值只有0和1。
记为: 0-1分布 或B(1,p)，其中 p 表示一次伯努利实验中结果为正或为1的概率。 

概率计算：

P(X=0)=p0P(X=1)=p1

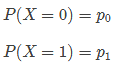
期望计算：

E(X)=0∗p0+1∗p1=p

最简单的例子就是，抛一次硬币，预测结果为正还是反。

二，二项式分布(binomial distrubution)

---

表示n次伯努利实验的结果。

记为：X~B(n,p)，其中n表示实验次数，p表示每次伯努利实验的结果为1的概率，X表示n次实验中成功的次数。
概率计算：

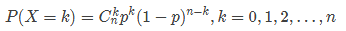
期望计算：

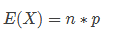
例子就是，求多次抛硬币，预测结果为正面的次数。

三，多项式分布(multinomial distribution)

---

多项式分布是二项式分布的扩展，不同的是多项式分布中，每次实验有n种结果。
概率计算：

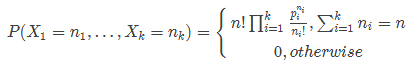
期望计算：

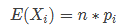
最简单的例子就是多次抛筛子，统计各个面被掷中的次数。

四，先验概率，后验概率，共轭分布

---

先验概率和后验概率 ：

　　先验概率和后验概率的概念是相对的，后验的概率通常是在先验概率的基础上加入新的信息后得到的概率，所以也通常称为条件概率。比如抽奖活动，5个球中有2个球有奖，现在有五个人去抽，小名排在第三个，问题小明抽到奖的概率是多少？初始时什么都不知道，当然小明抽到奖的概率P( X = 1 ) = 2/5。但当知道第一个人抽到奖后，小明抽到奖的概率就要发生变化，P(X = 1| Y₁ = 1) = 1/4。

　　再比如自然语言处理中的语言模型，需要计算一个单词被语言模型产生的概率P(w)。没有看到任何语料库的时候，我们只能猜测或者平经验，或者根据一个文档中单词w的占比，来决定单词的先验概率P(w) = 1/1000。之后根据获得的文档越多，我们可以不断的更新

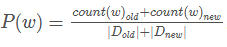。也可以写成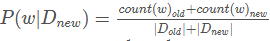。再比如，你去抓娃娃机，没抓之前，你也可以估计抓到的概率，大致在1/5到1/50之间，它不可能是1/1000或1/2。然后你可以通过投币，多次使用娃娃机，更据经验来修正，你对娃娃机抓到娃娃的概率推断。后验概率有时候也可以认为是不断学习修正得到的更精确，或者更符合当前情况下的概率。

共轭分布 ：

　　通常我们可以假设先验概率符合某种规律或者分布，然后根据增加的信息，我们同样可以得到后验概率的计算公式或者分布。如果先验概率和后验概率的符合相同的分布，那么这种分布叫做共轭分布。共轭分布的好处是可以清晰明了的看到，新增加的信息对分布参数的影响，也即概率分布的变化规律。

 原文：https://www.cnblogs.com/tianqizhi/p/9746135.html

参考：https://blog.csdn.net/u010138758/article/details/70158642