问题描述： 给定n个物品和一个背包，物品i的重量为Wi，价值为Vi，背包的容量为c。求如何选择装入背包的物品使得装入的物品总价值最大。
要解决这个问题，我们要从上到下来解决。我用例题来说明吧。。。（算法这个东西写出来是真的难。。。。）
算法详解：
这里我们直接给出递推方程：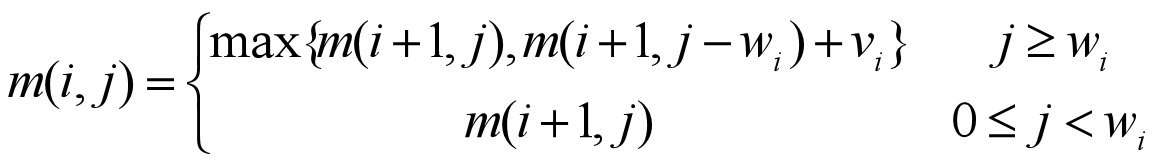
这里的m矩阵中有两个变量M[i][j]，其中i表示当前处理的物品为i，j表示当前背包中能存入的最大的容量。
①j<wi时，意思是当当前背包可装入的容量<第i个物品的重量时，我这个物品肯定装不进去呀对不对。所以所以第i个物品不装进去，此时m[i][j]中存入的最优解为上一个m[i+1][j]。
②i>wi时，我们要分两种情况，第一是放入当前的这个第i个物品（要加上第i个物品的价值），第二种情况是不放入第i个物品。比较大小取最大值。
例题：
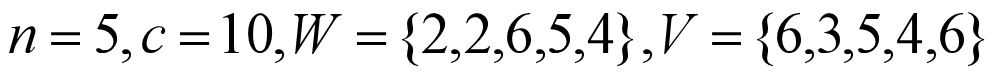
这里一共有5个物品，背包的总重量为10，每个物品的重量分别为｛2 2 6 5 4｝ 每个物品的价值为｛6 3 5 4 6｝。
这里我们要用一个二维矩阵来处理问题：
我们在填写这个表格的时候是先从第五行开始依次向上。因为第五个数的重量是4，所以[5,0]到[5,3]均为0（因为放不下。。。）后面[5,4]到[5,10]全是6。
之后填写第四行，第四个物品的重量为5，所以5之前背包中是不够放第四个物品的，所以原样把下面的值誊写过去。从[4,5]开始，我们可以分两种情况 ①对于[4,5]这个空格，我们可以分为 [5,0]+4=4与[5,5] =6 所以选择6写到这个格子里。
在最后一行中，我们不用考虑前面的数，只用考虑最后一个[1,10]就好。因为我们要求得最大容量的背包最大值，而要求这个解只用到下一行的数据，不需要用同一行的数据。
得到[1,10]=max([2,10],[2,8]+6) 得到[2,8]+6=15>11 将第1个数装入背包。
由此我们根据箭头可以得到。[1,10]是由[2,8]得到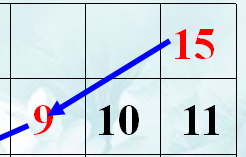
，所以第一个物品装入。
[2,8]是由[3,6]得来，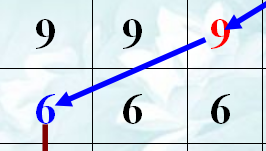
所以 第二个物品装入。
[3,6]是由[4,6]得来的
，说明第三个物品没有装入。同理第四个物品没装入。
而第五个物品装入后得到的6，所以第五个物品装入了。
最后得到最后的解为(1,1,0,0,1)。
动态规划01背包的问题就在于这个矩阵的填写，所以我们要理解出来这个过程。代码这里就不详细写了，大家可以查一查。有什么要交流的地方大家给我留言哈~
再次感谢老师的课件。。。。
————————————————————————————————————————Made By Pinging