题目链接:
http://poj.org/problem?id=1113
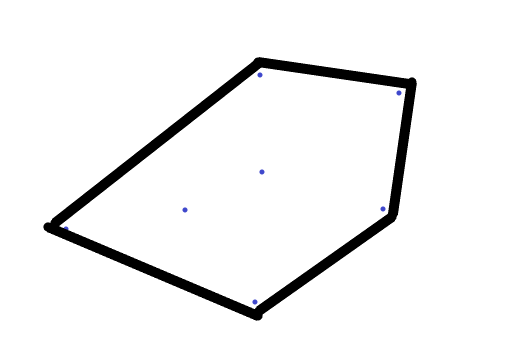
求下列点的凸包

求得凸包如下:
Graham扫描算法:
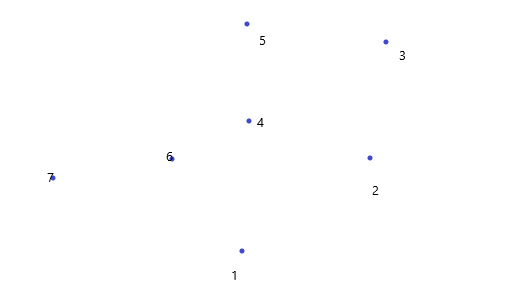
找出最左下的点,设为一号点,将其它点对一号点连线,按照与x轴的夹角大小排序:
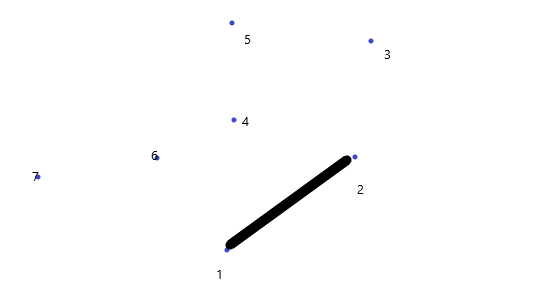
让点1,2入栈,从第三个点开始循环
步骤1:判断该点是否在栈顶第二个点和栈顶的点的连线的左边,
2.如果在左边,将该点入栈,继续循环,
3.如果不在,弹出栈顶点,重复步骤1,
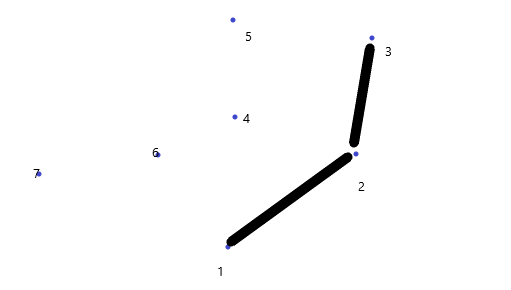
3在1,2连线左边,3入栈
4在2,3连线左边,4入栈
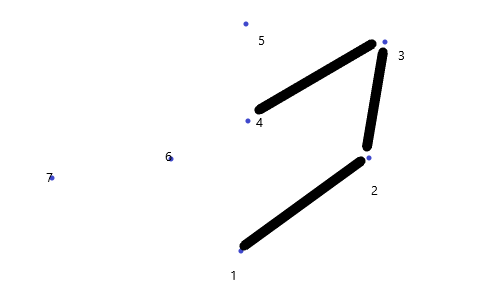
5不在3,4连线左边,4出栈,5在2,3连线左边,5入栈
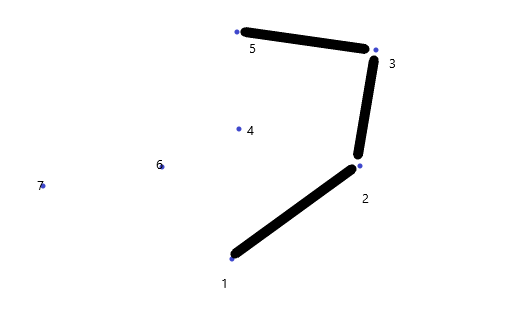
6在3,5连线左边,6入栈
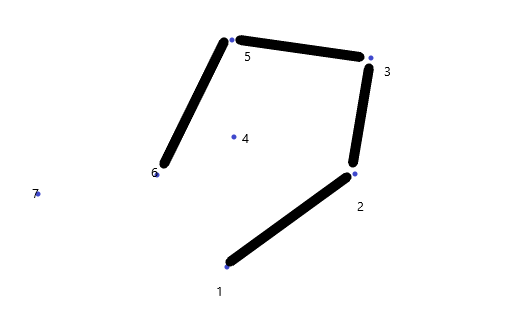
7不在5,6连线左边,6出栈,7在3,5连线左边,7入栈
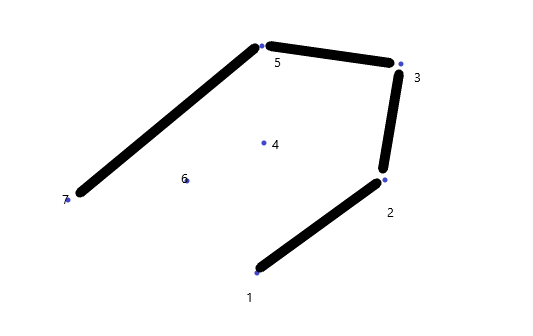
遍历完成后,将栈顶与1连起来就完成了
代码
//#include<bits/stdc++.h> #include<iostream> #include<cmath> #include<algorithm> #define fi first #define se second #define INF 0x3f3f3f3f #define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0) #define pqueue priority_queue #define NEW(a,b) memset(a,b,sizeof(a)) #define lowbit(x) ((x)&(-x)) using namespace std; const double pi=4.0*atan(1.0); const double e=exp(1.0); const int maxn=4e4+8; typedef long long LL; typedef unsigned long long ULL; const LL mod=1e9+7; const ULL base=1e7+7; struct Point{ int x,y; bool operator<(Point &u){//坐标排序 if(x!=u.x) return x<u.x; return y<u.y; } }; Point vex[maxn],Stack[maxn],Basis; short checkL(Point p,Point q,Point s){//判断点s是否在直线pq的左侧 int area2=p.x*q.y-p.y*q.x+q.x*s.y-q.y*s.x+s.x*p.y-s.y*p.x; if(area2>0) return 1;//表示在左侧 if(area2==0) return 0;//表示在同一条线上; return -1;//表示在右侧 } double dis(Point u,Point v){//计算uv的距离 return sqrt((u.x-v.x)*(u.x-v.x)*1.0+(u.y-v.y)*(u.y-v.y)); } bool cmp(Point a,Point b){//极角排序 short m=checkL(Basis,a,b); if(m==1) return 1;//b在基点与a的连线的左侧,说明b的极角大于a if(m==0&&dis(Basis,a)<=dis(Basis,b))//极角相同时,靠近基点的排在前 return 1; return 0; } int main(){ cin.tie(0); cout.tie(0); int n,l; cin>>n>>l; for(int i=0;i<n;i++){ cin>>vex[i].x>>vex[i].y; } sort(vex,vex+n); Basis=vex[0];//选第一个点为基点 sort(vex+1,vex+n,cmp); int top=0; Stack[top]=vex[0]; Stack[++top]=vex[1]; for(int i=2;i<n;i++){ while(top>=1&&checkL(Stack[top-1],Stack[top],vex[i])<0){ top--; } Stack[++top]=vex[i]; } double sum=0.0; for(int i=0;i<top;i++){ sum+=dis(Stack[i],Stack[i+1]); } sum+=dis(Stack[top],Stack[0]); sum+=2.0*pi*l; LL ans=(LL)sum; if(sum-(double)ans>=0.5){ ans++; } cout<<ans<<endl; system("pause"); return 0; }