hdu5652 India and China Origins(并查集)

India and China Origins

 

 Accepts: 49

 

 Submissions: 426

 Time Limit: 2000/2000 MS (Java/Others)

 

 Memory Limit: 65536/65536 K (Java/Others)

问题描述

很久以前，中国和印度之间并没有喜马拉雅山相隔，两国的文化交流很频繁。随着喜马拉雅山海拔逐渐增加，两个地区的交流也越来越少，最终没有了来往。

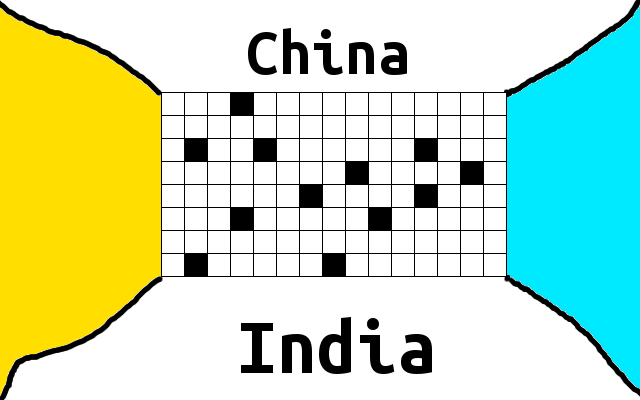
假设当时的地形和我画的一样，蓝色部分代表海洋，而且当时人们还没有发明轮船。黄色部分代表沙漠，而且沙漠上经常有野鬼散步，所以人们不敢到沙漠中行走。黑色的格子表示山峰，这些山峰都无比高大，所以人无法穿过。白色格子代表平原，人可以在平原上自由行走。人每次可以向相邻的四个格子走动。

此外，我们的考古学家发现还有一些山峰会逐渐形成，通过研究发现，位置在 $(x,y)$ （保证该位置之前没有山峰）的地方在 $i$ 年后出现了山峰。现在给你若干个位置出现山峰的时间，你可以计算出中国和印度之间的联系最早被彻底切断的时间吗？

输入描述

多组测试数据, 第一行为组数$T(T\le 10)$。每组测试数据第一行包含两个数 $N,M(1\le N,M\le 500)$, 表示地图的大小。接下来 $N$ 行长度为 $M$ 的 $01$ 字符串。$0$代表白色格子，$1$ 代表山峰。接下来有 $Q(1\le Q\le N\times M)$ 行，第 $i(1\le i\le Q)$ 两个整数 $(x,y),0\le x<N,0\le y<M$ 表示在第 $i$ 年 $(x,y)$ 出现了一座山峰。

输出描述

对于每组测试数据，输出一个数, 表示两国最早失联的时间。如果最终两国之间还有联系则输出 -1。

输入样例

1
4 6
011010
000010
100001
001000
7
0 3
1 5
1 3
0 0
1 2
2 4
2 1

输出样例

4

Hint

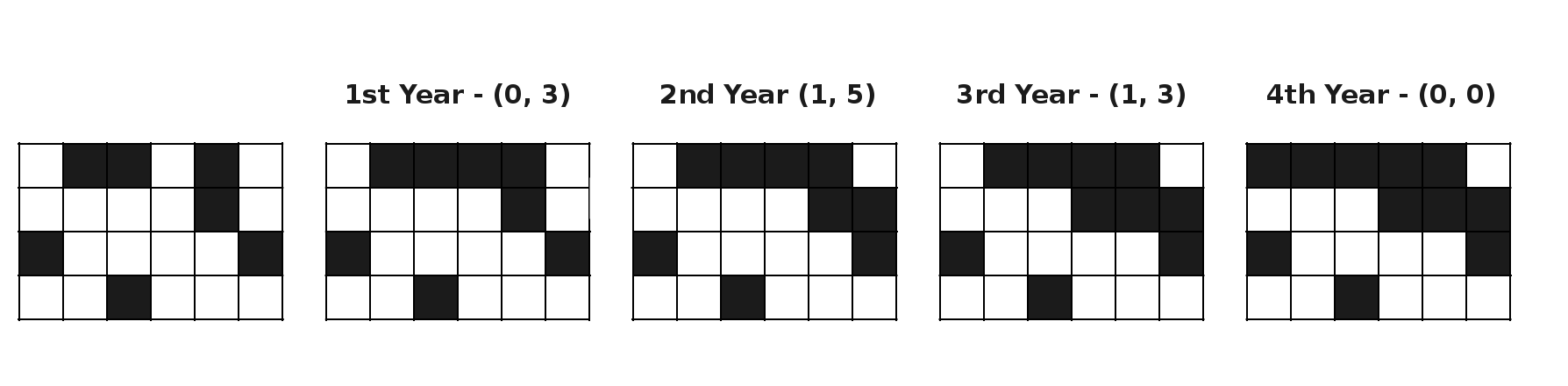
从上图可以看到，两国在第四年彻底失去了联系。

/*
hdu5652 India and China Origins(并查集)

给你一个棋盘形状的东东,上面1代表无法越过的山峰,0代表可以通过的平原.
而且在接下来q次会出现一些山峰,问多少次后棋盘上下不连通
如果一直联通则输出-1

开始想到了并查集但是实现起来有点问题,每次插入后都要把最左边一列判断
一下,看他们的父亲是否是棋盘的最右端.感觉并不够简便
然后参考了下大神们的代码,发现可以在合并的时候记录下这个联通量最左边
和最右边的位置,这样每次合并时只需要判断max-min是否等于棋盘的宽度就
好了
果然自己太死板了TAT

hhh-2016-03-27 12:42:45
*/

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<functional>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 505 ;
int from = 500*500;
int to = 500*500+1;
int n,m;
int dir[9][2] = {{1,1},{1,0},{0,1},{1,-1},{0,-1},{-1,1},{-1,-1},{-1,0}};
char str[maxn];
int far[maxn*maxn];
int tmap[maxn][maxn];
int l[maxn*maxn],r[maxn*maxn];

int fin(int x)
{
    return x == far[x]?  x : far[x] = fin(far[x]);
}

bool  unio(int a,int b)
{
    int ta = fin(a);
    int tb = fin(b);
    if(ta != tb)
    {
        far[ta] = tb;
        l[tb] = min(l[ta],l[tb]);
        r[tb] = max(r[ta],r[tb]);
        if(r[tb] - l[tb] == m-1)
            return 1;
    }
    return 0;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i = 0; i < n; i++)
        {
            scanf("%s",str);
            for(int j = 0; j < m; j++)
            {
                tmap[i][j] = str[j]-'0';
                far[i*m+j] = i*m+j;
            }
        }

        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
                //if(tmap[i][j])
                {
                    l[i*m+j] = j;
                    r[i*m+j] = j;
                }
        }
        int flag =0;
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                if(tmap[i][j])
                {
                    for(int k = 0; k < 8; k++)
                    {
                        int tx = i + dir[k][0];
                        int ty = j + dir[k][1];
                        if(tx < 0 || tx >= n || ty < 0 || ty >= m || !tmap[tx][ty])
                            continue;
                        if(unio(i*m+j,tx*m+ty))
                            flag = 1;
                    }

                }
            }
        }
        if(flag)
            printf("0
");
        int q;
        scanf("%d",&q);
        for(int i = 0; i < q; i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            tmap[x][y] = 1;
            if(flag)
                continue;
            for(int k = 0; k < 8; k++)
            {
                int tx = x + dir[k][0];
                int ty = y + dir[k][1];
                if(tx < 0 || tx >= n || ty < 0 || ty >= m || !tmap[tx][ty])
                    continue;
                if(unio(x*m+y,tx*m+ty))
                {
                    flag = 1;
                    printf("%d
",i+1);
                }
            }
        }
        if(!flag)
            printf("-1
");
    }
    return 0 ;
}