LDU-五一假期专练（5.1）

目录

• • J - Cunning Friends
  • F - Binary Transformations
  • A - Concerts

J - Cunning Friends

博弈论：

题目大意：给出n个桶每个桶里面都有若干个小球，三个人做游戏，先手先进行操作，剩下的两个人是一伙的，想让先手输掉，三个人轮流进行游戏，每个人选一个桶取出 > 0 个球，当一个人无法进行操作的时候，就输掉了
后面的两个人想让先手输掉，问先手能否赢得比赛

打表找规律：

typedef int itn;
int n, m;
int eq, da, xiao;
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x = read;
		if (x > 2) da++;
		else if (x == 2) eq++;
		else xiao++;
	}
	if (da == 1) da--, eq++;
	if (da > 1) puts("Lose");
	else if (eq > 2) puts("Lose");
	else if (eq == 1) puts("Win");
	else {
		if (xiao % 3) puts("Win");
		else puts("Lose");
	}
	return 0;
}

/*
2 10
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
AB
ABBBBABBBB

10
*/

F - Binary Transformations

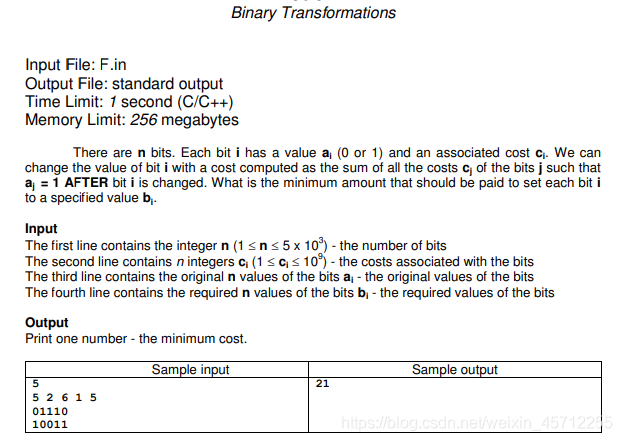
思维贪心
首先说一种错误的贪心策略：
先将所有的应该由1->0的部分进行转换，然后将所有的0->1的部分进行转换
在将1-> 0的过程中，按照权值从大到小进行处理；
在将0-> 1的过程中，按照权值从小到大进行处理；
这样在某些情况下可能是最优的

但是 当有某一个位置两位都是1，并且权值非常非常大的时候，我们首先可以先将这个数转换为0，然后再进行上述操作，还有一点，如果这种情况有若干个位置都有，那么应该转换那一部分 ？换一种说法就是我们应该转换都少个才能满足贪心上的最优呢？
因为在上面两个位置都对应 1 的情况下，转换为0也是有代价的！

这里给出思路来源，能够很好的解决这种情况 博客链接
做法：如果不存在一个位置p (a[p]=1,b[p]=1)，那么答案就是贪心的先把所有的1，按价值从大到小变为0,所有的0,按价值从小到大变为1。如果存在一些位置p，我们就枚举一开始把多少p转成0,显然价值越大的p越优。现在考虑如何模拟，我们可以用2个set，一个维护一开始要从0变1的数，另一个维护最后要由1变0的数，插入O(log n)，遍历O(n)，总的复杂度O(n²)

下面是个人的理解：
因为有两位都是1的情况变换会对答案产生贡献，所以说在考虑这里插入两位都是1的情况
在前面就已经提到过，将1->0的过程中，要按照从大到小的顺序进行，但是再用set维护的过程中，默认的顺序是从小到大，所以就要采用一个逆向的迭代器；而将0->1的过程中是按照从小到大的顺序来进行操作的，用迭代器遍历就ok
因为考虑两位值都是1的情况的时候，代价越大就可能会对答案产生较大的贡献，在插入的过程中，所以要考虑从大到小的顺序
然后维护一下操作的贡献，记录下最小值

typedef int itn;
int n;
ll a[maxn];
string s,t; 
ll sum = 0,ans = 0;
vector<ll> vet;
multiset<ll> st1,st2;
bool cmp(ll a,ll b){
	return a > b;
}
ll get(int x){
	ll ret = 0;
	ll s = sum;
	int pos = x;
	if(pos) st1.insert(vet[pos-1]),st2.insert(vet[pos-1]);
	multiset<ll> :: iterator it1;
	multiset<ll> :: reverse_iterator it2;
	/// 1-> 0  big -> small
	for(it2 = st1.rbegin();it2 != st1.rend();++it2){
		s -= *(it2);
		ret += s;
	}
	for(it1 = st2.begin();it1 != st2.end(); ++ it1){
		s += *(it1);
		ret += s;
	}
	return ret;
}
int main() {
	cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i];
	cin >> s;
	cin >> t;
	s = "#" + s;
	t = "#" + t;
	for(int i=1;i<=n;i++){
		if(s[i] == '1') sum += a[i];
		if(s[i] != t[i]) {
			if(s[i] == '1') st1.insert(a[i]);
			else st2.insert(a[i]);
		}else if(s[i] == '1'){
			vet.push_back(a[i]);
		}
	}
	sort(vet.begin(),vet.end(),cmp);
	int siz = vet.size();
	ll ans = inf;
	// cout <<"ans :  " << ans <<endl;
	for(itn i=0;i<=siz;i++){
		ans = min(ans,get(i));
	}
	cout << ans <<endl;
	return 0;
}

A - Concerts

题面：

dp
首先这个题目的数据范围是有点问题的，codeforces官方声明了更改了之后的数据范围：
Announcement
1 <= k <= 300 1 <= n <= 10^5
题意：
给出两个由大写字母组成的字符序列A,B，在B中找到序列A，还应满足对应的两个字符之间的距离（题目输入）能够满足条件，求方案数
通过数据范围来看应该是可以进行二维的dp,
我们使用dp[i][j] 表示状态：A已经匹配i个位置，当前位置是在j ，当匹配成功的时候，可以发现
dp[i][j] == dp[i][j] + dp[i-1][j-val[i]-1]
匹配不成功的时候，可以发现
dp[i][j] == dp[i][j] + dp[i-1][j]

int n, m;
char a[maxn];
char b[maxn];
int val[30];
int dp[307][maxn];
int main() {
	// n < m -> n 300 m 1e5;
	cin >> n >> m;
	for (itn i = 1; i <= 26; i++) val[i] = read;
	cin >> a + 1;
	cin >> b + 1;
	for (int i = 1; i <= m; i++) { // len of b
		if (a[1] == b[i])
			dp[1][i] = 1;
	}
	for (itn i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			if (a[i] == b[j]) {
				// 匹配成功
				int t = a[i - 1] - 'A' + 1; // 'A' == 64 + 1
				if (j - val[t] - 1 >= 1)
					dp[i][j] += dp[i - 1][j - val[t] - 1], dp[i][j] %= mod;
			}
			dp[i][j] += dp[i][j - 1];
			dp[i][j] %= mod;
		}
	}
	cout << dp[n][m] % mod << endl;
	return 0;
}

/*
2 10
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
AB
ABBBBABBBB

10
*/