数据结构开发(22)：二叉树的转换、深层特性与存储结构设计

0.目录

1.树到二叉树的转换

2.二叉树的深层特性

3.二叉树的存储结构设计

4.小结

1.树到二叉树的转换

通用树结构的回顾：

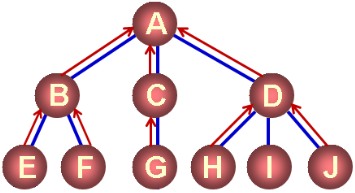
• 双亲孩子表示法
  1. 每个结点都有一个指向其双亲的指针
  2. 每个结点都有若干个指向其孩子的指针

另一种树结构模型：

• 孩子兄弟表示法
  1. 每个结点都有一个指向其第一个孩子的指针
  2. 每个结点都有一个指向其第一个右兄弟的指针

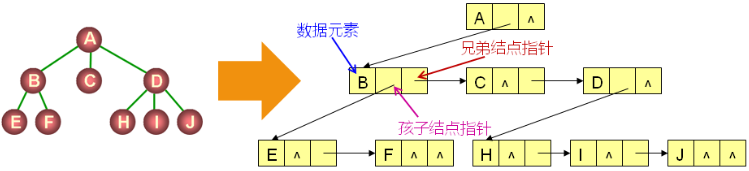
孩子兄弟表示法的特点：

1. 能够表示任意的树形结构
2. 每个结点包含一个数据成员和两个指针成员
3. 孩子结点指针和兄弟结点指针构成了“树权”

二叉树的定义：

• 二叉树是由 n ( n ≥ 0 ) 个结点组成的有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

二叉树的5种形态：

特殊的二叉树：

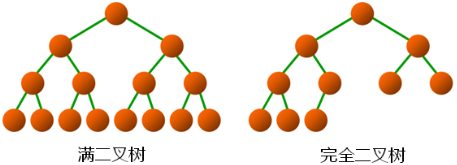
• 满二叉树 (Full Binary Tree)
  1. 如果二叉树中所有分支结点的度数都为 2，且叶子结点都在同一层次上，则称这类二叉树为满叉树。
• 完全二叉树 (Complete Binary Tree)
  1. 如果一棵具有 n 个结点的高度为 k 的二叉树，它的每一个结点都与高度为 k 的满二叉树中编号为 1 — n 的结点一一对应，则称这棵二叉树为完全二叉树。( 从上到下从左到右编号 )

完全二叉树的特性：

• 同样结点数的二叉树，完全二叉树的高度最小
• 完全二叉树的叶结点仅出现在最下面两层
  1. 最底层的叶结点一定出现在左边
  2. 倒数第二层的叶结点一定出现在右边
  3. 完全二叉树中度为 1 的结点只有左孩子

2.二叉树的深层特性

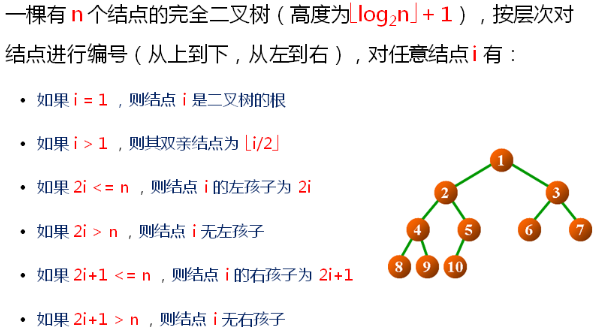
性质1：

性质2：

性质3：

性质4：

性质5（这一条性质为完全二叉树所特有，普通二叉树不具备。）：

3.二叉树的存储结构设计

本节目标：

• 完成二叉树和二叉树结点的存储结构设计

设计要点：

• BTree 为二叉树结构，每个结点最多只有两个后继结点
• BTreeNode 只包含 4 个固定的公有成员 ( 哪4个？ )
• 实现树结构的所有操作 ( 增，删，查，等 )

BTreeNode 的设计与实现：

BTree 的设计与实现：

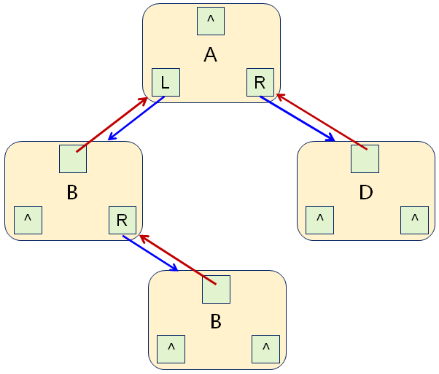
BTree ( 二叉树结构 ) 的实现架构：

重构父类TreeNode类和Tree类：
TreeNode.h

#ifndef TREENODE_H
#define TREENODE_H

#include "Object.h"

namespace StLib
{

template <typename T>
class TreeNode : public Object
{
protected:
    bool m_flag;

    TreeNode(const TreeNode<T>&);
    TreeNode<T>& operator = (const TreeNode<T>&);

    void* operator new(size_t size) throw()
    {
        return Object::operator new(size);
    }
public:
    T value;
    TreeNode<T>* parent;

    TreeNode()
    {
        m_flag = false;
        parent = NULL;
    }

    bool flag()
    {
        return m_flag;
    }

    virtual ~TreeNode() = 0;
};

template <typename T>
TreeNode<T>::~TreeNode()
{

}

}

#endif // TREENODE_H

Tree.h

#ifndef TREE_H
#define TREE_H

#include "TreeNode.h"
#include "SharedPointer.h"

namespace StLib
{

template <typename T>
class Tree : public Object
{
protected:
    TreeNode<T>* m_root;

    Tree(const Tree<T>&);
    Tree<T>& operator = (const Tree<T>&);
public:
    Tree() { m_root = NULL; }
    virtual bool insert(TreeNode<T>* node) = 0;
    virtual bool insert(const T& value, TreeNode<T>* parent) = 0;
    virtual SharedPointer< Tree<T> > remove(const T& value) = 0;
    virtual SharedPointer< Tree<T> > remove(TreeNode<T>* node) = 0;
    virtual TreeNode<T>* find(const T& value) const = 0;
    virtual TreeNode<T>* find(TreeNode<T>* node) const = 0;
    virtual TreeNode<T>* root() const = 0;
    virtual int degree() const = 0;
    virtual int count() const = 0;
    virtual int height() const = 0;
    virtual void clear() = 0;
};

}

#endif // TREE_H

修改对应的GTreeNode类：
GTreeNode.h

#ifndef GTREENODE_H
#define GTREENODE_H

#include "TreeNode.h"
#include "LinkList.h"

namespace StLib
{

template <typename T>
class GTreeNode : public TreeNode<T>
{
public:
    LinkList<GTreeNode<T>*> child;

    static GTreeNode<T>* NewNode()
    {
        GTreeNode<T>* ret = new GTreeNode<T>();

        if( ret != NULL )
        {
            ret->m_flag = true;
        }

        return ret;
    }
};

}

#endif // GTREENODE_H

在StLib中定义BTreeNode类和BTree类：
BTreeNode.h

#ifndef BTREENODE_H
#define BTREENODE_H

#include "TreeNode.h"

namespace StLib
{

template <typename T>
class BTreeNode : public TreeNode<T>
{
public:
    BTreeNode<T>* left;
    BTreeNode<T>* right;

    BTreeNode()
    {
        left = NULL;
        right = NULL;
    }

    static BTreeNode<T>* NewNode()
    {
        BTreeNode<T>* ret = new BTreeNode<T>();

        if( ret != NULL )
        {
            ret->m_flag = true;
        }

        return ret;
    }
};

}

#endif // BTREENODE_H

BTree.h

#ifndef BTREE_H
#define BTREE_H

#include "Tree.h"
#include "BTreeNode.h"
#include "Exception.h"
#include "LinkQueue.h"

namespace StLib
{

template <typename T>
class BTree : public Tree<T>
{
public:
    bool insert(TreeNode<T>* node)
    {
        bool ret = true;

        return ret;
    }

    bool insert(const T& value, TreeNode<T>* parent)
    {
        bool ret = true;

        return ret;
    }

    SharedPointer< Tree<T> > remove(const T& value)
    {
        return NULL;
    }

    SharedPointer< Tree<T> > remove(TreeNode<T>* node)
    {
        return NULL;
    }

    BTreeNode<T>* find(const T& value) const
    {
        return NULL;
    }

    BTreeNode<T>* find(TreeNode<T>* node) const
    {
        return NULL;
    }

    BTreeNode<T>* root() const
    {
        return dynamic_cast<BTreeNode<T>*>(this->m_root);
    }

    int degree() const
    {
        return NULL;
    }

    int count() const
    {
        return NULL;
    }

    int height() const
    {
        return NULL;
    }

    void clear()
    {
        this->m_root = NULL;
    }

    ~BTree()
    {
        clear();
    }
};

}

#endif // BTREE_H

4.小结

• 通用树结构采用了双亲结点表示法进行描述
• 孩子兄弟表示法有能力描述任意类型的树结构
• 孩子兄弟表示法能够将通用树转化为二叉树
• 二叉树是最多只有两个孩子的树