解法一 袖珍计算器法
思路:将开方运算转化为其他函数运算
注意点:由于对数与指数运算都是浮点型运算,因此存在精度缺失的问题,因此在得到结果的整数部分 ans 后,我们应当找出 ans 与 ans+1 中哪一个是真正的答案。
class Solution {
/**
*袖珍计算器法,使用对数、指数运算代替开方运算,时间复杂度O(1),空间复杂度O(1)
*/
public int mySqrt(int x) {
if(x == 0) return 0;//对数真数不能为0
int ans = (int)Math.exp(0.5 * Math.log(x));
//注意浮点运算会出现精度缺失,转化为整数时会出现“少1”的情况,因此要做判断
return (long)(ans+1)*(ans+1) <= x ? ans+1 : ans;
}
}
解法二 二分查找法
思路:假设x开方后其整数部分为a,则a^2 <= x,并且a是最大的那个整数,因此可以使用二分查找算法,下届设为0,上界设为x,通过比较 m i d 2 mid^2 mid2与x的大小来缩小上下界范围。
class Solution {
/**
*假设x开方后其整数部分为a,则a^2 <= x,因此可以使用二分查找算法
*/
public int mySqrt(int x) {
int lo = 0, hi = x, ans = -1;
while(lo <= hi) {
int mid =lo + (hi - lo)/2;
if((long)mid * mid <= x){
ans = mid;//更新结果
lo = mid + 1;
}else {
hi = mid - 1;
}
}
return ans;
}
}
解法三 牛顿迭代法
要求x的开方则就是求
f
(
t
)
=
t
2
−
x
f(t)=t^2 - x
f(t)=t2−x的正根,可以将f(t)在某个初始值进行泰勒展开,取前两项作为近似函数
g
(
t
)
g(t)
g(t)近似
f
(
t
)
f(t)
f(t),由近似函数
g
(
t
)
g(t)
g(t)计算得到的根作为初始值再次近似
f
(
x
)
f(x)
f(x)这样近似函数的根就会越来越接近真实值,我们只需要设置一个可以接受的偏差e,当近似值小于这个偏差时就得到了结果。
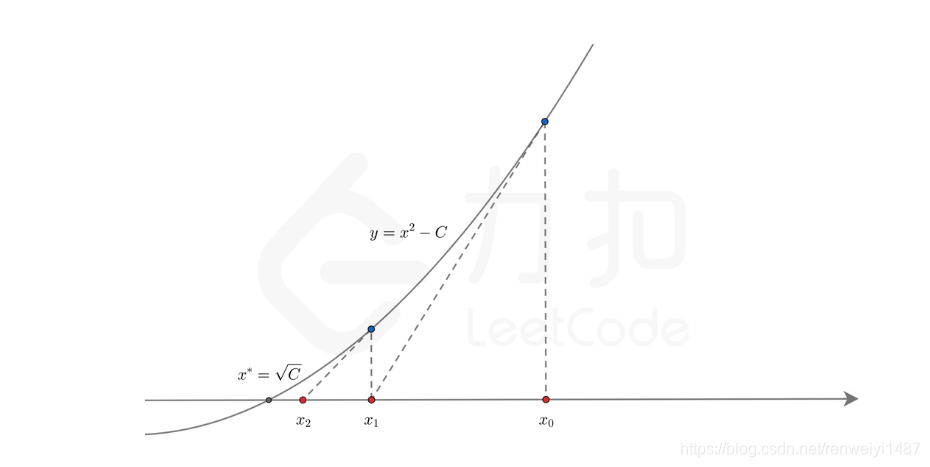
这篇文章讲的很清楚:传送门
class Solution {
public int mySqrt(int x) {
if(x=0)return 0;
double c = (double)x;
double e = 1e-15;
double t = c;//设置初始值
while(Math.abs(t - c/t)> e * t)
t = (t + c/t)/2;
return (int)t;
}
}