线性表之顺序表的操作

数据结构：首先放图一张，明确线性表，顺序存储，链式存储等之间的联系。

1：线性表

1.1线性表的实现方法----数组

2个常用操作：插入、删除

 1）： bool insert(const Elem&);

 2）： bool remove(Elem&);             

详解：

 1）： bool insert(const Elem&); //顺序表结点插入操作----------往后移动一位

template <class Elem>

  bool Alist<Elem>::insert(const Elem& item)

  {  if (listSize==maxSize) return false;//边界检查

     for (int i=listSize;i>fence;i--)    //移位图

       listArray[i]=listArray[i-1];    //移位图(a)到图(b)元素的下标加1

      listArray[fence]=item;  //线性表由2个分离部分(partiton)组成，它们被“栅栏”fence分开，其中fence和当前位置对应。

      listSize++; 

      return true;
 }

 2）： bool remove(Elem&);  //删除操作

template <class Elem>
  bool Alist<Elem>::remove(Elem& it) 
  {  if (rightLength()==0) return false;//边界检查
     it=listArray[fence];
     for (int i=fence;i<listSize-1;i++)    //移位
       listArray[i]=listArray[i+1];
     listSize--;                      //listSize少1
     return true;
   }
      

1.2线性表的实现方法----链表

2个常用的操作：插入、删除

1.2.1：单链表

1）单链表节点的插入：

template <class Elem>
bool LList<Elem>::insert(const Elem& item) {
  fence->next=new link<Elem>(item, fence->next);
  if (tail == fence) tail =fence->next;
  rightcnt++;
  return true;
}  
创建新的结点并且赋给新值。
  –new link<Elem>(item, fence->next);
当前结点元素前驱的next 域要指向新插入的结点。
  –fence->next=new link<Elem>(item, fence->next);

2）单链表节点的删除

template <class Elem>
bool LList<Elem>::remove(Elem& it) {
  if (fence->next==NULL) return false;
  it =fence->next->element;
  link<Elem>* ltemp =fence->next;
  fence->next =ltemp->next;
  if (tail == ltemp) tail =fence;
  delete ltemp;
  rightcnt--;
  return true; 
} 

线性表实现方法的比较：

顺序表

  –插入、删除运算时间代价O(n)

  –预先申请固定长度的数组

  –如果整个数组元素很满，则没有结构性存储开销

链表

  –插入、删除运算时间代价O(1)但找第i个元素删除运算时间代价O(n)

  –存储利用指针， 动态地按照需要为表中新的元素分配存储空间

  –每个元素都有结构性存储开销

1.2.2：循环链表

循环链表的操作：

1）插入：

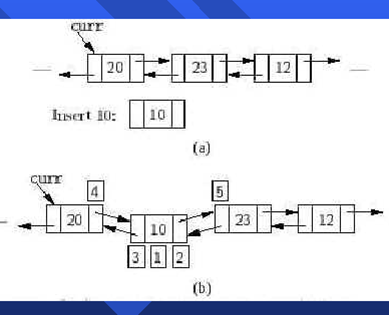
template <class Elem>
bool LList<Elem>::insert(const Elem& item) {
  fence->next=new Link<Elem>(item,fence,fence->next);
  if (fence->next->next!=NULL)
    fence->next->next->prev=fence->next;
  if (tail == fence) tail =fence->next;
  rightcnt++;
  return true;
}  

2）删除：

template <class Elem>
bool LList<Elem>::remove(Elem& it) {
  if (fence->next==NULL) return false;
  it =fence->next->element;
  link<Elem>* ltemp =fence->next;
  if (ltemp->next!=NULL) ltemp->next->prev=fence;
  else tail=fence;
  fence->next =ltemp->next;
  delete ltemp;
  rightcnt--;
  return true; 
} 

2.栈

进栈：

出栈：

 进栈、出栈算法：

void push(const ELEM& item) 
{ if (top==size) return false;
  else { listarray[top++] =item; return true;}
}
bool pop(ELEM& it) {
  if (top==0) return false;
  else {it=listarray[--top];return true;}
}
bool topValue(ELEM& it) const
{ if (top==0) return false;
  else {it=listarray[top-1];return true;}
 }

3.队列

3.1：顺序队列的实现

 bool enqueue(const Elem& it) {
    if (((rear+2)%size)==front) return false;
    rear=(rear+1)%size;
    listArray[rear]=it;
    return true;
  }        
  bool dequeue(Elem& it){
    if (length()==0) return false;
    it=listArray[front];
    front=(front+1)%size;
    return true;
  }

3.2：链式队列的实现

void clear() {            
   while (front != NULL) {         
    rear = front;front = front->next;delete rear; }
   rear = NULL;size=0;
 }
 bool enqueue(const Elem& it) {
   if (rear==NULL) front=rear=new Link<Elem>(it, NULL); 
   else { rear->next = new Link<Elem>(it, NULL);
          rear = rear->next; }
   size++;
   return true;
 }
 bool dequeue(Elem& it) {           
   if (size==0) return false;
   it=front->element;
   Link<Elem> *ltemp=front;
   front = front->next;            
   delete ltemp;                    
   if (front == NULL) rear = NULL;
   size--; 
   return true;                     
  }
 bool frontValue(Elem& it) const {
   if (size==0) return false;
   it=front->element;
   return true;
 }
 virtual int length() const {return size;}
};