最小生成树（Prim和Kruscal）

求最小生成树最基本的两种算法，当然，还有其他算法。

最小生成树

概念

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

概述

在一给定的无向图G = (V, E) 中，(u, v) 代表连接顶点 u 与顶点 v 的边（即），而 w(u, v) 代表此边的权重，若存在 T 为 E 的子集（即）且为无循环图，使得

的 w(T) 最小，则此 T 为 G 的最小生成树。

 

最小生成树其实是最小权重生成树的简称。

性质

最小生成树性质：设G=(V，E）是一个连通网络，U是顶点集V的一个非空真子集。若(u，v）是G中一条“一个端点在U中（例如：u∈U），另一个端点不在U中的边（例如：v∈V-U），且（u，v）具有最小权值，则一定存在G的一棵最小生成树包括此边（u，v）。

 

（以上来自百度百科）

注：一个图中的最小生成树不一定只有一个，若各边权值不等，则最小生成树唯一，若有2条或2条以上的边权值相等，则最小生成树可能不唯一

Prim

和dijkstra类似，采用红白点思想，就是选中一个起始点，标为红点，其他为白点，然后开始循环，找离所有被标记的红点最近的那个点，并将其标为红点，接着用这个点更新剩余的白点到所有的红点的最短距离，

如此循环n次，得到答案。

图解

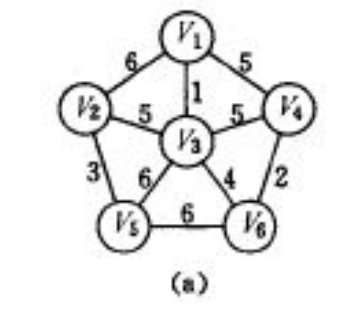
我们选中V1为起始点，并标记为红点，则此时：

dis[V2]=6,dis[V3]=1,dis[V5]=7,dis[V6]=5,dis[V4]=5；

则离红点最近的点是V3，我们选中V3为红点并分别更新其它点到红点的最短距离则此时：

dis[V2]=5,dis[V5]=6,dis[V6]=4,dis[V4]=5；

那么，我们继续循环以上步骤：

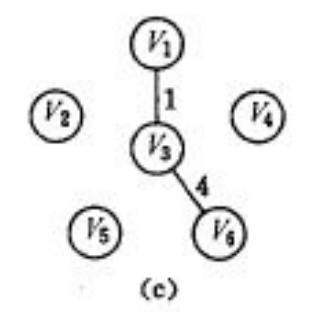
此时离红点最近的点是V6

dis[V2]=5,dis[V5]=6,dis[V4]=2；

此时离红点最近的点是V4

dis[V2]=5,dis[V5]=6；

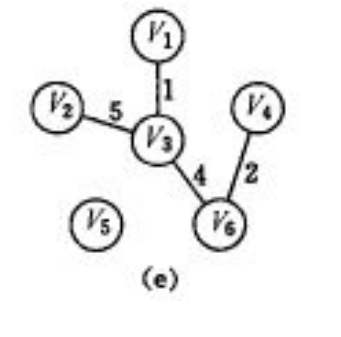
此时离红点最近的点是V2

dis[V5]=6；

完成！！！

代码（普通）

#include<bits/stdc++.h>
using namespace std;
int f[100][100],mt,ft[100],dis[100],n,m;
void input()
{
    int u,v,w;
    cin>>n>>m;
    memset(f,0x7f,sizeof(f));
    memset(ft,0,sizeof(ft));
    memset(dis,0x7f,sizeof(dis));
    ft[1]=true;
    dis[1]=0;
    for(int i=1;i<=m;i++)
    {
        cin>>u>>v>>w;
        f[i][i]=0;
        f[u][v]=f[v][u]=w;
    }
    for(int i=1;i<=n;i++)
    dis[i]=min(dis[i],f[1][i]);
}
void prim()
{
    int k,minn; 
    for(int i=1;i<=n;i++)
    {
        k=0;minn=1e9;
        for(int i=1;i<=n;i++)
        {
            if(!ft[i]&&dis[i]<minn)
            {
                k=i;
                minn=dis[i];
            }
        }
        ft[k]=true;
        if(k==0) break;
        mt=mt+dis[k];
        for(int i=1;i<=n;i++)
        if(!ft[i])
        dis[i]=min(dis[i],f[i][k]);
    }
}
void output()
{
    cout<<mt;
} 
void text1()
{
    input();
    prim();
    output();
}
int main()
{
    text1();
    return 0;
}

代码（堆优化）

堆优化类似dijkstra的堆优化，详情见dijkstra

Kruscal

这个思路很简单，从最小的边开始从小到大枚举，若此边所连的两点至少一点还没有被标记，那么，将此边加入最小生成树并标记点。

#include<bits/stdc++.h>
using namespace std;
int father[100],n,m,k,mt;
struct ed
{
    int from;
    int to;
    int w;
}edge[100];
bool cmp(ed a,ed b)
{
    if(a.w!=b.w)
    return a.w<b.w;
}
int fat(int x)
{
    if(father[x]!=x) father[x]=fat(father[x]);
    return father[x];
}
void unionn(int a,int b)
{
    int fa,fb;
    fa=fat(a);
    fb=fat(b);
    if(fa!=fb) father[fa]=fb;
}
void input()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    father[i]=i;
    for(int i=1;i<=m;i++)
    cin>>edge[i].from>>edge[i].to>>edge[i].w;
    sort(edge+1,edge+m+1,cmp);
}
void kruscal()
{
    for(int i=1;i<=m;i++)
    {
        if(fat(edge[i].from)!=fat(edge[i].to))
        {
            k++;
            mt+=edge[i].w;
            unionn(edge[i].from,edge[i].to);
        }
        if(k==n-1) break;
    }
}
void output()
{
    cout<<mt;
}
void text1()
{
    input();
    kruscal();
    output();
}
int main()
{
    text1();
    return 0;
}

后记：nothing