笔记 | 第一个量子算法：Deutsch-Jozsa算法，非常好懂！

《关于胡小兔的博客又诈尸了这件事》

信息物理真是难啊！上节课讲了量子计算的最基础的概念和Deutsch-Jozsa算法，我看了好几天才看懂……
等考完试估计我就忘了，所以今天先写个博客给未来的我讲讲！

前置技能

// 这部分暂时鸽了。
// 信女愿在博客更新量子计算基础合集，只求小学期两门A-……
// 不过安利一个网站：IBM的量子计算教程，还可以用IBM的qiskit库实践！而且这个网站的颜值真的很高2333

Deutsch算法

众所周知，量子计算机可以利用量子比特（qubit）的叠加态，实现并行计算，从而快速计算一些传统计算机上复杂度很高的问题。但是这种并行计算是怎么实现的呢……？为了理解量子并行，我们找到了一个很好的例子——Deutsch算法。顾名思义，学会这个Deutsch算法，你的Deutsch-Jozsa就学会一大半了（雾

目标

有一个未知的黑盒(f: {0, 1} ightarrow {0, 1})，求(f(0) oplus f(1))（(oplus)表示异或）。

传统算法

在传统计算机上，我们必须调用(f)函数两次，一次求(f(0))，一次求(f(1))，再异或起来，得到答案。但是在量子电路中，只需要一次计算！

量子算法

Deutsch算法就是如下的电路：

其中，中间那个大方块(U_f)是一个特殊的门，输入(x)和(y)，输出(x)和(yoplus f(x))。三个(H)门是Hadamard门，要记得：

[H|0 angle = |+ angle = (|0 angle + |1 angle)/sqrt2 ]

[H|1 angle = |- angle = (|0 angle - |1 angle)/sqrt2 ]

[H|+ angle = |0 angle ]

[H|- angle = |1 angle ]

电路的输入是固定的：(H|psi_0 angle = |01 angle)。接下来，我们来算一下(|psi_1 angle, |psi_2 angle, |psi_3 angle)都是什么，然后就知道测量结果和(f)的关系了！

刚刚说过，(H|0 angle = |+ angle = (|0 angle + |1 angle)/sqrt2, H|1 angle = |- angle = (|0 angle - |1 angle)/sqrt2)，所以

[|psi_1 angle = (H|0 angle)(H|1 angle) = (|0 angle + |1 angle)(|0 angle - |1 angle)/2. ]

接下来就要考虑这个(U_f)了。为了计算方便，我们先设它第一个输入值是(|x angle)，第二个输入值直接代入((|0 angle - |1 angle)/sqrt2)。那么，

[egin{aligned} U_f |x angle (|0 angle - |1 angle)/sqrt2 &= |x angle (|f(x) angle - |1oplus f(x) angle)/sqrt2 \ &= egin{cases} |x angle (|0 angle - |1 angle)/sqrt2, ext{ if }f(x) = 0, \ |x angle (|1 angle - |0 angle)/sqrt2, ext{ if }f(x) = 1 \ end{cases}\ &= (-1)^{f(x)} |x angle (|0 angle - |1 angle)/sqrt2. end{aligned}]

看起来非常的简洁！

接下来把(x = (|0 angle + |1 angle) / sqrt2)代进去：

[egin{aligned} |psi_2 angle &= U_f (|0 angle + |1 angle)(|0 angle - |1 angle)/2 \ &= left[(-1)^{f(0)} |0 angle + (-1)^{f(1)} |1 angle ight] (|0 angle - |1 angle)/2 \ &= (-1)^{f(0)} left[|0 angle + (-1)^{f(0)oplus f(1)} |1 angle ight] (|0 angle - |1 angle)/2. \ end{aligned}]

其实分开写就是

[ |psi_2 angle = egin{cases} (-1)^{f(0)}|+ angle|- angle, ext{ if }f(0) oplus f(1) = 0, \ (-1)^{f(0)}|- angle|- angle, ext{ if }f(0) oplus f(1) = 1. \ end{cases}]

但是我们实在不喜欢(|+ angle)和(|- angle)，还是更喜欢(|0 angle)和(|1 angle)。于是我们又在第一条输出线路上加了一个H门，把(|+ angle)和(|- angle)转换回(|0 angle)和(|1 angle)。这样，(|psi_{3L} angle)（就是(|psi_3 angle)中的第一个qubit，即右上角被测量的那个比特）就是：

[ |psi_{3L} angle = egin{cases} (-1)^{f(0)}|0 angle, ext{ if }f(0) oplus f(1) = 0, \ (-1)^{f(0)}|1 angle, ext{ if }f(0) oplus f(1) = 1. \ end{cases}]

这样我们只需要沿(|0 angle)测量一下(|psi_{3L} angle)，测出(|0 angle)就说明(f(0) oplus f(1) = 0)，反之就说明(f(0) oplus f(1) = 1)，这样就可以100%确定(f(0) oplus f(1))的值了！至此就是Deutsch算法的内容。

神奇的地方在于：在量子版的算法中，我们只调用了一次(U_f)！而在传统计算机上，我们至少要调用两次(f)。你可能会说：差个常数2有啥大不了的嘛！确实，在Deutsch算法并没有在复杂度上体现出量子算法的优越性，但是接下来的Deutsch-Jozsa算法就能体现出本质上的差异了！

Deutsch-Jozsa算法

目标

有一个未知的黑盒(f: {0, 1}^n ightarrow {0, 1})，(f)可能有以下两种性质之一：

• f是常函数。
• f是均匀的（balanced）。这里均匀指的是：(f(x))对于恰好一半的(x)得(0)，而对另恰好一半的(x)得(1)。

求(f)具有以上两种性质中的哪一种。

量子算法

Deutsch-Jozsa算法的电路图：

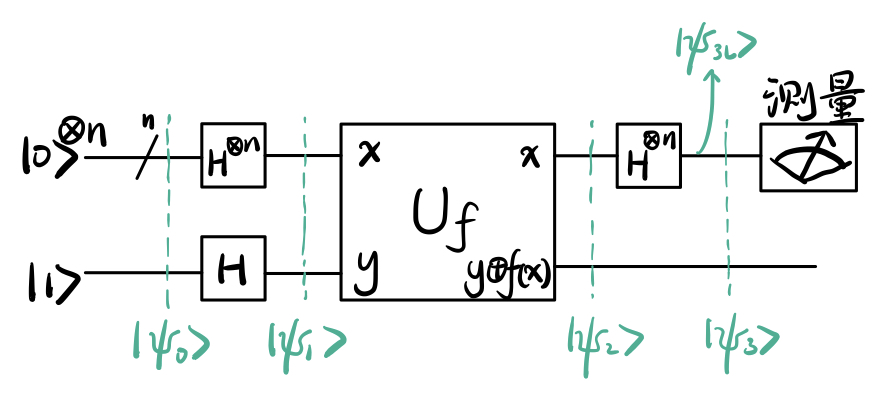
上面那“一条”线路实际上是(n)条，左上角的( ot-^n)符号表示这条线路代表(n)条线路。输入也随之变成了(|psi_0 angle = |0 angle^{otimes n}|1 angle)。可以发现，Deutsch-Jozsa算法的电路图除了把第一条线路扩成了(n)条之外，和Deutsch算法的电路图并没有什么区别。（是不是突然有自信看懂了！）

让我们再用熟悉的方法，逐个计算(|psi_0 angle, |psi_1 angle, |psi_2 angle, |psi_3 angle)。

[egin{aligned} |psi_1 angle &= (H|0 angle^{otimes n})(H|1 angle) \ &= frac{1}{sqrt2^n}(|0 angle + |1 angle)otimes(|0 angle + |1 angle)otimescdotsotimes(|0 angle + |1 angle)otimes(|0 angle - |1 angle)/sqrt2\ &= frac{1}{sqrt2^n} sum_{xin {0, 1}^n} |x angle (|0 angle - |1 angle) / sqrt2.\ |psi_2 angle &= U_f |psi_1 angle = frac{1}{sqrt2^n} sum_{xin {0, 1}^n} (-1)^{f(x)} |x angle (|0 angle - |1 angle) / sqrt2. end{aligned}]

最后一步，我们要计算(|psi_{3L} angle = H|psi_2 angle)。这一步稍微有点难算，再坚持一下！

考虑单个qubit(x_1)，有
(H|x_1 angle = sum_{z_1 in {0, 1}} (-1)^{x_1z_1} |z_1 angle)，
那么对(n)个qubit组成的(|x angle)，有

[H|x angle = H|x_1 x_2 cdots x_n angle = sum_{z in {0, 1}^n} (-1)^{sum_i x_i z_i} |z angle / sqrt2^n. ]

所以

[|psi_{3L} angle = frac{1}{sqrt2^n} sum_{xin {0, 1}^n} (-1)^{f(x)} H|x angle = frac1{2^n} sum_{x in {0, 1}^n} (-1)^{f(x)} sum_{z in {0, 1}^n} (-1)^{sum_i x_i z_i} |z angle. ]

接下来我们测量一下(|psi_{3L} angle)，见证奇迹的时刻到了！

测得(|0 angle^{otimes n})的概率是：

[langle psi_{3L} | 0 angle langle 0 | psi_{3L} angle = left(frac1{2^n} sum_{xin {0, 1}^n} (-1)^{f(x)} ight)^2, ]

因为除了(| 0 angle)以外的(| z angle)都和(| 0 angle)垂直，内积是0，所以其他项都没了，只剩下(| z angle = | 0 angle)的这一项。

当(f)是常函数时，所有((-1)^{f(x)})都相等，(sum_{xin {0, 1}^n} (-1)^{f(x)} = pm 1)，平方之后就等于(1)，所以测出(|0 angle^{otimes n})的概率是1；
当(f)是均匀的函数时，一半((-1)^{f(x)} = 1)，另一半((-1)^{f(x)} = -1)，(sum_{xin {0, 1}^n} (-1)^{f(x)} = 0)，平方之后依然等于(0)，所以测出(|0 angle^{otimes n})的概率是0。

这样，只需运行这个电路一次，就可以100%确定(f)的性质了！

一些常见的困惑

Q：啥是量子计算……啥是qubit……
A：反正大概是OI用不到的东西……Qiskit Textbook欢迎你！（再次免费打广告）

Q：不是啊，你连(f)是啥都不知道，你这个(U_f)咋从(f)构建出来的啊？
A：好问题！答案是，并不知道怎么构建……这个算法应用的场景其实是“给出一个量子黑盒(U_f)”，而不是给出(f)。（如果给出(f)，把(f)读进来、搞出一个真值表的复杂度就有(2^n)了……总之这个算法解决的问题不是这个。）

Q：只看上面那条线路，(U_f)对于(|x angle)不是相当于单位矩阵(I_n)一样，没有产生改变嘛？为啥第一条线路输出的不是(H^{otimes n}I_nH^{otimes n}|0 angle^{otimes n} = |0 angle^{otimes n})呢？
A：好、好问题！问题出在“(U_f)对于(|x angle)相当于单位矩阵(I_n)”这句话上。事实上，(U_f)并不能写作(I_n otimes U_f')的形式，也就是说(U_f)并不能分成两个矩阵分别影响上下两条线路。

Q：我还是不明白。(|x angle)是(|0 angle^{otimes n})经过H门后得到的，再经过一次H门为啥没变回去？？？
A：换种说法，经过(U_f)门之后，上下两条线路（(|x angle)和(|y angle oplus f(x))）发生了纠缠，所以(U_f)门输出的“两条线路”也无法分成“(|x angle otimes (|y angle oplus f(x)))”这样的“张量积”形式，因而不能分开单独考虑了。

Q：所以这个算法有啥用处吗？
A：它的用处大概是……帮你理解量子并行计算，证明量子并行计算与传统计算机相比有优越之处。现在看起来，Deutsch-Jozsa算法解决的问题或许没啥用处，但或许以后类似的方法能解决更重要的问题吧~（现学现卖，并未深入了解 =_=|||）

---

以上就是Deutsch-Jozsa算法的讲解啦，我也刚学，可能有很多错误，欢迎大佬指正！>v<

Acknowledgement：感谢lpy大佬解答我的菜问题ﾍ(;´Д｀ﾍ)