回溯法是一种选优搜索法(试探法),被称为通用的解题方法,这种方法适用于解一些组合数相当大的问题。通过剪枝(约束+限界)可以大幅减少解决问题的计算量(搜索量)。
基本思想
将n元问题P的状态空间E表示成一棵高为n的带权有序树T,把在E中求问题P的解转化为在T中搜索问题P的解。
深度优先搜索(Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。 --from wiki
实现方法
1、按选优条件对T进行深度优先搜索,以达到目标。
2、从根结点出发深度优先搜索解空间树
3、当探索到某一结点时,要先判断该结点是否包含问题的解
- 如果包含,就从该结点出发继续按深度优先策略搜索
- 否则逐层向其祖先结点回溯(退回一步重新选择)
- 满足回溯条件的某个状态的点称为“回溯点”
4、算法结束条件
- 求所有解:回溯到根,且根的所有子树均已搜索完成
- 求任一解:只要搜索到问题的一个解就可以结束
遍历过程
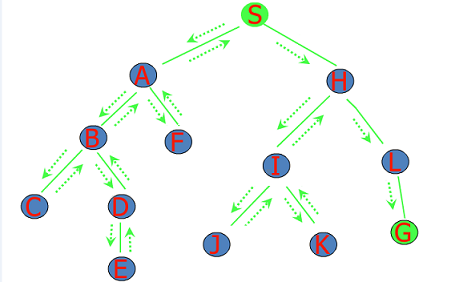
典型的解空间树
第一类解空间树:子集树
当问题是:从n个元素的集合S中找出满足某种性质的子集时相应的解空间树称为子集树,例如n个物品的0/1背包问题。
- 这类子集树通常有2^n个叶结点
- 解空间树的结点总数为2^(n+1) - 1
- 遍历子集树的算法需Ω(2^n)计算时间
第二类解空间树:排列树
当问题是:确定n个元素满足某种性质的排列时相应的解空间树称为排列树,例如旅行商问题。
DFS搜索在程序中可以两种方式来实现,分别是非递归方式和递归方式。前者思路更加清晰,便于理解,后者代码更加简洁高效。
非递归实现
非递归实现需要借助堆栈(先入后出,后入先出),在C++中使用stack容器即可。
问题
若给定一个序列,需要找到其中的一个子序列,判断是否满足一定的条件。下面将程序实现DFS对子序列的搜索过程。
实现步骤:
1、首先将根节点放入堆栈中。
2、从堆栈中取出第一个节点,并检验它是否为目标。
- 如果找到目标,则结束搜寻并回传结果。
- 否则将它某一个尚未检验过的直接子节点加入堆栈中。
3、重复步骤2。
4、如果不存在未检测过的直接子节点。
- 将上一级节点加入堆栈中。
- 重复步骤2。
5、重复步骤4。
6、若堆栈为空,表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
C++代码
/*********************************************************************
*
* Ran Chen <wychencr@163.com>
*
* Back-track algorithm (by DFS)
*
*********************************************************************/
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
class Node
{
public:
int num; // 节点中元素个数
int sum; // 节点中元素和
int rank; // 搜索树的层级
int flag; // 0表示子节点都没访问过,1表示访问过左节点,2表示访问过左右节点
vector <int> path; // 节点元素
Node();
Node(const Node & nd);
};
// 默认构造函数
Node::Node()
{
num = 0;
sum = 0;
rank = 0;
flag = 0;
// path is empty
}
// 复制构造函数
Node::Node(const Node & nd)
{
num = nd.num;
sum = nd.sum;
rank = nd.rank;
flag = nd.flag;
path = nd.path;
}
// -----------------------------------------------------------------
void DFS(const vector <int> & deque)
{
stack <Node *> stk; // 存储节点对应的指针
stack <Node *> pre_stk; // 存储上一级节点(回溯队列)
Node * now = new Node; // 指向当前节点
Node * next = NULL; // 指向下一个节点
Node * previous = NULL; // 指向上一个节点
while (now)
{
if (now->rank < deque.size() && (now->flag == 0))
{
// 左叶子节点,选择当前rank的数字
next = new Node(*now);
next->num++;
next->sum += deque[next->rank];
next->path.push_back(deque[next->rank]);
next->rank++;
next->flag = 0;
stk.push(next); // 将左节点加入堆栈中
now->flag = 1; // 改变标志位
// 将当前节点作为上一级节点存储并删除
previous = new Node(*now);
pre_stk.push(previous);
delete (now);
// 取出堆栈中的待选节点作为当前节点
now = stk.top();
stk.pop();
// 显示搜索路径
for (int i = 0; i < next->path.size(); ++i)
{
cout << " " << next->path[i] << " ";
}
cout << endl;
continue; // DFS每次仅选取一个子节点,再进入下一步循环
}
if (now->rank < deque.size() && (now->flag == 1))
{
// 右节点,不选择当前rank的数字
next = new Node(*now);
next->rank++;
next->flag = 0;
stk.push(next);
now->flag = 2;
// 将当前节点作为上一级节点存储并删除
previous = new Node(*now);
pre_stk.push(previous);
delete (now);
// 取出堆栈中的待选节点作为当前节点
now = stk.top();
stk.pop();
continue;
}
// 回溯结束
if (pre_stk.empty())
{
break;
}
// 没有子节点或者没有未搜索过的子节点时,回退到上一级节点(回溯)
if (now->rank >= deque.size() || now->flag == 2)
{
delete (now);
now = pre_stk.top();
pre_stk.pop();
}
}
}
// -----------------------------------------------------------------
int main()
{
stack <Node*> stk;
vector <int> deque { 2,3,5,7 };
DFS(deque);
cin.get();
return 0;
}
运行结果

程序说明
1、定义了一个Node节点类,表示当前状态下已经搜索到的序列,path记录了这个子序列的值,并且类中添加了num(子序列中元素数目)、sum(子序列元素和)等属性,通过这些属性可以判断是否找到满意解或者用于剪枝。
2、对于原始序列中某个位置的数,其子序列中可以包含这个数,也可以不包含这个数,所以每次有两种选择,即每个节点有两个子节点。
3、flag属性标识了当前节点的子节点遍历情况。若flag=0,表示子节点都没访问过,下一步优先访问左节点,所以将左节点加入堆栈中;flag=1,表示访问过左节点,下一步访问右节点;flag=2,表示访问过左右节点。
4、当没有子节点(now->rank >= deque.size())或者左右节点都访问过时(flag=2),回溯到上一级节点。
5、程序循环中,首先通过now当前节点,找到下一个子节点next,将其加入堆栈中,便于下一步循环。在now节点销毁前,将其存到previous,并加入pre_stk堆栈中。这样在下一轮循环中,previous相对于now就是上一级节点,如果now不能找到其子节点,就要返回上一级,这样previous就可以重新赋给now,达到返回上一级的目的。
6、整个程序的终止条件是pre_stk堆栈为空时截止,说明所有节点都已经遍历过,并且没有再可回溯的节点了。实际运用中,可以通过其他属性(搜索到可行解)来提前终止程序。
递归实现
#include<cstdio>
#include <iostream>
int n, k; __int64 sum = 0;
int a[4] = { 2, 3, 5, 7 }, vis[4] = {0, 0, 0, 0};
void DFS(int i, int cnt, int sm)//i为数组元素下标,sm为cnt个数字的乘积
{
if (cnt == k) // 解中已包含k个数字
{
sum = sum + sm; return;
}
if (i >= n)
return;
if (!vis[i])
{
// 对第i个数字进行访问
vis[i] = 1;
//a[i]被选,优先选择第i个加入到解中,接下来搜索第i+1个数字
DFS(i + 1, cnt + 1, sm*a[i]);
//a[i]不选,不选择第i个,相当于右节点,接下来搜素第i+1个数字
DFS(i + 1, cnt, sm);
vis[i] = 0; // 回溯
}
return;
}
int main(void)
{
n = 4, k = 2;
DFS(0, 0, 1);
printf("%I64d
", sum);
std::system("pause");
return 0;
}
程序说明
1、程序目的:给定n个正整数,求出这n个正整数中所有任选k个相乘后的和,这里的数组a[4]存储原序列,vis[4]作为访问标志,k取2,结果输出为101,对应的序列是{2, 3}{2, 5}{2, 7}{3, 5}{3, 7}{5, 7}。
2、对于元素a[i],每次对应两个选择。若选择将a[i]加入到解中,则解中元素个数+1,乘积结果*a[i],所以下一步更新为DFS(i + 1, cnt + 1, sm*a[i])。若不选择a[i],则解中的元素个数和乘积不变,下一步更新为DFS(i + 1, cnt, sm)。
3、回溯时要将标志位重置。