codeforces399D

 题目大意：ainta刷一面n*n的二维墙。墙一开始可能有一些块被刷了。
他终止刷墙的前提是墙的每一行每一列都至少有一块被刷。
他每一次从n*n的墙随机选择一块，如果这一块没有被刷就刷，刷了就无视，刷墙不计入时间，刷完一块之后要休息一分钟(不管无视了没有都要休息)。
他想求期望终止时间是多少。(中国好队友z55250825友情翻译)

n<=2000,m<=n^2

首先我们压缩一下状态，因为这个状态有很多重复的，我们需要记下的只有有多少行被占领了，所以我们记F[i][j]表示还有i行没有占领，还有j列没有占领从这个状态到终止状态的期望时间。

递推方程也比较容易想，状态[i][j]能够到达的状态是[i][j],[i-1][j],[i][j-1],[i-1][j-1],概率也容易算

F[i][j]=

化简一下就是

F[i][j]=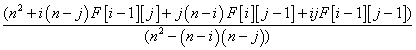

然后注意一下边界情况

#include <cstdio>
using namespace std;

int n,m,l,r;
bool a[2020],b[2020];
double f[2020][2020];

int main() {
    scanf("%d%d",&n,&m);
    l=n;r=n;
    int i,j,x,y;
    for(i=1;i<=m;++i){
        scanf("%d%d",&x,&y);
        if(!a[x])--l;
        if(!b[y])--r;
        a[x]=true;
        b[y]=true;
    }
    for(i=1;i<=l;++i)f[i][0]=(n+i*f[i-1][0])/i;
    for(j=1;j<=r;++j)f[0][j]=(n+j*f[0][j-1])/j;
    for(i=1;i<=l;++i)
    for(j=1;j<=r;++j)
    f[i][j]=(n*n+i*(n-j)*f[i-1][j]+(n-i)*j*f[i][j-1]+i*j*f[i-1][j-1])/(n*n-(n-i)*(n-j));
    printf("%0.8lf
",f[l][r]);
    //printf("%d %d
",l,r);
    return 0;
}