LeetCode-关于二叉搜索树的算法总结

• 二叉搜索树的升序输出或者升序查找第k个元素之类的问题可以依靠中序遍历,BST 相关的问题，要么利用 BST 左小右大的特性提升算法效率，要么利用中序遍历的特性满足题目的要求

• 如果当前节点会对下面的子节点有整体影响，可以通过辅助函数增长参数列表，借助参数传递信息。

• 在二叉树递归框架之上，扩展出一套 BST 代码框架：

  void BST(TreeNode root, int target) {
      if (root.val == target)
       // 找到目标，做点什么
      if (root.val < target)
          BST(root.right, target);
      if (root.val > target)
          BST(root.left, target);
  }
  

• 在此基础上对二叉搜索树进行增删改查以及验证

  验证二叉搜索树的合法性

  在验证是否是二叉搜索树的时候，不应该简单比较左子节点的值<root.val<右节点的值，而是要满足左子树的最大值<root.val< 右子树的最小值，所以要利用辅助函数，增加函数参数列表，在参数中携带额外信息，将这种约束传递给子树的所有节点，限定左子树的最大值是 root.val，右子树的最小值是 root.val，这也是二叉树算法的一个小技巧吧。

  以下是正确代码：

  boolean isValidBST(TreeNode root) {
      return isValidBST(root, null, null);
  }
  
  /* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
  boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
      // base case
      if (root == null) return true;
      // 若 root.val 不符合 max 和 min 的限制，说明不是合法 BST
      if (min != null && root.val <= min.val) return false;
      if (max != null && root.val >= max.val) return false;
      // 限定左子树的最大值是 root.val，右子树的最小值是 root.val
      return isValidBST(root.left, min, root)
              && isValidBST(root.right, root, max);
  }
  

在增删改的时候要结合二叉搜索树的特性，利用二分搜索来减少查找时间，在删的时候要格外注意，

删除二叉搜索树的某个节点

找到目标节点了，比方说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，用图片来说明。

情况 1：A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了。

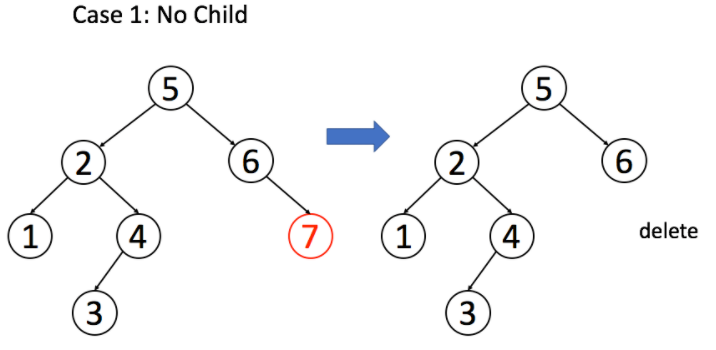
if (root.left == null && root.right == null)
        return null;

情况 2：A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。

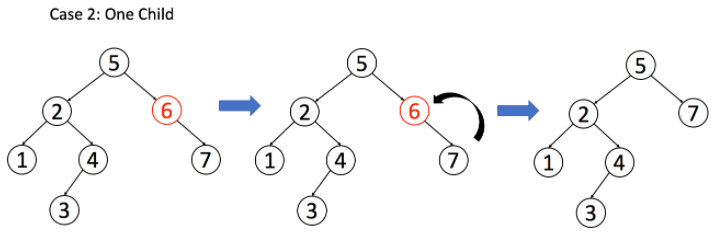
// 排除了情况 1 之后
if (root.left == null) return root.right;
        if (root.right == null) return root.left;

情况 3：A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。

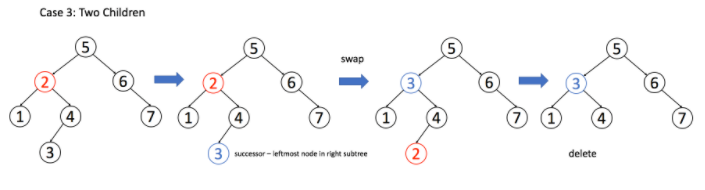
if (root.left != null && root.right != null) {
        // 找到右子树的最小节点
        TreeNode minNode = getMin(root.right);
        // 把 root 改成 minNode
        root.val = minNode.val;
        // 转而去删除 minNode
        root.right = deleteNode(root.right, minNode.val);
 }

三种情况分析完毕，填入框架，简化一下代码：

TreeNode deleteNode(TreeNode root, int key) {
    if (root == null) return null;
    if (root.val == key) {
        // 这两个 if 把情况 1 和 2 都正确处理了
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // 处理情况 3
        TreeNode minNode = getMin(root.right);
        root.val = minNode.val;
        root.right = deleteNode(root.right, minNode.val);
    } else if (root.val > key) {
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        root.right = deleteNode(root.right, key);
    }
    return root;
}

TreeNode getMin(TreeNode node) {
    // BST 最左边的就是最小的
    while (node.left != null) node = node.left;
    return node;
}

不同的二叉搜索树

第 96 题「不同的二叉搜索树」，给你输入一个正整数 n，请你计算，存储 {1,2,3...,n} 这些值共有有多少种不同的 BST 结构。

二叉树算法的关键就在于明确根节点需要做什么，其实 BST 作为一种特殊的二叉树，核心思路也是一样的。

举个例子，比如给算法输入 n = 5，也就是说用 {1,2,3,4,5} 这些数字去构造 BST。

每个数字都可以作为根节点。

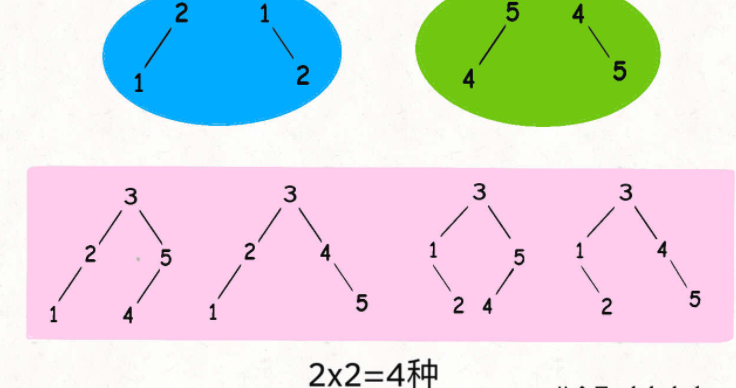
固定 3 作为根节点，这个前提下能有几种不同的 BST 呢？

根据 BST 的特性，根节点的左子树都比根节点的值小，右子树的值都比根节点的值大。

所以如果固定 3 作为根节点，左子树节点就是 {1,2} 的组合，右子树就是 {4,5} 的组合。

左子树的组合数和右子树的组合数乘积就是 3 作为根节点时的 BST 个数。

怎么让算法进行计算呢？

只需要递归就行了，我们可以写这样一个函数：

// 定义：闭区间 [lo, hi] 的数字能组成 count(lo, hi) 种 BST
int count(int lo, int hi);

根据这个函数的定义，结合刚才的分析，可以写出代码：

/* 主函数 */
int numTrees(int n) {
    // 计算闭区间 [1, n] 组成的 BST 个数
    return count(1, n);
}

/* 计算闭区间 [lo, hi] 组成的 BST 个数 */
int count(int lo, int hi) {
    // base case
    if (lo > hi) return 1;
int res = 0;
for (int i = lo; i <= hi; i++) {
    // i 的值作为根节点 root
    int left = count(lo, i - 1);
    int right = count(i + 1, hi);
    // 左右子树的组合数乘积是 BST 的总数
    res += left * right;
}

return res;
}

base case，显然当 lo > hi 闭区间 [lo, hi] 肯定是个空区间，也就对应着空节点 null，虽然是空节点，但是也是一种情况，所以要返回 1 而不能返回 0。

但是时间复杂度非常高，肯定存在重叠子问题。

消除重叠子问题的方法，无非就是加一个备忘录：

// 备忘录
int[][] memo;

int numTrees(int n) {
    // 备忘录的值初始化为 0
    memo = new int[n + 1][n + 1];
    return count(1, n);
}

int count(int lo, int hi) {
    if (lo > hi) return 1;
    // 查备忘录
    if (memo[lo][hi] != 0) {
        return memo[lo][hi];
    }
int res = 0;
for (int mid = lo; mid <= hi; mid++) {
    int left = count(lo, mid - 1);
    int right = count(mid + 1, hi);
    res += left * right;
}
// 将结果存入备忘录
memo[lo][hi] = res;

return res;
}

第 95 题「不同的二叉搜索树 II」，让你构建所有 BST

明白了上道题构造合法 BST 的方法，这道题的思路也是一样的：

1、穷举 root 节点的所有可能。

2、递归构造出左右子树的所有合法 BST。

3、给 root 节点穷举所有左右子树的组合。

代码如下：

/* 主函数 */
public List<TreeNode> generateTrees(int n) {
    if (n == 0) return new LinkedList<>();
    // 构造闭区间 [1, n] 组成的 BST 
    return build(1, n);
}

/* 构造闭区间 [lo, hi] 组成的 BST */
List<TreeNode> build(int lo, int hi) {
    List<TreeNode> res = new LinkedList<>();
    // base case
    if (lo > hi) {
        res.add(null);
        return res;
    }
// 1、穷举 root 节点的所有可能。
for (int i = lo; i <= hi; i++) {
    // 2、递归构造出左右子树的所有合法 BST。
    List<TreeNode> leftTree = build(lo, i - 1);
    List<TreeNode> rightTree = build(i + 1, hi);
    // 3、给 root 节点穷举所有左右子树的组合。
    for (TreeNode left : leftTree) {
        for (TreeNode right : rightTree) {
            // i 作为根节点 root 的值
            TreeNode root = new TreeNode(i);
            root.left = left;
            root.right = right;
            res.add(root);
        }
    }
}

return res;
    
}

总结出了如下几个技巧：

1、如果当前节点会对下面的子节点有整体影响，可以通过辅助函数增长参数列表，借助参数传递信息。

2、在二叉树递归框架之上，扩展出一套 BST 代码框架：

void BST(TreeNode root, int target) {
    if (root.val == target)
    // 找到目标，做点什么
    if (root.val < target)
        BST(root.right, target);
    if (root.val > target)
        BST(root.left, target);
}