第6章讲了图,图还是很好玩的哈,动不动就超时TAT
学习心得:思想很重要啊,代码始终会忘记的,要背的话就背一下基本术语,有统一的定义可以方便和别人沟通
下面分享两道题,一道是拯救007,一道是关于迪杰斯特拉的
1.拯救007

解题思路:1.建图。题目输入只是给了每个点的坐标,我们把它画成图。如果主角能从a点一步跳到b点,我们就把a点和b点用一条线连起来,相当于a和b是连通的。
2.找起点。找主角第一步跳到的点。
3.从起点开始,遍历一遍有该点的连通图,并判断能不能逃出去。(可能有多个起点)
首先想象怎么把数据存起来,我是用结构体数组存坐标,用vector存图(邻接表),用队列存起点
struct node { int x,y;//坐标 bool flag;//到了该点是不是下一跳就能跳出鲨鱼池 }map[maxn]; queue<int> q; vector<int > E[maxn];
然后是输入数据并建图
cin>>n>>m; for(int i=1;i<=n;++i){//输入 cin>>map[i].x>>map[i].y; if(map[i].x>=50-m||map[i].x-m<=-50||map[i].y>=50-m||map[i].y-m<=-50) map[i].flag=1;//下一跳能跳出鲨鱼池,该点flag置1 else map[i].flag=0;//下一跳不能跳出鲨鱼池,该点flag置0 } for(int i=1;i<=n;++i){//n方复杂度建图,如果主角能从i点跳到j点,那么就连一条边 for(int j=1;j<=n;++j){ if((map[i].x-map[j].x)*(map[i].x-map[j].x)+(map[i].y-map[j].y)*(map[i].y-map[j].y)<=m*m) E[i].push_back(j);//邻接表 } if(map[i].x*1.0*map[i].x+map[i].y*map[i].y<=(7.5+m)*(7.5+m)) q.push(i);//找出起点 }
接着,从起点开始进行搜索(我用了dfs搜),我们定义一个全局变量flag,用于判断在搜索过程中是不是逃出去了
dfs:
void dfs(int u) {//从u点开始的dfs if(flag==1) return ;//跳出去了,不跳了不跳了 if(vis[u]) return ;//走过的点不走 vis[u]=1; if(map[u].flag) {//到达安全区的前夕 flag=1;return ; } for(int i=0;i<E[u].size();++i){ int v=E[u][i]; dfs(v); } }
最后,用flag判断主角是不是逃了出去。
AC代码:(大家不要滥用全局变量啊)

/******************补注释************************/ #include<stdio.h> #include<string.h> #include<iostream> #include<algorithm> #include<queue> using namespace std; int n,m,w,flag=0; const int maxn =105; struct node { int x,y;//坐标 bool flag;//到了该点是不是下一跳就能跳出鲨鱼池 }map[maxn]; queue<int> q; vector<int > E[maxn]; bool vis[maxn]; void dfs(int u) { if(flag==1) return ;//跳出去了,不跳了不跳了 if(vis[u]) return ;//走过的点不走 vis[u]=1; if(map[u].flag) {//到达安全区的前夕 flag=1;return ; } for(int i=0;i<E[u].size();++i){ int v=E[u][i]; dfs(v); } } int main() { cin>>n>>m; for(int i=1;i<=n;++i){//输入 cin>>map[i].x>>map[i].y; if(map[i].x>=50-m||map[i].x-m<=-50||map[i].y>=50-m||map[i].y-m<=-50) map[i].flag=1; else map[i].flag=0; } for(int i=1;i<=n;++i){//n方复杂度建图,如果主角能从i点跳到j点,那么就连一条边 for(int j=1;j<=n;++j){ if((map[i].x-map[j].x)*(map[i].x-map[j].x)+(map[i].y-map[j].y)*(map[i].y-map[j].y)<=m*m) E[i].push_back(j); } if(map[i].x*1.0*map[i].x+map[i].y*map[i].y<=(7.5+m)*(7.5+m)) q.push(i);//找出起点 } while(!q.empty()) { int now=q.front(); q.pop(); dfs(now); } if(flag) cout<<"Yes"; else cout<<"No"; return 0; }
/*********************分*********************割*********************线*********************/
第二题:Til the Cows Come Home
题目:http://poj.org/problem?id=2387
题意:给你一幅有n条带权边和m个点的无向图,点的编号是1~n。问从点1到点n的最短距离。
解题思路:迪杰斯特拉裸题
为什么我要把这题放出来呢?其实我只是想分享一下用优先队列优化版的迪杰斯特拉(书本好像没有的哦)
朴素版迪杰斯特拉的时间复杂度是n^2,用优先队列优化后的时间复杂度是nlogn
下面讲思想
假如我有这样一张图,问1到6的最短距离
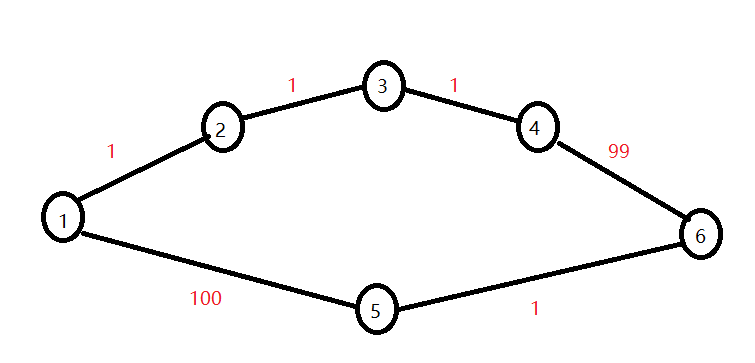
红色数字代表边权(即两点间距离),黑色数字代表节点编号
我们用迪杰斯特拉模拟跑一遍
首先我们开一个数组int d【20】,d【i】代表从起点开始(这里是点1)到 i 点的最短距离
把他们初始化成无穷大,得到数组
d【1】=无穷大,d【2】=无穷大,d【3】=无穷大,d【4】=无穷大,d【5】=无穷大,d【6】=无穷大
然后把起点放入优先队列,更新d【1】=0(自己到自己的距离是0),开始循环,此时数组d:
d【1】=0,d【2】=无穷大,d【3】=无穷大,d【4】=无穷大,d【5】=无穷大,d【6】=无穷大
w(a,b)表示连接点a和点b这条边的权值
优先队列:{1}(我们认为已经知道了队列第一个元素代表的点到起点的最短距离,因为这个是优先队列,按元素对应的d数组值的大小,从小到大的关系排序)
第一轮循环:
把队列的第一个元素拿出来,元素是1
遍历1连着的所有点,发现有2和5
更新d【2】=min(d【2】,d【1】+w(1,2))=min(无穷大,0+1)=1;
更新d【5】=min(d【5】,d【1】+w(1,5))=min(无穷大,0+100)=100;
把2和5放入队列
此时
d【1】=0,d【2】=1,d【3】=无穷大,d【4】=无穷大,d【5】=100,d【6】=无穷大
优先队列:{2,5}(1已经用了,丢掉,2和5的顺序按d【2】=1<d【5】=100这样排)
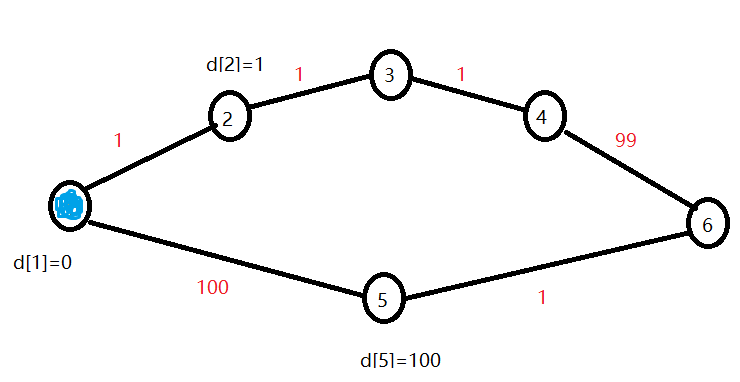
第二轮循环
把队列的第一个元素拿出来,元素是2
遍历2连着的所有点,发现有1和3
发现1已经走过了,不管他
更新d【3】=min(d【3】,d【2】+w(2,3))=min(无穷大,1+1)=2;
把3放入队列
此时
d【1】=0,d【2】=1,d【3】=2,d【4】=无穷大,d【5】=100,d【6】=无穷大
优先队列:{3,5}(d【3】=2 < d【5】=100)

第三轮循环
把队列的第一个元素拿出来,元素是3
遍历3连着的所有点,发现有2和4
发现2已经走过了,不管他
更新d【4】=min(d【4】,d【3】+w(3,4))=min(无穷大,2+1)=3;
把4放入队列
此时
d【1】=0,d【2】=1,d【3】=2,d【4】=3,d【5】=100,d【6】=无穷大
优先队列:{4,5}(d【4】=3 < d【5】=100)
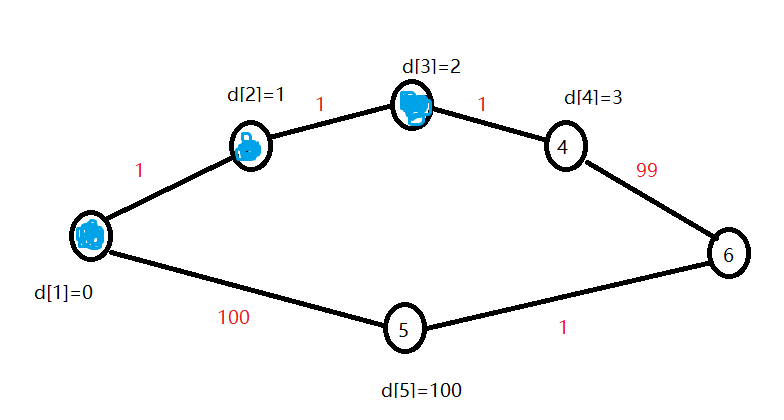
第四轮循环
把队列的第一个元素拿出来,元素是4
遍历4连着的所有点,发现有3和6
发现3已经走过了,不管他
更新d【6】=min(d【6】,d【4】+w(4,6))=min(无穷大,3+99)=102;
把6放入队列
此时
d【1】=0,d【2】=1,d【3】=2,d【4】=3,d【5】=100,d【6】=102
优先队列:{5,6}( d【5】=100 < d【6】=102)

第五轮循环
把队列的第一个元素拿出来,元素是5
遍历5连着的所有点,发现有1和6
发现1已经走过了,不管他
更新d【6】=min(d【6】,d【5】+w(5,6))=min(102,100+1)=101;
把6放入队列
此时
d【1】=0,d【2】=1,d【3】=2,d【4】=3,d【5】=100,d【6】=101
优先队列:{6}

第六轮循环
把队列的第一个元素拿出来,元素是6
遍历6连着的所有点,发现有4和5
发现4和5已经走过了,不管他
d【1】=0,d【2】=1,d【3】=2,d【4】=3,d【5】=100,d【6】=101
优先队列:{}
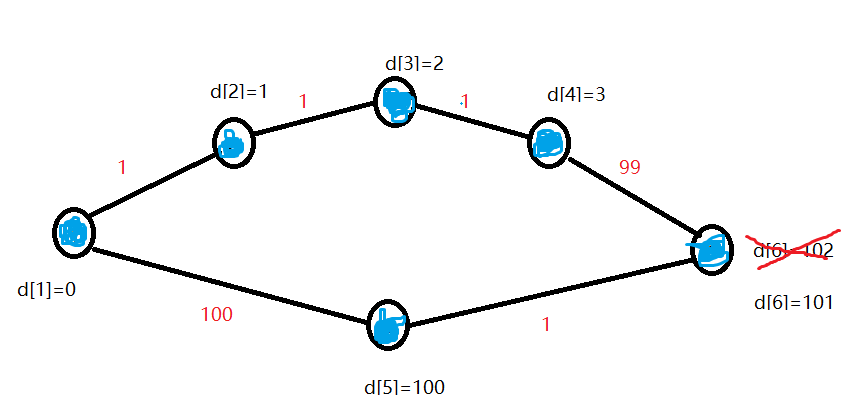
队列为空,d数组全部更新完毕,我们求出起点1到任意一点的最短路径
优化的地方:优先队列可以用logn的时间求出下一个要拿出来的元素时哪一个
代码的话就不说了,慢慢理解,思想最重要
AC代码:

#include <iostream> #include <stdio.h> #include <string.h> #include <queue> using namespace std; const int maxn=1005; vector<pair<int ,int > >E[maxn]; int n,m,d[maxn]; void init() { for(int i=0;i<maxn;i++) E[i].clear(); for(int i=0;i<maxn;i++) d[i]=1e9; } int main() { while(cin>>n>>m) { init(); for(int i=0;i<n;i++) { int x,y,z; scanf("%d%d%d",&x,&y,&z); E[x].push_back(make_pair(y,z)); E[y].push_back(make_pair(x,z)); } int s,t; s=m; t=1; priority_queue< pair<int ,int > >Q; d[s]=0; Q.push(make_pair(-d[s],s)); while(!Q.empty()) { int now=Q.top().second; Q.pop(); for(int i=0;i<E[now].size();i++) { int v=E[now][i].first; if(d[v]>d[now]+E[now][i].second) { d[v]=d[now]+E[now][i].second; Q.push(make_pair(-d[v],v)); } } if(now==t) break; } if(d[t]==1e9) printf("-1 "); else printf("%d ",d[t]); } return 0; }
上次的目标达到了,下次的目标是理解状压DP,好好学习动态规划。
