numpy生成随机数

numpy生成随机数

一、总结

一句话总结：

numpy生成随机数，主要是生成均匀分布和随机分布的随机数

（1）、均匀分布

a、服从[0, 1)之间的均匀分布：
numpy.random.rand(d0, d1, ..., dn)

b、[0, 1)之间均匀抽样：
numpy.random.random(size=None)
和rand函数功能一样，参数不同而已

c、在区间[low, high)中均匀分布：
numpy.random.uniform(low=0.0, high=1.0, size=None)

d、随机整数：在区间[low, high)中离散均匀抽样：
numpy.random.randint(low, high=None, size=None, dtype='l')

（2）、正态分布

a、标准正态分布（均值为0，方差为1）：
numpy.random.randn(d0, d1, ..., dn)

b、服从μ=loc,σ=scale 的正态分布：
numpy.random.normal(loc=0.0, scale=1.0, size=None)
（3）、随机种子

RandomState：定义种子类：RandomState是一个种子类，提供了各种种子方法，最常用seed

seed([seed])：定义全局种子：参数为整数或者矩阵

代码示例：

np.random.seed(1234) #设置随机种子为1234

1、numpy设置随机数种子两种方式？

(甲)、RandomState：定义种子类：RandomState是一个种子类，提供了各种种子方法，最常用seed

(乙)、seed([seed])：定义全局种子：参数为整数或者矩阵

#1为种子，种子不一样，生成的随机数也不一样，但是对每个种子来说，每次运行所生成的随机数是相同的
import numpy as np
rs = np.random.RandomState(1)  
data = rs.rand(30)
print(data)

import numpy as np
np.random.seed(1) #设置随机种子为1
print(np.random.rand(30))

2、电脑产生随机数注意？

（1）、随机数是由随机种子根据一定的计算方法计算出来的数值。所以，只要计算方法一定，随机种子一定，那么产生的随机数就不会变。

（2）、只要用户不设置随机种子，那么在默认情况下随机种子来自系统时钟（即定时/计数器的值）

（3）、随机数产生的算法与系统有关，Windows和Linux是不同的，也就是说，即便是随机种子一样，不同系统产生的随机数也不一样。

二、numpy生成随机数

转自或参考：numpy生成随机数
https://www.cnblogs.com/xk-bench/p/9079533.html

如果你想说，我不想知道里面的逻辑和实现方法，只想要python生成随机数的代码，请移步本文末尾，最简单的demo帮你快速获取实现方法。

先开始背景故事说明：

在数据分析中，数据的获取是第一步，numpy.random 模块提供了非常全的自动产生数据API，是学习数据分析的第一步。 

总体来说，numpy.random模块分为四个部分，对应四种功能： 
1. 简单随机数： 产生简单的随机数据，可以是任何维度 
2. 排列：将所给对象随机排列 
3. 分布：产生指定分布的数据，如高斯分布等 
4. 生成器：种随机数种子，根据同一种子产生的随机数是相同的 
以下是详细内容以及代码实例：（以下代码默认已导入numpy：import numpy as np ）

1. 生成器

电脑产生随机数需要明白以下几点： 
（1）随机数是由随机种子根据一定的计算方法计算出来的数值。所以，只要计算方法一定，随机种子一定，那么产生的随机数就不会变。 
（2）只要用户不设置随机种子，那么在默认情况下随机种子来自系统时钟（即定时/计数器的值） 
（3）随机数产生的算法与系统有关，Windows和Linux是不同的，也就是说，即便是随机种子一样，不同系统产生的随机数也不一样。 
numpy.random 设置种子的方法有：

函数名称	函数功能	参数说明
RandomState	定义种子类	RandomState是一个种子类，提供了各种种子方法，最常用seed
seed([seed])	定义全局种子	参数为整数或者矩阵

代码示例：

np.random.seed(1234) #设置随机种子为1234

2. 简单随机数

函数名称	函数功能	参数说明
rand(d0, d1, …, dn)	产生均匀分布的随机数	dn为第n维数据的维度
randn(d0, d1, …, dn)	产生标准正态分布随机数	dn为第n维数据的维度
randint(low[, high, size, dtype])	产生随机整数	low：最小值；high：最大值；size：数据个数
random_sample([size])	在[0,1）内产生随机数	size：随机数的shape，可以为元祖或者列表，[2,3]表示2维随机数，维度为（2,3）
random([size])	同random_sample([size])	同random_sample([size])
ranf([size])	同random_sample([size])	同random_sample([size])
sample([size]))	同random_sample([size])	同random_sample([size])
choice(a[, size, replace, p])	从a中随机选择指定数据	a：1维数组 size：返回数据形状
bytes(length)	返回随机位	length：位的长度

代码示例

(1) np.random.rand(2,3) #产生2行三列均匀分布随机数组
Out[7]: 
array([[ 0.35369993,  0.0086019 ,  0.52609906],
       [ 0.31978928,  0.27069309,  0.21930115]])

（2）In [8]: np.random.randn(3,3) #三行三列正态分布随机数据
Out[8]: 
array([[ 2.29864491,  0.52591291, -0.80812825],
       [ 0.37035029, -0.07191693, -0.76625886],
       [-1.264493  ,  1.12006474, -0.45698648]])
（3）In [9]: np.random.randint(1,100,[5,5]) #(1,100）以内的5行5列随机整数
Out[9]: 
array([[87, 69,  3, 86, 85],
       [13, 49, 59,  7, 31],
       [19, 96, 70, 10, 71],
       [91, 10, 52, 38, 49],
       [ 8, 21, 55, 96, 34]])
（4）In [10]: np.random.random(10) #(0,1）以内10个随机浮点数
Out[10]: 
array([ 0.33846136,  0.06517708,  0.41138166,  0.34638839,  0.41977818,
        0.37188863,  0.2508949 ,  0.89923638,  0.51341298,  0.71233872])
（5）In [11]: np.random.choice(10) #[0,10)内随机选择一个数
Out[11]: 7

3. 分布

numpy.random模块提供了产生各种分布随机数的API：

函数名称	函数功能	参数说明
beta(a, b[, size])	贝塔分布样本，在 [0, 1]内。
binomial(n, p[, size])	二项分布的样本。
chisquare(df[, size])	卡方分布样本。
dirichlet(alpha[, size])	狄利克雷分布样本。
exponential([scale, size])	指数分布
f(dfnum, dfden[, size])	F分布样本。
gamma(shape[, scale, size])	伽马分布
geometric(p[, size])	几何分布
gumbel([loc, scale, size])	耿贝尔分布。
hypergeometric(ngood, nbad, nsample[, size])	超几何分布样本。
laplace([loc, scale, size])	拉普拉斯或双指数分布样本
logistic([loc, scale, size])	Logistic分布样本
lognormal([mean, sigma, size])	对数正态分布
logseries(p[, size])	对数级数分布。
multinomial(n, pvals[, size])	多项分布
multivariate_normal(mean, cov[, size])	多元正态分布。
negative_binomial(n, p[, size])	负二项分布
noncentral_chisquare(df, nonc[, size])	非中心卡方分布
noncentral_f(dfnum, dfden, nonc[, size])	非中心F分布
normal([loc, scale, size])	正态(高斯)分布
pareto(a[, size])	帕累托（Lomax）分布
poisson([lam, size])	泊松分布
power(a[, size])	Draws samples in [0, 1] from a power distribution with positive exponent a - 1.
rayleigh([scale, size])	Rayleigh 分布
standard_cauchy([size])	标准柯西分布
standard_exponential([size])	标准的指数分布
standard_gamma(shape[, size])	标准伽马分布
standard_normal([size])	标准正态分布 (mean=0, stdev=1).
standard_t(df[, size])	Standard Student’s t distribution with df degrees of freedom.
triangular(left, mode, right[, size])	三角形分布
uniform([low, high, size])	均匀分布
vonmises(mu, kappa[, size])	von Mises分布
wald(mean, scale[, size])	瓦尔德（逆高斯）分布
weibull(a[, size])	Weibull 分布
zipf(a[, size])	齐普夫分布

代码示例

(1)正态分布
import numpy as np
import matplotlib.pyplot as plt

mu = 1  #期望为1
sigma = 3  #标准差为3
num = 10000  #个数为10000

rand_data = np.random.normal(mu, sigma, num)
count, bins, ignored = plt.hist(rand_data, 30, normed=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *np.exp( - (bins - mu)**2 / (2 * sigma**2)), linewidth=2, color='r')
plt.show()

得到图像：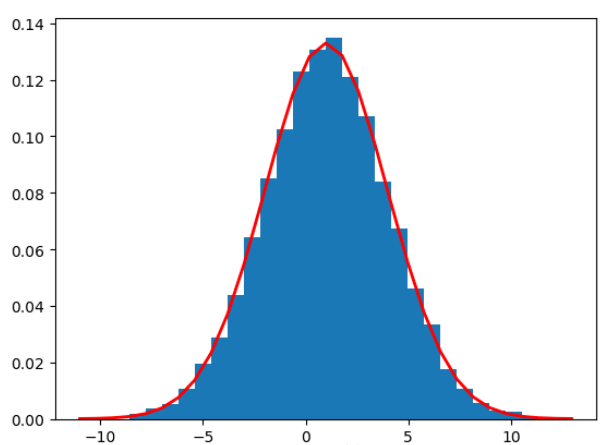 

4. 排列

函数名称	函数功能	参数说明
shuffle(x)	打乱对象x（多维矩阵按照第一维打乱）	矩阵或者列表
permutation(x)	打乱并返回该对象（多维矩阵按照第一维打乱）	整数或者矩阵

代码示例

(1)正态分布
import numpy as np
rand_data = np.random.randint(1, 10, (3, 4))
print(rand_data)
np.random.shuffle(rand_data)
print(rand_data)

out：
[[4 4 4 8]
 [5 6 8 2]
 [1 7 6 6]]
[[4 4 4 8]
 [1 7 6 6]
 [5 6 8 2]]
 （按照行打乱了，也就是交换了行）