机器学习西瓜书笔记---3.2、线性回归
一、总结
一句话总结:
【系统】:系统的学习非常非常重要,所以【看书】是非常非常必要且高效的
1、一元线性回归?
我们先考虑一种最简单的情形:输入【属性的数目只有一个】.为便于讨论,此时我们忽略关于属性的下标,即$$D = { ( x _ { i } , y _ { i } ) } _ { i = 1 } ^ { m }$$
2、离散属性如何转化为连续值?
对离散属性,若属性值间【存在“序”(order)关系】,可通过连续化将其转化为连续值,例如二值属性“身高”的取值“高”“矮”可转化为{1.0,0.0},三值属性“高度”的取值【“高”“中”“低”可转化为{10,0.5,0.0}】;
若属性值间【不存在序关系】,假定有k个属性值,则通常转化为k维向量,例如属性“瓜类”的取值【“西瓜”“南瓜”“黄瓜”可转化为(0,0,1),(0,1,0),(1,0,0)】
若将无序属性连续化,则会【不恰当地引入序关系】,对后续处理如距离计算等造成误导
3、均方误差公式?
【均方误差】是【回归任务中最常用的性能度量】,因此我们可试图让均方误差最小化
$$( w ^ { * } , b ^ { * } ) = underset { ( w , b ) } { arg min } sum _ { i = 1 } ^ { m } ( f ( x _ { i } ) - y _ { i } ) ^ { 2 } = underset { ( w , b ) } { arg min } sum _ { i = 1 } ^ { m } ( y _ { i } - w x _ { i } - b ) ^ { 2 }$$
均方误差有非常好的几何意义,它对应了常用的【欧几里得距离】或简称【“欧氏距离”(Euclidean distance)】.
【基于均方误差最小化】来进行模型求解的方法称为【“最小二乘法”(least square method)】.在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小
4、均方误差和最小二乘法的关系?
【基于均方误差最小化】来进行模型求解的方法称为【“最小二乘法”(least square method)】.在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧氏距离之和最小
5、最小二乘“参数估计”(parameter estimation)?
求解和b使$$E _ { ( w , b ) } = sum _ { i = 1 } ^ { m } ( y _ { i } - w x _ { i } - b ) ^ { 2 }$$【最小化的过程】,称为线性回归模型的最小二乘“参数估计”(parameter estimation).我们可将_$E _ { ( w , b ) }_$分别对w和b求导,得到
【对w求导】:这个公式的推导非常简单,最小二乘法求偏导一步一步即可:$$frac { partial E _ { ( w , b ) } } { partial w } = 2 ( w sum _ { i = 1 } ^ { m } x _ { i } ^ { 2 } - sum _ { i = 1 } ^ { m } ( y _ { i } - b ) x _ { i } )$$:导数为0求得最优解:$$w = frac { sum _ { i = 1 } ^ { m } y _ { i } ( x _ { i } - overline { x } ) } { sum _ { i = 1 } ^ { m } x _ { i } ^ { 2 } - frac { 1 } { m } ( sum _ { i = 1 } ^ { m } x _ { i } ) ^ { 2 } }$$
【对b求导】:这个公式的推导非常简单,最小二乘法求偏导一步一步即可:$$frac { partial E _ { ( w , b ) } } { partial b } = 2 ( m b - sum _ { i = 1 } ^ { m } ( y _ { i } - w x _ { i } ) )$$:导数为0求得最优解:$$b = frac { 1 } { m } sum _ { i = 1 } ^ { m } ( y _ { i } - w x _ { i } )$$
6、“多元线性回归”(multivariate linear regression)?
更一般的情形是如本节开头的数据集D,样本由【d个属性】描述.此时我们试图学得$$f ( x _ { i } ) = w ^ { T } x _ { i } + b , ext { 使得 } f ( x _ { i } ) simeq y _ { i }$$,这称为“多元线性回归”(multivariate linear regression).
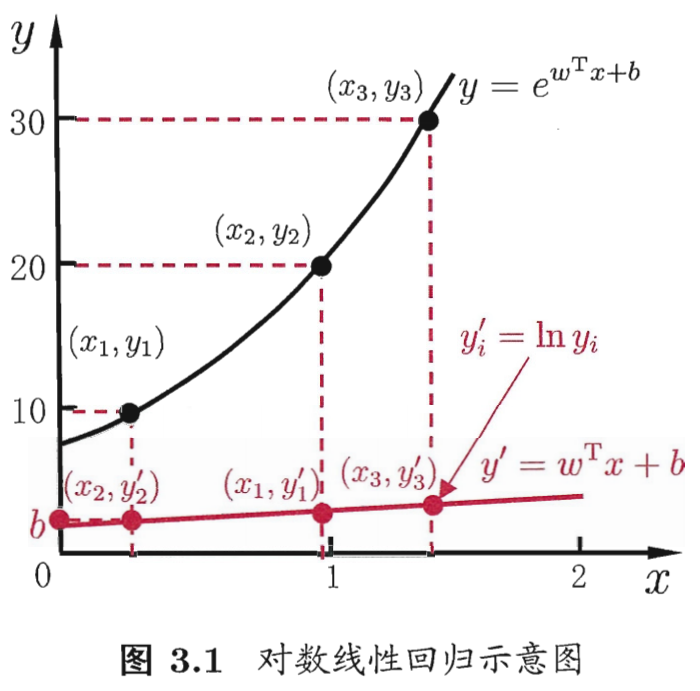
7、“对数线性回归”(log-linear regression)由来?
它实际上是在试图让_$e ^ { w ^ { T } x + b }_$逼近y
我们把线性回归模型简写为:$$y = w ^ { T } x + b$$,可否令模型预测值【逼近y的衍生物】呢?譬如说,假设我们认为示例所对应的输出标记是在指数尺度上变化,那就可将输出标记的对数作为线性模型逼近的目标,即$$ln y = w ^ { T } x + b$$,这就是“对数线性回归”(log-linear regression)
$$ln y = w ^ { T } x + b$$在【形式上仍是线性回归】,但实质上已是在求取输入空间到输出空间的【非线性函数映射】,如图3.1所示.这里的【对数函数】起到了将线性回归模型的预测值与真实标记联系起来的【作用】
8、对数线性回归示意图?
$$y _ { i } ^ { prime } = ln y _ { i }$$
在【形式上仍是线性回归】,但实质上已是在求取输入空间到输出空间的【非线性函数映射】
9、“广义线性模型”(generalized linear model)?
更一般地,考虑单调可微函数g(~),令$$y = g ^ { - 1 } ( w ^ { T } x + b )$$,这样得到的模型称为“广义线性模型”(generalized linear model),其中函数g(~)称为“联系函数”(link function).
显然,【对数线性回归是广义线性模型在g(~)=ln(~)时的特例】
广义线性模型的参数估计常通过【加权最小二乘法】或【极大似然法】进行
二、内容在总结中
博客对应课程的视频位置: