统计学习方法笔记---1202、统计学习方法总结(1.适用问题、2.模型)
一、总结
一句话总结:
【你不懂】:《我在天堂等你》第14集,【社会规则,你不懂,你就算看了再多实例(哪怕是自己经历过的),你还是不懂】。白雪梅和欧战军的年龄差、吸引、事业等。你不懂《大校的女儿》中张雁南说的话,以及韩琳说的话。【你并不真的懂】。
1、监督学习包括哪些方面?
监督学习包括【分类、标注、回归】.
2、分类问题和标注问题的关系?
监督学习包括【分类、标注、回归】.本书主要考虑前两者的学习方法.
分类问题是从实例的特征向量到类标记的预测问题,标注问题是【从观测序列到标记序列】(或状态序列)的预测问题.
可以认为【分类问题是标注问题的特殊情况】.分类问题中可能的预测结果是二类或多类.而标注问题中可能的预测结果是【所有的标记序列】,其数目是指数级的.
3、统计学习方法-这些方法的 【分类、标注、回归】 归类?
感知机、k近邻法、朴素贝叶斯法、决策树是【简单的分类方法】,具有模型直观、方法简单、实现容易等特点.逻辑斯谛回归与最大熵模型、支持向量机、提升方法是【更复杂但更有效的分类方法】,往往分类准确率更高.
原始的感知机、支持向量机以及提升方法是针对【二类分类】的,可以将它们扩展到多类分类.
隐马尔可夫模型、条件随机场是主要的【标注方法】.通常条件随机场的标注准确率更高
EM算法是【含有隐变量】的【概率模型】的一般学习算法,可以用于生成模型的非监督学习
4、统计学习方法-这些方法的 【概率模型与非概率模型】 分类?
朴素贝叶斯法、隐马尔可夫模型是【概率模型】.
感知机、k近邻法、支持向量机、提升方法是【非概率模型】.
而决策树、逻辑斯谛回归与最大熵模型、条件随机场【既可以看作是概率模型,又可以看作是非概率模型】
5、分类问题与函数模型P(Y|X)和Y=f(X)的关系?
分类问题与标注问题的预测模型都可以认为是表示从【输入空间到输出空间的映射】.
它们可以写成【条件概率分布P(Y|X)】或【决策函数Y=f(X)】的形式.
前者表示给定输入条件下输出的【概率模型】,后者表示输入到输出的【非概率模型】.有时,模型更直接地表示为概率模型,或者非概率模型;但有时模型【兼有两种解释】
6、什么是生成方法和判别方法?
【直接学习】条件概率分布P(Y|X)或决策函数Y=f(X)的方法为【判别方法】,对应的模型是【判别模型】。 【感知机、k近邻法、决策树、逻辑斯谛回归与最大熵模型、支持向量机、提升方法、条件随机场】是判别方法.
【首先学习联合概率分布P(X,Y)】,从而【求得条件概率分布P(Y|X)】的方法是【生成方法】,对应的模型是【生成模型】。 【朴素贝叶斯法、隐马尔可夫模型】是生成方法.
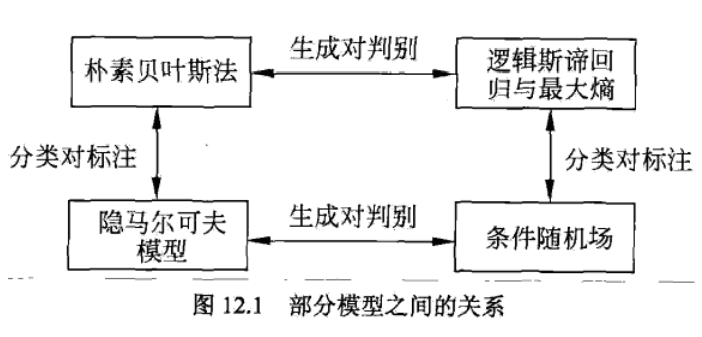
7、朴素贝叶斯法、逻辑斯谛回归与最大熵、隐马尔可夫模型、条件随机场的生成与判别、分类与标注的关系?
朴素贝叶斯法、逻辑斯谛回归与最大熵、隐马尔可夫模型、条件随机场
二、内容在总结中
博客对应课程的视频位置: