算法讲课---2、分治
一、总结
一句话总结:分治在生活中使用的太普遍了,如果在解决生活问题的时候能够想到分治,那绝对会是事半功倍的
1、经典算法-分治的生活中的应用(生活中无处不在的分治)?
管理
a、军队管理(国家管理,企业管理):把部队分为各级组织,将帅就只需要管理少数几个人实现管理全军
b、歌唱选秀(各种选秀):全国分赛区海选,每个赛区的前几名再参加二次海选,最后选择比较优秀的选手参加电视界面比赛
2、分治算法的本质是什么?
子问题
将一个大规模问题分解为若干个规模较小的相同子问题,分而治之。
3、分治法解决问题的条件是什么?
子问题
a、原问题可以分解为若干个规模较小的子问题
b、子问题相互独立
c、子问题的解可以合并为原问题的解
4、分治法的解题步骤?
子问题
a、分解:将原问题分解为规模变小形式相同的子问题。
b、治理:求解各个子问题。
c、合并:将子问题的解逐层合并成原问题的解。
5、分治算法实例?
二分
归并
快排
大整数乘法
a、二分搜索(1-100中猜数)
b、合并排序(归并排序)
c、快排
d、大整数乘法(3278*41926=(32*100+78)*(419*100+26);32*419*10000=(3*10+2)*(41*10+9)*10000)
6、分治算法的事件复杂度?
递推
树
用户递推公式来推一下就出来了
或者把决策树画出来也很明了
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
T(n)= k T(n/m)+f(n)
通过迭代法求得方程的解:
递归方程及其解只给出n等于m的方幂时T(n)的值,但是如果认为T(n)足够平滑,那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升的,从而当mi≤n<mi+1时,T(mi)≤T(n)<T(mi+1)。
7、常用的分治策略?
二分法
等分法
8、分治为什么和递归像是孪生兄弟?
子问题
如果原问题可分割成k个子问题,1<k≤n,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
9、分治法能便利求解的依据是什么?
规模变小 易解
问题的规模越小,越容易直接求解,解题所需的计算时间也越少。例如,对于n个元素的排序问题,当n=1时,不需任何计算。n=2时,只要作一次比较即可排好序。n=3时只要作3次比较即可,…。
10、导入问题国家管理问题的子问题及子问题之间的层次关系是怎样的?
子问题:例如 主席管理国家(省长们)、省长管理省(市长们)、市长管理市(区长们)、区长管理区(村长们)、村长管理村里的那些居民
层次关系:父亲与孩子的关系,祖先与后代的关系
11、分治问题对应的数据结构?
树
12、分治问题对应的算法(子问题规模变小,类型相同)?
递归
13、自顶向下和自底向上是什么?
(自顶向下)a、军队管理(国家管理,企业管理):把部队分为各级组织,将帅就只需要管理少数几个人实现管理全军
(自底向上)b、歌唱选秀(各种选秀):全国分赛区海选,每个赛区的前几名再参加二次海选,最后选择比较优秀的选手参加电视界面比赛
14、自顶向下和自底向上和分治法的解题步骤之间的关系是什么?
(自顶向下)a、分解:将原问题分解为规模变小形式相同的子问题。
b、治理:求解各个子问题。
(自底向上)c、合并:将子问题的解逐层合并成原问题的解。
15、分治法用来解决什么类型的问题?
复杂
分治法就是用来解决复杂问题的
16、分治法反馈到生活的真正核心?
分解 容易解决
把复杂问题分解为容易解决的小问题
17、在子问题形式不同的时候,分治和贪心的关系是什么?
特例
贪心是分治的一种特例啰
二、五大常用算法之一:分治算法
一、基本概念
二、基本思想及策略
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题,1<k≤n,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
三、分治法使用场景
分治法所能解决的问题一般具有以下几个特征:
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解;
4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加;
第二条特征是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用;、
第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
四、分治法得基本步骤
分治法在每一层递归上都有三个步骤:
step1 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
step2 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
step3 合并:将各个子问题的解合并为原问题的解。
它的一般的算法设计模式如下:
Divide-and-Conquer(P)
1. if |P|≤n0
2. then return(ADHOC(P))
3. 将P分解为较小的子问题 P1 ,P2 ,…,Pk
4. for i←1 to k
5. do yi ← Divide-and-Conquer(Pi) △ 递归解决Pi
6. T ← MERGE(y1,y2,…,yk) △ 合并子问题
7. return(T)
其中|P|表示问题P的规模;n0为一阈值,表示当问题P的规模不超过n0时,问题已容易直接解出,不必再继续分解。ADHOC(P)是该分治法中的基本子算法,用于直接解小规模的问题P。因此,当P的规模不超过n0时直接用算法ADHOC(P)求解。算法MERGE(y1,y2,…,yk)是该分治法中的合并子算法,用于将P的子问题P1 ,P2 ,…,Pk的相应的解y1,y2,…,yk合并为P的解。
五、分治法的复杂性分析
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
T(n)= k T(n/m)+f(n)
通过迭代法求得方程的解:
递归方程及其解只给出n等于m的方幂时T(n)的值,但是如果认为T(n)足够平滑,那么由n等于m的方幂时T(n)的值可以估计T(n)的增长速度。通常假定T(n)是单调上升的,从而当mi≤n<mi+1时,T(mi)≤T(n)<T(mi+1)。
六、可使用分治法求解的一些经典问题
七、一些经典问题求解代码实现
1)二分搜索
二分搜索又叫做二分查找、折半查找,它是一种效率较高得查找方法。
二分搜索得要求:
线性表为有序表,并且要用向量作为表得存储结构。
二分搜索得基本思想:先确定待查找记录所在的范围,然后逐步缩小范围直至找到或找不到该记录位置。
二分查找步骤:
1、先确定中间位置:
middle = (left+right)/2;
2、将待查找得key值与data[middle].key值相比较。若相等,则查找成功并返回该位置,否则须确定新得查找区间,继续二分查找,具体方法如下:
- 如果data[middle].key大于key,由于data为有序线性表,可知data[middle...right].key均大于key,因此若表中存在关键字等于key得节点,则一定在位置middle左边的子表中。
- 反之, data[middle].key小于key, 因此若表中存在关键字等于key得节点,则一定在位置middle右边的子表中。下一次查找针对新得区域进行查找。
java代码实现:
1 public static void main(String[] args) { 2 int[] a = {1,2,3,4,5,6,7,8,9}; 3 int pos =bSearch(a, 0, a.length-1, 1); 4 System.out.println(pos); 5 } 6 7 8 public static int bSearch(int[] data,int left,int right,int key){ 9 //获取中间位置 10 int middle = (left+right)/2; 11 //比较key值如相等,返回当前位置,否则确认新的查找空间 12 if(data[middle] == key){ 13 return middle; 14 }else if(data[middle] >key){ 15 return bSearch(data, left, middle-1, key); 16 }else{ 17 return bSearch(data, middle+1, right, key); 18 } 19 }
2)汉诺塔
在汉诺塔游戏中,有三个分别命名为A、B、C得塔座,几个大小各不相同,从小到大一次编号得圆盘,每个原盘中间有一个小孔。最初,所有得圆盘都在A塔座上,其中最大得圆盘在最下面,然后是第二大,以此类推.
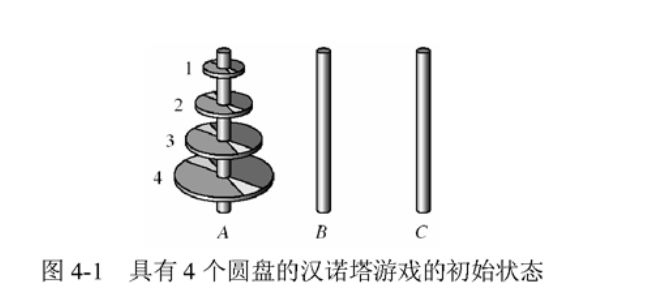
游戏的目的是将所有的圆盘从塔座A移动到塔座B;塔座C用来防止临时圆盘,游戏的规则如下:
1、一次只能移动一个圆盘
2、任何时候都不能将一个较大的圆盘压在较小的圆盘上面.
3、除了第二条限制,任何塔座的最上面的圆盘都可以移动到其他塔座上.
汉诺塔问题解决思想:
在解决汉诺塔问题时,事实上,我们不是罪关心圆盘1开始应该挪到哪个塔座上,而是关心最下面的圆盘4.当然,我们不能直接移动圆盘4,但是圆盘4最终将从塔座A移动到塔座B.按照游戏规则,在移动圆盘4之前的情况一定如下图

我们仍将分析,如何将前三个圆盘从A移动到C,然后圆盘4从A移动到B,前三个圆盘从C再移动到B.
但是上面的步骤可以重复利用!例如将三个圆盘从A移动到C,那么应该先将前两个圆盘从A移动到B,然后将圆盘3从A移动到C,最后将前两个圆盘从B移动到C.
持续简化这个问题,最终我们将只需要处理一个圆盘从一个塔座移动到另一个塔座的问题.
java代码实现:
1 public class Moved { 2 private static int count = 1; 3 public static void main(String[] args) { 4 moved(4, "第一根柱子", "第二根柱子", "第三根柱子"); 5 } 6 7 /** 8 * 9 * @param i 圆盘数量 10 * @param a 圆盘初始所在塔座 11 * @param b 圆盘将要移动到的塔座 12 * @param c 辅助圆盘移动的塔座 13 */ 14 public static void moved(int i,String a,String b,String c){ 15 if(i == 1){ 16 disPaly(1, a, b); 17 }else{ 18 //将i-1根圆盘由A移动到C 19 moved(i-1, a, c, b); 20 //将圆盘i 由A移动到B 21 disPaly(i, a, b); 22 //将i-1根圆盘由C移动到A 23 moved(i-1,c,b,a); 24 } 25 } 26 27 public static void disPaly(int i,String a,String b){ 28 System.out.println("第"+count+"步:移动第"+i+"个塔从"+a+"到"+b); 29 count++; 30 } 31 }
运行结果:
1 第1步:移动第1个塔从第一根柱子到第三根柱子 2 第2步:移动第2个塔从第一根柱子到第二根柱子 3 第3步:移动第1个塔从第三根柱子到第二根柱子 4 第4步:移动第3个塔从第一根柱子到第三根柱子 5 第5步:移动第1个塔从第二根柱子到第一根柱子 6 第6步:移动第2个塔从第二根柱子到第三根柱子 7 第7步:移动第1个塔从第一根柱子到第三根柱子 8 第8步:移动第4个塔从第一根柱子到第二根柱子 9 第9步:移动第1个塔从第三根柱子到第二根柱子 10 第10步:移动第2个塔从第三根柱子到第一根柱子 11 第11步:移动第1个塔从第二根柱子到第一根柱子 12 第12步:移动第3个塔从第三根柱子到第二根柱子 13 第13步:移动第1个塔从第一根柱子到第三根柱子 14 第14步:移动第2个塔从第一根柱子到第二根柱子 15 第15步:移动第1个塔从第三根柱子到第二根柱子
参考:五大常用算法之一:分治算法 - Will_Don - 博客园
https://www.cnblogs.com/xsyfl/p/6921687.html
三、五大算法---分治算法
一:分治算法和递归
1.简述递归
我们要讲到分治算法,我觉得有必要说一下递归,他们就像一对孪生兄弟,经常同时应用在算法设计中,并由此产生许多高效的算法。
直接或间接的调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。
int fibonacci(int n){
if (n <= 1) return 1;
return fibonacci(n-1)+fibonacci(n-2);
}先简单看一下经典的递归例子,博主会找个时间系统详细的总结一下关于递归的内容。
2.简述分治
分治法的设计思想是:
- 分–将问题分解为规模更小的子问题;
- 治–将这些规模更小的子问题逐个击破;
- 合–将已解决的子问题合并,最终得出“母”问题的解;
一个先自顶向下,再自底向上的过程。
凡治众如治寡,分数是也。—孙子兵法
3.分治法与递归的联系
由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。
二:分治法的适用条件
分治法所能解决的问题一般具有以下几个特征:
1) 该问题的规模缩小到一定的程度就可以容易地解决
2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
3) 利用该问题分解出的子问题的解可以合并为该问题的解;
4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。
第一条特征是绝大多数问题都可以满足的,因为问题的复杂性一般是随着问题规模的增加而增加;
第二条特征是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用;、
第三条是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。
第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好
三:分治法的基本步骤
- 分解问题:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;(自顶向下)
这里涉及到一个平衡子问题的思想:人们从大量实践中发现,在用分治法设计算法时,最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡子问题的思想,它几乎总是比子问题规模不等的做法要好。
- 解决问题:如果问题规模较小而容易被解决则直接解,否则递归地解各个子问题,以得到小问题的解。
- 合并结果:将各个子问题的解合并为原问题的解:(自底向上)。
它的一般算法设计模式如下:
divide-and-conquer(P){
if ( | P | <= n0) adhoc(P); //(2)解决问题:递归到小问题,则解决小规模的问题(自顶向下)
divide P into smaller subinstances P1,P2,...,Pk;//(1)分解问题
for (i=1,i<=k,i++)
yi=divide-and-conquer(Pi); //利用递归的解各子问题
return merge(y1,...,yk); //将各子问题的解合并为原问题的解(自底向上)
}四:分治法的复杂性分析
从分治法的一般设计模式可以看出,用他设计出的程序一般是递归算法。因此分治法的计算效率通常可以用递归方程来进行分析。
一个分治法将规模为n的问题分成k个规模为n/m的子问题去解。设分解阀值(表示当问题P规模不超过n0时,问题已容易解出,不必再继续分解)n0=1,且adhoc解规模为1的问题耗费1个单位时间。再设将原问题分解为k个子问题以及用merge将k个子问题的解合并为原问题的解需用f(n)个单位时间。用T(n)表示该分治法解规模为|P|=n的问题所需的计算时间,则有:
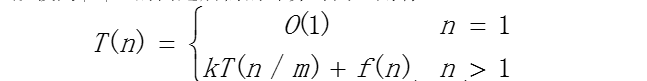
通常可以用展开递归式的方法来解这类递归方程,反复带入求解得
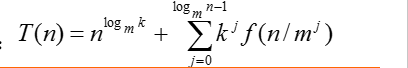
五:分治法的经典例题
- 二分搜索技术
- 大整数的乘法
- Strassen矩阵乘法
- 棋盘覆盖
- 合并排序
- 线性时间选择
- 最接近点对问题
- 快速排序
- 循环日程表
参考资料:
江南大学计算机系袁运浩老师的算法分析课件/计算机算法与分析(第四版)
参考:五大算法---分治算法 - lei_shitou - 博客园
https://www.cnblogs.com/leishitou/p/5436201.html