0x02 基本算法-枚举、模拟、递推

递归实现指数型枚举

int _, n, m, k, x, y;
vector<int> vec;

void calc(int x) {
    if (x == n + 1) {
        for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
        cout << "
";  // 注意一下，以后输出回车用 "
" 而不是 endl
        return;
    }
    calc(x + 1), vec.push_back(x);
    calc(x + 1), vec.pop_back();
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    calc(1);
}

递归实现组合型枚举

int n, m;
vector<int> vec;
void calc(int x) {
    // 剪枝，如果已经选取了超过m个数，
    // 或者即使选上剩下所有数也不够m个就要提前结束搜索了 ↓
    if (vec.size() > m || vec.size() + (n - x + 1) < m) return;
    if (x == n + 1) {
        for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
        cout << "
";  // 注意一下，以后输出回车用 "
" 而不是 endl
        return;
    }
    calc(x + 1), vec.push_back(x);
    calc(x + 1), vec.pop_back();
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    calc(1);
}

递归实现排列型枚举

int n, m;
int order[20];
bool chosen[20];
void cal(int k) {
	if (k == n + 1) {
		for(int i = 1;i<=n;++i)
			cout << order[i] << " ";
		cout << endl; return;
	}
	for (int i = 1;i <= n; ++i) {
		if (chosen[i])continue;
		chosen[i] = true;
		order[k] = i;
		cal(k + 1);
		chosen[i] = false;
	}
}
int main() {
	ios::sync_with_stdio(false), cin.tie(0);
	cin >> n;cal(1);
}

费解的开关

const int N = 6;//因为后续操作读取的是字符串
 
char g[N][N];
char backup[N][N];//备份     --- 用于记录每次枚举第1行的情况
int n;
int dx[5] = {-1,0,1,0,0}, dy[5] = {0,0,0,-1,1};//用于表示当前位置及该位置的上下左右位置的偏移量
 
//改变当前灯及其上下左右灯的状况
void turn(int x, int y){
    for(int i = 0; i < 5; i ++){
        int a = x + dx[i], b = y + dy[i];//用于表示当前位置或该位置的上下左右位置
        if(a >= 0 && a < 5 || b >= 0 && b < 5){
            g[a][b] ^= 1;//用于'0' 和'1'的相互转换     -----根据二者的Ascll码值特点
        }
    }
}
 
int main(){
    cin >> n;
    while(n --){
        for(int i = 0; i < 5; i ++) cin >> g[i];//读取数据
 
        int res = 10;//用于记录操作的结果
        for(int op = 0; op < 32; op ++){//枚举第1行灯的状态 ---- 也可以采用递归实现指数型枚举
            int step = 0;//用于记录当前情况的操作步数
            memcpy(backup, g, sizeof g);//备份原数组数据  ----  因为每次枚举都是一种全新的情况
 
            //枚举第一行，若灯灭，则点亮
            for(int j = 0; j < 5; j ++){
                if(!(op >> j & 1)){//也可以是 if(op >> j & 1) ,因为二者情况数量相同
                    step ++;
                    turn(0, j);//翻转当前灯的状况
                }
            }
 
            //从第一行向下递推至倒数第二行
            for(int i = 0; i < 4; i ++){
                for(int j = 0; j < 5; j ++){
                    if(g[i][j] == '0'){//当前行当前位置灯灭
                        step ++;
                        turn(i + 1, j);//改变当前行的下一行该列灯的状况，使当前行灯亮
                    }
                }
            }
 
            //检验最后一行灯是否全亮,若存在暗灯，则此方案不成立
            bool dark = false;
            for(int j = 0; j < 5; j ++){
                if(g[4][j] == '0'){
                    dark = true;
                    break;
                }
            }
 
            if(!dark) res = min(step, res);
            memcpy(g, backup, sizeof backup);//还原数据,用于下次方案的操作
        }
 
        if(res > 6) res = -1;
        cout << res << endl;
    }
    return 0;
}

// 另一种解
int _, a[6], ans, aa[6];
string s;
void dj(int x, int y) {
    aa[x] ^= (1 << y);
    if (x != 1) aa[x - 1] ^= (1 << y);
    if (x != 5) aa[x + 1] ^= (1 << y);
    if (y != 0) aa[x] ^= (1 << (y - 1));
    if (y != 4) aa[x] ^= (1 << (y + 1));
}
void pd(int p) {
    int k = 0;
    memcpy(aa, a, sizeof(a));
    for (int i = 0; i < 5; ++i)
        if (!((p >> i) & 1)) {
            dj(1, i);
            if (++k >= ans) return;
        }
    for (int x = 1; x < 5; ++x)
        for (int y = 0; y < 5; ++y)
            if (!((aa[x] >> y) & 1)) {
                dj(x + 1, y);
                if (++k >= ans) return;
            }
    if (aa[5] == 31) ans = k;
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    for (cin >> _; _--;) {
        memset(a, 0, sizeof(a));
        for (int i = 1; i <= 5; ++i) {
            cin >> s; // 字符串读入更便利处理
            for (int j = 1; j <= 5; ++j) a[i] = a[i] * 2 + (s[j - 1] - '0');
        }
        ans = 7;
        for (int p = 0; p < (1 << 5); p++) pd(p);
        cout << (ans == 7 ? -1 : ans) << "
";
    }
    return 0;
}

Strange Towers of Hanoi

#define Fi(i, a, b) for (int i = a; i <= b; ++i)
int d[13], f[13];
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    Fi(i, 1, 12) d[i] = d[i - 1] * 2 + 1;
    memset(f, 0x3f, sizeof f), f[1] = 1;
    Fi(i, 2, 12) Fi(j, 1, i) f[i] = min(f[i], 2 * f[j] + d[i - j]);
    Fi(i, 1, 12) cout << f[i] << "
";
    return 0;
}

⭐Sumdiv （AcWing 97. 约数之和）（数论）（分治）

const int p = 9901;
int pow(int x, int y) {
    int ret = 1;
    for (; y; y >>= 1) {
        if (y & 1) ret = 1ll * ret * x % p;
        x = (ll)x * x % p;
    }
    return ret;
}
int main() {
    ios::sync_with_stdio(false), cin.tie(0);
    int a, b, ans = 1;
    cin >> a >> b;
    if (!a) return !puts("0");
    for (int i = 2, num; i * i <= a; i++) {
        num = 0;
        while (a % i == 0) a /= i, num++;
        if (num)
            ans =
                ans * (pow(i, num * b + 1) - 1 + p) % p * pow(i - 1, p - 2) % p;
    }
    if (a > 1) ans = ans * (pow(a, b + 1) - 1 + p) % p * pow(a - 1, p - 2) % p;
    cout << ans << "
";
    return 0;
}

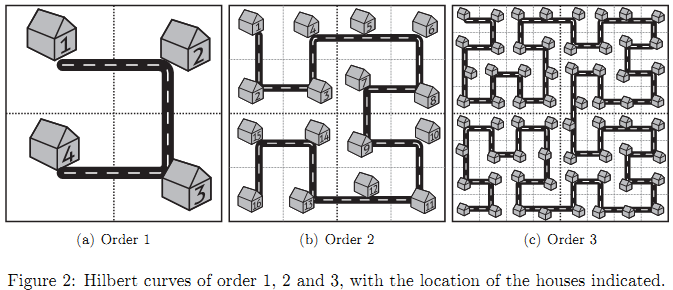
⭐Fractal Streets

题解来源：Click Here

题意：
　　 给你一个原始的分形图,t组数据,对于每组数据,输入3个数n,h,o (n为在第n级,h,o为两个房子的编号),求在第n级情况下,编号为h和o的两个点之间的距离*10为多少。
　　其中,第n级分形图形成规则如下:

1. 首先先在右下角和右上角复制一遍n-1情况下的分形图
2. 然后将n-1情况下的分形图顺时针旋转90度,放到左上角
3. 最后将n-1情况下的分形图逆时针旋转90度 ,放到左下角
   编号是从左上角那个点开始计1,沿着道路计数。

这是著名的通过一定规律无限包含自身的分形图。为了计算方便，我们将题目中房屋编号从0开始编号，那么S与D也都减掉1.
大体思路：设calc(n,m)求编号为m的房屋编号在n级城市中的坐标位置,那么距离是：calc(n,s-1) 与 calc(n,d-1)的距离。
从n(n > 1)级城市由四座n-1级城市组成，其中：
　　1.左上的n-1级城市由城市结构顺时针旋转90度，从编号的顺序看，该结构还做水平翻转，坐标转换至n级时如下图。
　　2与3.右上和右下和原始城市结构一样，坐标转换至n级时如下图。

市由城市结构逆时针旋转90度，从编号的顺序看，该结构也做了水平翻转。
　
　　旋转坐标的变化可通过公式：

　(设len = 2(n-1))当旋转角度是逆时针90度时，也就是顺时针270度时，（x，y）->(y, -x),然后再进行水平翻转，（y,-x）->(-y,-x)。然后再将图形平移到n级图形的左下角，在格子上的坐标变化是，水平方向增加len - 1个位置，垂直方向增加2len - 1个位置。因此坐标（x,y）按照规则转移到了（2len-1-y,len-1-x）.
　　注意：n-1级格子里拥有的房子数量是cnt = 22n /4,即22n-2.
　　　　当前编号m在N级格子的哪个方位是：m / cnt.
　　　　当前编号m在n-1级格子里的编号是: m %cnt;
详细代码如下：

using ll = long long;
pair<ll, ll> calc(ll n, ll m) {
    if (n == 0) return make_pair(0, 0);  //边界
    ll len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    pair<ll, ll> zb = calc(n - 1, m % cnt);
    ll x = zb.first, y = zb.second;
    ll z = m / cnt;
    switch (z) {
        case 0: return make_pair(y, x); break;
        case 1: return make_pair(x, y + len); break;
        case 2: return make_pair(x + len, y + len); break;
        case 3: return make_pair(2 * len - y - 1, len - x - 1); break;
    }
}
int main() {
    int t;
    cin >> t;
    while (t--) {
        ll n, s, d;
        cin >> n >> s >> d;
        pair<ll, ll> zb;
        pair<ll, ll> bz;
        double ans = 0;
        zb = calc(n, s - 1);  //记得-1 QWQ
        bz = calc(n, d - 1);
        ll x, y;
        x = (zb.first - bz.first), y = (zb.second - bz.second);  //边长居然是10
        ans = sqrt(x * x + y * y) * 10;  //喜闻乐见 勾股定理
        printf("%.0f
", ans);           //四舍五入
    }
    return 0;
}

非递归实现组合型枚举

#include <iostream>
#include <vector>
using namespace std;
vector<int> chosen;
int n, m;
void dfs(int x);
int main() {
    cin >> n >> m;
    dfs(1);
}
void dfs(int x) {
    if (chosen.size() > m || chosen.size() + (n - x + 1) < m) return;
    if (x == n + 1) {
        // if(chosen.size() == 0) return;
        for (int i = 0; i < chosen.size(); i++) printf("%d ", chosen[i]);
        puts("");
        return;
    }
    chosen.push_back(x);
    dfs(x + 1);
    chosen.pop_back();
    dfs(x + 1);
    return;
}