《算法竞赛进阶指南》蓝书重做记录

重新复习蓝书（基础算法，数论，DP和图论），争取 (1.5) 个月内完成，期间会不定期更新

此次记录，过往的题也会重新编写题解并收录

补题链接：Here

Initialize02学长的学习笔记

0x00 基本算法

0x01 位运算

A题：a^b

https://ac.nowcoder.com/acm/contest/996/A

题目描述
求 a 的 b 次方对 p 取模的值，其中 0 <= a,b,p <= 10^9

输入描述:
三个用空格隔开的整数a,b和p。

输出描述:
一个整数，表示a^b mod p的值。

实例：
输入： 2 3 9
输出： 8

思路：
这道题是要先算出a的b次幂再对其结果进行求模（取余），因为b最大可为1e+9，按普通做法来做时间复杂度就太大了，显然这样过不了题，
能快速算a的b次幂，就能减小时间复杂度，快速幂就是一种不错的方法。

什么是快速幂：
快速幂是一种简化运算底数的n次幂的算法，理论上其时间复杂度为 O(log₂N)，而一般的朴素算法则需要O(N)的时间复杂度。简单来说快速幂其实就是抽取了指数中的2的n次幂，将其转换为时间复杂度为O(1)的二进制移位运算，所以相应地，时间复杂度降低为O(log₂N)。

代码原理：
以 (a^{13}) 为例，
先把指数13化为二进制就是1101，把二进制数字1101直观地表现为十进制则是如下的等式：

[13 = 1 * (2^3) + 1 * (2^2) + 0 * (2^ 1) + 1 * (2^0) ]

这样一来 (a^{13}) 可以如下算出：

[a^{13} = a ^ {(2^3)} * a ^ {(2^2)} * a ^ {(2^0)} ]

完整AC代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;//将long long类型取个别名：ll类型，为了方便

int power(int a, int b, int mod) {
	ll ans = 1 % mod;
	for (; b; b >>= 1) {
		if (b & 1) ans = ans * a % mod;
		a = (ll)a * a % mod;//显式转化为ll类型进行高精度计算，再隐式转化为int
	}
	return ans;
}

int main() {
	//freopen("in.txt", "r", stdin);
	ios::sync_with_stdio(false), cin.tie(0);
	int a, b, mod;
	cin >> a >> b >> mod;
	cout << power(a, b, mod) << endl;
}

B题：Raising Modulo Numbers

与上面A题写法一样

typedef long long ll;
int _;
// 稍微优化下上方代码：update 21/01/28
ll qpow(ll a, ll b, ll mod) {
    ll ans = 1;
    a %= mod;
    for (; b; a = a * a % mod, b >>= 1)
        if (b & 1) ans = ans * a % mod;
    return ans;
}
int main() {
    // freopen("in.txt", "r", stdin);
    ios_base::sync_with_stdio(false), cin.tie(0);
    ll M, N;
    for (cin >> _; _--;) {
        cin >> M >> N;
        ll a, b, ans = 0;
        while (N--) {
            cin >> a >> b;
            ans = (ans + qpow(a, b, M)) % M;
        }
        cout << ans << endl;
    }
}

C题：64位整数乘法

链接：https://ac.nowcoder.com/acm/contest/996/C

思路：

类似快速幂的思想，把整数b用二进制表示，即

[b = c_{k - 1}2^{k - 1} + c_{k -2}2^{k - 2} + ... + c_02^0 ]

typedef long long ll;
int main() {
	//freopen("in.txt", "r", stdin);
	ios::sync_with_stdio(false), cin.tie(0);
	ll a, b, p; cin >> a >> b >> p;
	ll ans = 0;
	for (; b; b >>= 1) {
		if (b & 1)ans = (ans + a) % p;
		a = (a << 1) % p;
	}
	cout << ans << endl;
}

⭐D题：最短Hamilton路径

链接：https://ac.nowcoder.com/acm/contest/996/D

解题思路

AC代码：

#define ms(a,b) memset(a,b,sizeof a)
int e[21][21], b[1 << 21][21], n;
int main() {
	//freopen("in.txt", "r", stdin);
	ios::sync_with_stdio(false), cin.tie(0);
	cin >> n;
	for (int i = 0; i < n; ++i)
		for (int j = 0; j < n; ++j)
			cin >> e[i][j];
	ms(b, 0x3f); b[1][0] = 0;
	for (int i = 0; i < 1 << n; ++i)
		for (int j = 0; j < n; ++j) if (i >> j & 1)
			for (int k = 0; k < n; ++k) if (~(i >> k) & 1)//if ((i ^ 1 << j) >> k & 1)
				b[i + (1 << k)][k] = min(b[i + (1 << k)][k], b[i][j] + e[j][k]);
	cout << b[(1 << n) - 1][n - 1] << endl;
}

⭐例题：[NOI2014]起床困难综合征

题意：

链接：[NOI2014] 起床困难综合症

贪心从高位到低位枚举，检验当前位在初始值为(0) 情况下的答案是否可以为(1) ，如果不能则检验当前位初始值能否为 (1)，并检验当前位在初始值为 (1) 情况下的答案是否可以为 (1)。

int n, m, x;
string str;
pair<string, int> a[100005];
int work(int bit, int now) {  // 用参加的第 bit 位进行n次运算
    for (int i = 1; i <= n; ++i) {
        int x = a[i].second >> bit & 1;
        if (a[i].first == "AND")
            now &= x;
        else if (a[i].first == "OR")
            now |= x;
        else
            now ^= x;
    }
    return now;
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> str >> x;
        a[i] = make_pair(str, x);
    }
    int val = 0, ans = 0;
    for (int bit = 29; bit >= 0; bit--) {
        int res0 = work(bit, 0), res1 = work(bit, 1);
        if (val += (1 << bit) <= m && res0 < res1)
            val += (1 << bit), ans += (res1 << bit);
        else
            ans += (res0 << bit);
    }
    cout << ans << "
";
    return 0;
}

0x02 递推与递归

递归实现指数型枚举

int _, n, m, k, x, y;
vector<int> vec;

void calc(int x) {
    if (x == n + 1) {
        for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
        cout << "
";  // 注意一下，以后输出回车用 "
" 而不是 endl
        return;
    }
    calc(x + 1), vec.push_back(x);
    calc(x + 1), vec.pop_back();
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n;
    calc(1);
}

递归实现组合型枚举

int n, m;
vector<int> vec;
void calc(int x) {
    // 剪枝，如果已经选取了超过m个数，
    // 或者即使选上剩下所有数也不够m个就要提前结束搜索了 ↓
    if (vec.size() > m || vec.size() + (n - x + 1) < m) return;
    if (x == n + 1) {
        for (int i = 0; i < vec.size(); ++i) cout << vec[i] << " ";
        cout << "
";  // 注意一下，以后输出回车用 "
" 而不是 endl
        return;
    }
    calc(x + 1), vec.push_back(x);
    calc(x + 1), vec.pop_back();
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;
    calc(1);
}

递归实现排列型枚举

int n, m;
int order[20];
bool chosen[20];
void cal(int k) {
	if (k == n + 1) {
		for(int i = 1;i<=n;++i)
			cout << order[i] << " ";
		cout << endl; return;
	}
	for (int i = 1;i <= n; ++i) {
		if (chosen[i])continue;
		chosen[i] = true;
		order[k] = i;
		cal(k + 1);
		chosen[i] = false;
	}
}
int main() {
	ios::sync_with_stdio(false), cin.tie(0);
	cin >> n;cal(1);
}

费解的开关

const int N = 6;//因为后续操作读取的是字符串 char g[N][N];char backup[N][N];//备份     --- 用于记录每次枚举第1行的情况int n;int dx[5] = {-1,0,1,0,0}, dy[5] = {0,0,0,-1,1};//用于表示当前位置及该位置的上下左右位置的偏移量 //改变当前灯及其上下左右灯的状况void turn(int x, int y){    for(int i = 0; i < 5; i ++){        int a = x + dx[i], b = y + dy[i];//用于表示当前位置或该位置的上下左右位置        if(a >= 0 && a < 5 || b >= 0 && b < 5){            g[a][b] ^= 1;//用于'0' 和'1'的相互转换     -----根据二者的Ascll码值特点        }    }} int main(){    cin >> n;    while(n --){        for(int i = 0; i < 5; i ++) cin >> g[i];//读取数据         int res = 10;//用于记录操作的结果        for(int op = 0; op < 32; op ++){//枚举第1行灯的状态 ---- 也可以采用递归实现指数型枚举            int step = 0;//用于记录当前情况的操作步数            memcpy(backup, g, sizeof g);//备份原数组数据  ----  因为每次枚举都是一种全新的情况             //枚举第一行，若灯灭，则点亮            for(int j = 0; j < 5; j ++){                if(!(op >> j & 1)){//也可以是 if(op >> j & 1) ,因为二者情况数量相同                    step ++;                    turn(0, j);//翻转当前灯的状况                }            }             //从第一行向下递推至倒数第二行            for(int i = 0; i < 4; i ++){                for(int j = 0; j < 5; j ++){                    if(g[i][j] == '0'){//当前行当前位置灯灭                        step ++;                        turn(i + 1, j);//改变当前行的下一行该列灯的状况，使当前行灯亮                    }                }            }             //检验最后一行灯是否全亮,若存在暗灯，则此方案不成立            bool dark = false;            for(int j = 0; j < 5; j ++){                if(g[4][j] == '0'){                    dark = true;                    break;                }            }             if(!dark) res = min(step, res);            memcpy(g, backup, sizeof backup);//还原数据,用于下次方案的操作        }         if(res > 6) res = -1;        cout << res << endl;    }    return 0;}

// 另一种解int _, a[6], ans, aa[6];string s;void dj(int x, int y) {    aa[x] ^= (1 << y);    if (x != 1) aa[x - 1] ^= (1 << y);    if (x != 5) aa[x + 1] ^= (1 << y);    if (y != 0) aa[x] ^= (1 << (y - 1));    if (y != 4) aa[x] ^= (1 << (y + 1));}void pd(int p) {    int k = 0;    memcpy(aa, a, sizeof(a));    for (int i = 0; i < 5; ++i)        if (!((p >> i) & 1)) {            dj(1, i);            if (++k >= ans) return;        }    for (int x = 1; x < 5; ++x)        for (int y = 0; y < 5; ++y)            if (!((aa[x] >> y) & 1)) {                dj(x + 1, y);                if (++k >= ans) return;            }    if (aa[5] == 31) ans = k;}int main() {    ios_base::sync_with_stdio(false), cin.tie(0);    for (cin >> _; _--;) {        memset(a, 0, sizeof(a));        for (int i = 1; i <= 5; ++i) {            cin >> s; // 字符串读入更便利处理            for (int j = 1; j <= 5; ++j) a[i] = a[i] * 2 + (s[j - 1] - '0');        }        ans = 7;        for (int p = 0; p < (1 << 5); p++) pd(p);        cout << (ans == 7 ? -1 : ans) << "
";    }    return 0;}

Strange Towers of Hanoi

#define Fi(i, a, b) for (int i = a; i <= b; ++i)int d[13], f[13];int main() {    ios_base::sync_with_stdio(false), cin.tie(0);    Fi(i, 1, 12) d[i] = d[i - 1] * 2 + 1;    memset(f, 0x3f, sizeof f), f[1] = 1;    Fi(i, 2, 12) Fi(j, 1, i) f[i] = min(f[i], 2 * f[j] + d[i - j]);    Fi(i, 1, 12) cout << f[i] << "
";    return 0;}

⭐Sumdiv （AcWing 97. 约数之和）（数论）（分治）

const int p = 9901;int pow(int x, int y) {    int ret = 1;    for (; y; y >>= 1) {        if (y & 1) ret = 1ll * ret * x % p;        x = (ll)x * x % p;    }    return ret;}int main() {    ios::sync_with_stdio(false), cin.tie(0);    int a, b, ans = 1;    cin >> a >> b;    if (!a) return !puts("0");    for (int i = 2, num; i * i <= a; i++) {        num = 0;        while (a % i == 0) a /= i, num++;        if (num)            ans =                ans * (pow(i, num * b + 1) - 1 + p) % p * pow(i - 1, p - 2) % p;    }    if (a > 1) ans = ans * (pow(a, b + 1) - 1 + p) % p * pow(a - 1, p - 2) % p;    cout << ans << "
";    return 0;}

⭐Fractal Streets

题解来源：Click Here

题意：
　　 给你一个原始的分形图,t组数据,对于每组数据,输入3个数n,h,o (n为在第n级,h,o为两个房子的编号),求在第n级情况下,编号为h和o的两个点之间的距离*10为多少。
　　其中,第n级分形图形成规则如下:

1. 首先先在右下角和右上角复制一遍n-1情况下的分形图
2. 然后将n-1情况下的分形图顺时针旋转90度,放到左上角
3. 最后将n-1情况下的分形图逆时针旋转90度 ,放到左下角
   编号是从左上角那个点开始计1,沿着道路计数。

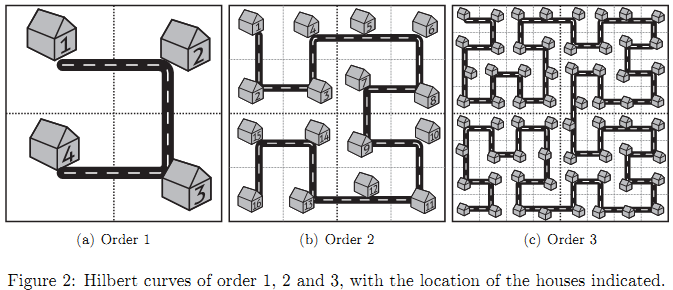
这是著名的通过一定规律无限包含自身的分形图。为了计算方便，我们将题目中房屋编号从0开始编号，那么S与D也都减掉1.
大体思路：设calc(n,m)求编号为m的房屋编号在n级城市中的坐标位置,那么距离是：calc(n,s-1) 与 calc(n,d-1)的距离。
从n(n > 1)级城市由四座n-1级城市组成，其中：
　　1.左上的n-1级城市由城市结构顺时针旋转90度，从编号的顺序看，该结构还做水平翻转，坐标转换至n级时如下图。
　　2与3.右上和右下和原始城市结构一样，坐标转换至n级时如下图。

市由城市结构逆时针旋转90度，从编号的顺序看，该结构也做了水平翻转。
　
　　旋转坐标的变化可通过公式：

　(设len = 2(n-1))当旋转角度是逆时针90度时，也就是顺时针270度时，（x，y）->(y, -x),然后再进行水平翻转，（y,-x）->(-y,-x)。然后再将图形平移到n级图形的左下角，在格子上的坐标变化是，水平方向增加len - 1个位置，垂直方向增加2len - 1个位置。因此坐标（x,y）按照规则转移到了（2len-1-y,len-1-x）.
　　注意：n-1级格子里拥有的房子数量是cnt = 22n /4,即22n-2.
　　　　当前编号m在N级格子的哪个方位是：m / cnt.
　　　　当前编号m在n-1级格子里的编号是: m %cnt;
详细代码如下：

using ll = long long;
pair<ll, ll> calc(ll n, ll m) {
    if (n == 0) return make_pair(0, 0);  //边界
    ll len = 1ll << (n - 1), cnt = 1ll << (2 * n - 2);
    pair<ll, ll> zb = calc(n - 1, m % cnt);
    ll x = zb.first, y = zb.second;
    ll z = m / cnt;
    switch (z) {
        case 0: return make_pair(y, x); break;
        case 1: return make_pair(x, y + len); break;
        case 2: return make_pair(x + len, y + len); break;
        case 3: return make_pair(2 * len - y - 1, len - x - 1); break;
    }
}
int main() {
    int t;
    cin >> t;
    while (t--) {
        ll n, s, d;
        cin >> n >> s >> d;
        pair<ll, ll> zb;
        pair<ll, ll> bz;
        double ans = 0;
        zb = calc(n, s - 1);  //记得-1 QWQ
        bz = calc(n, d - 1);
        ll x, y;
        x = (zb.first - bz.first), y = (zb.second - bz.second);  //边长居然是10
        ans = sqrt(x * x + y * y) * 10;  //喜闻乐见 勾股定理
        printf("%.0f
", ans);           //四舍五入
    }
    return 0;
}

非递归实现组合型枚举

#include <iostream>
#include <vector>
using namespace std;
vector<int> chosen;
int n, m;
void dfs(int x);
int main() {
    cin >> n >> m;
    dfs(1);
}
void dfs(int x) {
    if (chosen.size() > m || chosen.size() + (n - x + 1) < m) return;
    if (x == n + 1) {
        // if(chosen.size() == 0) return;
        for (int i = 0; i < chosen.size(); i++) printf("%d ", chosen[i]);
        puts("");
        return;
    }
    chosen.push_back(x);
    dfs(x + 1);
    chosen.pop_back();
    dfs(x + 1);
    return;
}

0x03 前缀和与差分

A题：HNOI2003]激光炸弹

按照蓝书上的教程做即可，注意这道题卡空间用int 而不是 long long。

int g[5010][5010];
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int N, R;
    cin >> N >> R;
    int xx = R, yy = R;
    for (int i = 1; i <= N; ++i) {
        int x, y, w;
        cin >> x >> y >> w, ++x, ++y;
        g[x][y] = w, xx = max(xx, x), yy = max(y, yy);
    }
    for (int i = 1; i <= xx; ++i)
        for (int j = 1; j <= yy; ++j)
            g[i][j] = g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1] +
                      g[i][j];  //求前缀和
    int ans = 0;
    for (int i = R; i <= xx; ++i)
        for (int j = R; j <= yy; ++j)
            //用提前算好的前缀和减去其他部分再补上多剪的那部分
            ans =
                max(ans, g[i][j] - g[i - R][j] - g[i][j - R] + g[i - R][j - R]);
    cout << ans << "
";
    return 0;
}

B题：IncDec Sequence

设 a 的差分序列为 b.

则对区间 [l, r] 的数都加 1，就相当于 b[l]++, b[r + 1]--.

操作分为 4 种.

① 2 ≤ l ≤ r ≤ n （区间修改）

② 1 == l ≤ r ≤ n（修改前缀）

③ 2 ≤ l ≤ r == n + 1 （修改后缀）

④ 1 == l ≤ r == n + 1 （全修改）

其中操作 ④ 显然无用.

操作 ① 性价比最高.

于是可得出方案：先用操作 ① ，使得只剩下 正数 或 负数 ，剩下的用操作 ② 或 ③ 来凑.

using ll = long long;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int n;
    cin >> n;
    vector<ll> a(n + 1, 0), b(n + 2);
    for (int i = 1; i <= n; ++i) cin >> a[i], b[i] = a[i] - a[i - 1];
    ll p = 0, q = 0;
    for (int i = 2; i <= n; ++i) {  // 2~n的正负数和统计
        if (b[i] > 0) p += b[i];
        else if (b[i] < 0) q -= b[i];
    }
    cout << max(p, q) << "
" << llabs(p - q) + 1 << "
";
    return 0;
}

C题：Tallest Cow

差分数组，对于给出第一个区间a,b,他们之间的人肯定比他们矮，最少矮1，那么就在a+1位置-1，b位置加1，计算前缀和，a+1以及之后的都被-1了，b及以后的不变。

重复的区间，不重复计算。

另一种思路：先将所有的牛的高度都设为最大值 然后在输入一组数A B时 将A B之间的牛的高度都减一。

map<pair<int, int>, bool> vis;
int c[10010], d[10010];
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int n, p, h, m;
    cin >> n >> p >> h >> m;
    while (m--) {
        int a, b;
        cin >> a >> b;
        if (a > b) swap(a, b);
        if (vis[make_pair(a, b)]) continue; // 避免重复计算
        vis[{a, b}] = true, d[a + 1]--, d[b]++;
    }
    for (int i = 1; i <= n; ++i) {
        c[i] = c[i - 1] + d[i];
        cout << h + c[i] << "
";
    }
    return 0;
}

0x04 二分

⭐二分A题：Best Cow Fences

二分答案，判定是否存在一个长度不小于L的子段，平均数不小于二分的值。如果把数列中的每个数都减去二分的值，就转换为判定“是否存在一个长度不小于L的子段，子段和非负”。

先分别考虑两种情况的解法（1、子段和最大【无长度限制】，2、子段和最大，子段长度不小于L）

<==>求一个子段，使得它的和最大，且子段的长度不小于L。

子段和可以转换为前缀和相减的形式，即设(sumj)表示(Ai 到 Aj)的和，

则有：(max{A[j+1]+A[j+2].......A[i] } ( i-j>=L ) \ = max{ sum[i] - min{ sum[j] }(0<=j<=i-L) }（L<=i<=n）)

仔细观察上面的式子可以发现，随着i的增长，j的取值范围 0~i-L 每次只会增大1。换言之，每次只会有一个新的取值进入 (min{sum_j}) 的候选集合，所以我们没必要每次循环枚举j，只需要用一个变量记录当前的最小值，每次与新的取值 sum[i-L] 取min 就可以了。

double a[100001], b[100001], sum[100001];int main() {    ios_base::sync_with_stdio(false), cin.tie(0);    int n, L;    cin >> n >> L;    for (int i = 1; i <= n; ++i) cin >> a[i];    double eps = 1e-5;    double l = -1e6, r = 1e6;    while (r - l > eps) {        double mid = (l + r) / 2;        for (int i = 1; i <= n; ++i) b[i] = a[i] - mid;        for (int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + b[i];        double ans = -1e10;        double min_val = 1e10;        for (int i = L; i <= n; ++i) {            min_val = min(min_val, sum[i - L]);            ans = max(ans, sum[i] - min_val);        }        if (ans >= 0)            l = mid;        else            r = mid;    }    cout << int(r * 1000) << "
";    return 0;}

0x05 排序

A题： Cinema

经典离散化例题，把电影的语言与字幕和观众懂的语言放进一个数组，然后离散化。

最后统计快乐人数。

const int N = 200006;int n, m, a[N], x[N], y[N], cinema[N * 3], tot = 0, k, ans[N * 3];int find(int f) { return lower_bound(cinema + 1, cinema + k + 1, f) - cinema; }int main() {    cin >> n;    for (int i = 1; i <= n; ++i) cin >> a[i], cinema[++tot] = a[i];    cin >> m;    for (int i = 1; i <= m; ++i) cin >> x[i], cinema[++tot] = x[i];    for (int i = 1; i <= m; ++i) cin >> y[i], cinema[++tot] = y[i];    sort(cinema + 1, cinema + tot + 1);    k = unique(cinema + 1, cinema + tot + 1) - (cinema + 1);    memset(ans, 0, sizeof(ans));    for (int i = 1; i <= n; i++) ans[find(a[i])]++;    int ans0 = 1, ans1 = 0, ans2 = 0;    for (int i = 1; i <= m; i++) {        int ansx = ans[find(x[i])], ansy = ans[find(y[i])];        if (ansx > ans1 || (ansx == ans1 && ansy > ans2)) {            ans0 = i;            ans1 = ansx;            ans2 = ansy;        }    }    cout << ans0 << endl;    return 0;}

当然不用离散化也可以做。

简单使用 unordered_map 映射个数即可

const int N = 2e5 + 10;int _, n, x, y, tmp, a[N];unordered_map<int, int> mp;int main() {    ios_base::sync_with_stdio(false), cin.tie(0);    for (cin >> _; _--;) cin >> tmp, mp[tmp]++;    cin >> n;    for (int i = 1; i <= n; ++i) cin >> a[i];    for (int i = 1; i <= n; ++i) {        int t;        cin >> t;        if (mp[a[i]] > x)            tmp = i, x = mp[a[i]], y = mp[t];        else if (mp[a[i]] == x && mp[t] > y)            tmp = i, y = mp[t];    }    cout << tmp << "
";    return 0;}

B题：货仓选址

排序一下，利用中位数的性质

int n, ans, sum;int main() {    ios_base::sync_with_stdio(false), cin.tie(0);    cin >> n;    vector<int> v(n);    for (auto &t : v) cin >> t;    sort(v.begin(), v.end());    ans = v[n / 2];    for (auto &t : v) sum += abs(t - ans);    cout << sum << "
";    return 0;}

C题：⭐七夕祭

这里借下 洛凌璃dalao的blog题解

题解

这个题其实是两个问题:

1.让摊点上下移动,使得每行的摊点一样多

2.左右移动摊点,使得每列的摊点一样多

两个问题是等价的,就讨论第一个

r[i]表示每行的摊点数

然后使得r[i]的一些摊点移动到r[i - 1]和r[i + 1], 类似于"均摊纸牌"

均摊纸牌

有M个人排一排,每个人分别有C[1]~C[M]张拍,每一步中,一个人可以将自己的一张手牌给相邻的人,求至少需要几步

显然, 纸牌总数T能被M整除有解,在有解的情况下, 考虑第一个人:

1.C[1] >= T/M, 第一个人要给第二个人C[1] - T/M张牌
2.C[1] < T/M, 第二个给第一个人T/M - C[1]张牌
本质就是使得第一人满足要求要|T/M - C[1]|步
那么满足第二人就要 |T/M - (C[2] - (T/M - C[1]))| = |2 * T/M - (C[1] + C[2])|步
满足第三人 |T/M - (C[3] - (T/M - (C[2] - (T/M - C[1]))))| = |3 * T/M - (C[1] + C[2] + C[3])|

到这里就可以发现,有一段是前缀和, 但再仔细化简以下可以发现

|3 * T/M - (C[1] + C[2] + C[3])|
=|(T/M - C[1]) + (T/M - C[2]) + (T/M - C[3])|
=|(C[1] - T/M) + (C[2] - T/M) + (C[3] - T/M)|

我们可以让A[i] = C[i] - T/M, S[i]为A[i]的前缀和,

那么对于"均摊纸牌"这道题的答案就是

∑ni=1∑i=1n|S[i]|

对于本题来说,无非是变成了环形问题

直接无脑dp就可以

我们随便选取一个人k最为断环的最后一名(即第一个人变为为k + 1),

则从这个人开始的持有的牌数(这行的摊点数), 前缀和为

A[k + 1]   S[k + 1] - S[k]A[k + 2]   S[k + 2] - S[k]...A[M]       S[M] - S[k]A[1]       S[M] - S[k] + S[1]A[2]       S[M] - S[k] + S[2]...A[k]       S[M] - S[k] + S[k]

我们发现S[M] = 0, 所以答案为

|S[k + 1] - S[k]| + ... + |S[M] - S[k]| + |s[M] - S[k] + S[1]| + ... + |S[M] - S[K] + S[k]|

=|S[k + 1] - S[k]| + ... + |S[M] - S[k]| + |-S[k] + S[1]| + ... + |-S[k] + S[k]|

=∑ni=1∑i=1n |S[i] - S[k]|

答案已经很明显了,像不像"仓货选址"?

仓货选址

一条轴上有N家店,每家店的坐标为D[1]~D[N],选择一家点为仓库向其他商店发货,求选哪家店,运送距离最短

不就是∑ni=1∑i=1n |D[i] - D[k]| 为答案吗?

当然是选中位数了啦,

设k左边有P家店,右边有Q家店

如果P<Q,那必然将k右移, ans - Q + P,答案明显变小了

Q>P,同理,故选择中位数

所以本题的答案就已经近在眼前了, 前缀和,求中位数

using ll = long long;
const int maxn = 1e5 + 5;
int n, m, k;
int c[maxn], r[maxn], s[maxn];

ll work(int a[], int n) {
    for (int i = 1; i <= n; ++i) s[i] = s[i - 1] + a[i] - k / n;
    sort(s + 1, s + 1 + n);
    ll ans = 0;
    for (int i = 1; i <= n; ++i) ans += abs(s[i] - s[(n >> 1) + 1]);
    return ans;
}

int main() {
    cin >> n >> m >> k;
    for (int i = 1; i <= k; ++i) {
        int a, b;
        cin >> a >> b, ++c[b], ++r[a];
    }
    if (k % n + k % m == 0)
        cout << "both " << work(c, m) + work(r, n);
    else if (k % n == 0)
        cout << "row " << work(r, n);
    else if (k % m == 0)
        cout << "column " << work(c, m);
    else
        cout << "impossible";
    return 0;
}

0x06 倍增

⭐例题 Genius_ACM

考虑到二分会有很多低效的操作（如：二分第一步检验 ([N - L] / 2) 这么长一段但右端点只会移动很少的部分），直接换倍增写。

1. 初始化 (p = 1,R = L)
2. 求出 ([L,R + p]) 区间的“检验值” ,若 检验值 (le T) 则 (R += p,p *=2) ，否则 (p /=2)
3. 重复上一步直到 (p = 0) ，此时 R 为所求值

#include <bits/stdc++.h>
using namespace std;
using ll    = long long;
const int N = 500006;
int n, m, w;
ll k, a[N], b[N], c[N];

void gb(int l, int mid, int r) {
    int i = l, j = mid + 1;
    for (int k = l; k <= r; k++)
        if (j > r || (i <= mid && b[i] <= b[j])) c[k] = b[i++];
        else
            c[k] = b[j++];
}

ll f(int l, int r) {
    if (r > n) r = n;
    int t = min(m, (r - l + 1) >> 1);
    for (int i = w + 1; i <= r; i++) b[i] = a[i];
    sort(b + w + 1, b + r + 1);
    gb(l, w, r);
    ll ans = 0;
    for (int i = 0; i < t; i++)
        ans += (c[r - i] - c[l + i]) * (c[r - i] - c[l + i]);
    return ans;
}

void Genius_ACM() {
    cin >> n >> m;
    cin >> k;
    for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
    int ans = 0, l = 1, r = 1;
    w    = 1;
    b[1] = a[1];
    while (l <= n) {
        int p = 1;
        while (p) {
            ll num = f(l, r + p);
            if (num <= k) {
                w = r = min(r + p, n);
                for (int i = l; i <= r; i++) b[i] = c[i];
                if (r == n) break;
                p <<= 1;
            } else
                p >>= 1;
        }
        ans++;
        l = r + 1;
    }
    cout << ans << endl;
}

int main() {
    int t;
    cin >> t;
    while (t--) Genius_ACM();
    return 0;
}

0x30 数学知识

0x31 质数

【例题】质数距离

【例题】阶乘分解

0x32 约数

AcWing 198. 反素数

AcWing 199. 余数之和

AcWing 200. Hankson的趣味题

AcWing 201. 可见的点

0x33 同余

AcWing 202. 最幸运的数字

AcWing 203. 同余方程

AcWing 204. 表达整数的奇怪方式

0x34 矩阵乘法

AcWing 205. 斐波那契

AcWing 206. 石头游戏

0x35 高斯消元与线性空间

AcWing 207. 球形空间产生器

AcWing 208. 开关问题169人打卡

AcWing 209. 装备购买

AcWing 210. 异或运算

0x36 组合计数

AcWing 211. 计算系数

AcWing 212. 计数交换

AcWing 213. 古代猪文

0x37 容斥原理与Mobius函数

AcWing 214. Devu和鲜花

AcWing 215. 破译密码

0x38概率与数学期望

AcWing 216. Rainbow的信号

AcWing 217. 绿豆蛙的归宿

AcWing 218. 扑克牌

0x39 0/1分数规划

0x40 博弈论之SG函数

AcWing 219. 剪纸游戏

0x50 动态规划

0x51 线性DP

【例题】Mr. Young's Picture Permutations

容易发现最高的人只能站在最左上角，然后后面的人从高到低必须要站在已经有的人的附近，不然就不合法。
以此为依据，以人数为阶段，每一排的人数为状态转移即可。可以使用队列保证状态转移顺序正确。

详细操作

事实上这个题考的是一个叫做杨氏矩阵的数据结构，有兴趣的话可自行了解。

using ll = long long;
int n[6], k;
void solve() {
    for (int i = 1; i <= k; ++i) cin >> n[i];
    while (k < 5) n[++k] = 0;
    ll f[n[1] + 1][n[2] + 1][n[3] + 1][n[4] + 1][n[5] + 1];
    memset(f, 0, sizeof(f));
    f[0][0][0][0][0] = 1;
    for (int i = 0; i <= n[1]; i++)
        for (int j = 0; j <= n[2]; j++)
            for (int k = 0; k <= n[3]; k++)
                for (int l = 0; l <= n[4]; l++)
                    for (int m = 0; m <= n[5]; m++) {
                        if (i < n[1]) f[i + 1][j][k][l][m] += f[i][j][k][l][m];
                        if (j < n[2] && i > j)
                            f[i][j + 1][k][l][m] += f[i][j][k][l][m];
                        if (k < n[3] && j > k)
                            f[i][j][k + 1][l][m] += f[i][j][k][l][m];
                        if (l < n[4] && k > l)
                            f[i][j][k][l + 1][m] += f[i][j][k][l][m];
                        if (m < n[5] && l > m)
                            f[i][j][k][l][m + 1] += f[i][j][k][l][m];
                    }
    cout << f[n[1]][n[2]][n[3]][n[4]][n[5]] << endl;
}

【例题】LCIS

LCS + LIS 综合考虑的问题，即求两个序列的最长公共上升子序列。

仿照求最长公共子序列和最长上升子序列的做法，定义 (f[i][j]) 为序列 (A) 中前 i 个元素和序列 (B) 以 j 为结尾的最长公共上升子序列，状态转移方程：

[f(i,j) = left{egin{matrix} & {f(i,j) = f(i - 1,j),quad if:A_i e B_j\ & f(i,j) = max_{0le k< j,B_k< B_j}{f(i - 1,k) + 1 = max_{0le k <j,B_k<A_i}{f(i - 1,k) + 1}} end{matrix} ight. ]

一般可以写三层循环来完成递推,

for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) {
            if (a[i] == b[j]) {
                for (int k = 0; k < j; ++k)
                    if (b[k] < a[i]) f[i][j] = max(f[i][j], f[i - 1][k] + 1);
            } else
                f[i][j] = f[i - 1][j];
        }

但 (max_{0le k< j,B_k< B_j}{f(i - 1,k) + 1) 这一部分只与当前的 (a[i]) 和之前的 (b[j]) 有关可以对于每个 i 单独维护它的值，最终时间复杂度为 (O(n^2)).

#include <bits/stdc++.h>
using namespace std;
const int N = 3001;
int ans, n, a[N], b[N], f[N];
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];
    for (int i = 1; i <= n; i++)
        for (int j = 1, val = 0; j <= n; j++)
            if (a[i] == b[j]) f[j] = val + 1;
            else if (b[j] < a[i])
                val = max(val, f[j]);
    for (int i = 1; i <= n; i++) ans = max(ans, f[i]);
    return printf("%d", ans), 0;
}

⭐Making the Grade

这道题强烈建议看书：P268

题目大意是给出一个长度为 n 的序列，要求使序列变为单调上升或单调不减序列（非严格），问花费的最少代价？

把 A 序列出现的数进行离散化，把DP状态中第二维 (j) 降到 (O(N))

转移方程是: (dp[i][j])表示前 (i) 个元素的最后一个元素为全部元素第 (j) 大时的最小代价

#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
int a[N], c[N], nums[N];
int f[N][N];
int n;
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        nums[i] = a[i];
    }
    sort(nums + 1, nums + n + 1);
    int m = unique(nums + 1, nums + n + 1) - nums - 1;
    for (int i = 1; i <= n; i++)
        c[i] = lower_bound(nums + 1, nums + m + 1, a[i]) - nums;
    memset(f, 0x3f, sizeof(f));
    f[0][0] = 0;
    for (int i = 1; i <= n; i++) {
        int temp = f[i - 1][0];
        for (int j = 1; j <= m; j++) {
            temp = min(temp, f[i - 1][j]);
            f[i][j] = temp + abs(a[i] - nums[j]);
        }
    }
    int ans = 1 << 30;
    for (int i = 1; i <= m; i++) ans = min(ans, f[n][i]);
    cout << ans << endl;
}

⭐Mobile Service

有3个员工起始在1,2,3个位置
他们要去p1,p2...pN按顺序完成任务 N<=2000,位置有200个
移动的代价为(c[x][p1]) 从x到p1
要求一个位置不能同时被两个员工占领

求完成所有P后代价最少为多少

显然阶段为Pi
需要记录3个状态,3个员工的位置,直接记录的话内存不够
我们可以发现在阶段i,必定有一个员工在pi,所以我们只需要记录另外两个员工的位置就好

void solve() {    //f[i][x][y] 表示完成了前i个任务，3个员工的位置分别为 x,y,p[i]的最小花费    f[0][1][2] = 0;    p[0]       = 3;    // 分别dp,从p[i-1]到p[i],x到p[i],y到p[i]    f[i][x][y]        = min(f[i][x][y], f[i - 1][x][y] + c(p[i - 1], p[i])) x != p[i], y != p[i];    f[i][p[i - 1]][y] = min(f[i][p[i - 1]][y], f[i - 1][x][y] + c(x, p[i])) p[i - 1] != p[i], y != p[i];    f[i][x][p[i - 1]] = min(f[i][x][p[i - 1]], f[i - 1][x][y] + c(y, p[i])) p[i - 1] != p[i], x != p[i];}

AC 代码

using ll    = long long;const int L = 210, N = 1010, inf = 0x3f3f3f3f;int l, n, c[L][L], p[N], f[N][L][L];void solve() {    memset(f, 0x3f, sizeof(f));    cin >> l >> n;    for (int i = 1; i <= l; ++i)        for (int j = 1; j <= l; ++j) cin >> c[i][j];    p[0]       = 3;    f[0][1][2] = 0;    for (int i = 1; i <= n; ++i) {        cin >> p[i];        for (int j = 1; j <= l; ++j)            for (int k = 1; k <= l; ++k) {                if (f[i - 1][j][k] != inf) {                    if (j != p[i] && k != p[i])                        f[i][j][k] = min(f[i][j][k], f[i - 1][j][k] + c[p[i - 1]][p[i]]);                    if (j != p[i] && p[i - 1] != p[i])                        f[i][j][p[i - 1]] =                            min(f[i][j][p[i - 1]], f[i - 1][j][k] + c[k][p[i]]);                    if (k != p[i] && p[i - 1] != p[i])                        f[i][p[i - 1]][k] =                            min(f[i][p[i - 1]][k], f[i - 1][j][k] + c[j][p[i]]);                }            }    }    int ans = inf;    for (int i = 1; i <= l; ++i)        for (int j = 1; j <= l; ++j) ans = min(ans, f[n][i][j]);    cout << ans;}

⭐传纸条

----------------------------
有这么一些状态
步数i,两个状态(x1,y1)(x2,y2)

我们考虑寻找能够覆盖整个状态空间的最小的 "维度集合" 

由于每次两个坐标只能走一次
所以我们可以观察到步数和坐标之间的关系有:
i+2 = x1+y1 = x2+y2
所以我们可以维护3个状态f[横纵坐标和][x1][x2]
那么可以通过横纵坐标和 以及 x1,x2
求出(x1,y1),(x2,y2)

转移方程:
每个点可以有前面的两个点转移过来,2*2=4
所以每个状态可以由四种状态转移过来,取最大

f[x1][y1][x2][y2] <====
	max(f[x1-1][y1][x2-1][y2],
		f[x1-1][y1][x2][y2-1],
		f[x1][y1-1][x2-1][y2],
		f[x1][y1-1][x2][y2-1]) + a[x1][y1] + a[x2][y2];
对应为:
f[i][x1][x2] <=====
	max(f[i-1][x1-1][x2],f[i-1][x1-1][x2-1],
		f[i-1][x1][x2-1],f[i-1][x1][x2-1]) + a[x1][y1] + a[x2][y2];    

using ll    = long long;
const int N = 60;
int f[N << 1][N][N], a[N][N];
void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) cin >> a[i][j];
    for (int i = 0; i < n + m - 2; i++)
        for (int j = 1; j <= n && j <= i + 1; j++)
            for (int k = 1; k <= n && k <= i + 1; k++) {
                if (j == k) {
                    f[i + 1][j][k] =
                        max(f[i + 1][j][k], f[i][j][k] + a[j][i + 3 - j]);
                    f[i + 1][j + 1][k + 1] =
                        max(f[i + 1][j + 1][k + 1],
                            f[i][j][k] + a[j + 1][i + 2 - j]);
                } else {
                    f[i + 1][j][k] =
                        max(f[i + 1][j][k],
                            f[i][j][k] + a[j][i + 3 - j] + a[k][i + 3 - k]);
                    f[i + 1][j + 1][k + 1] = max(
                                                 f[i + 1][j + 1][k + 1],
                                                 f[i][j][k] + a[j + 1][i + 2 - j] + a[k + 1][i + 2 - k]);
                }
                if (j + 1 == k)
                    f[i + 1][j + 1][k] = max(f[i + 1][j + 1][k],
                                             f[i][j][k] + a[j + 1][i + 2 - j]);
                else
                    f[i + 1][j + 1][k] =
                        max(f[i + 1][j + 1][k],
                            f[i][j][k] + a[j + 1][i + 2 - j] + a[k][i + 3 - k]);
                if (k + 1 == j)
                    f[i + 1][j][k + 1] =
                        max(f[i + 1][j][k + 1], f[i][j][k] + a[j][i + 3 - j]);
                else
                    f[i + 1][j][k + 1] =
                        max(f[i + 1][j][k + 1],
                            f[i][j][k] + a[j][i + 3 - j] + a[k + 1][i + 2 - k]);
            }
    cout << f[n + m - 2][n][n] << endl;
}

⭐Cookies

CH5105 Cookies
圣诞老人共有M个饼干，准备全部分给N个孩子。每个孩子有一个贪婪度，
第 i 个孩子的贪婪度为 g[i]。如果有 a[i] 个孩子拿到的饼干数比第 i 个孩子多，
那么第 i 个孩子会产生 g[i]*a[i]的怨气。给定N、M和序列g，
圣诞老人请你帮他安排一种分配方式，使得每个孩子至少分到一块饼干，
并且所有孩子的怨气总和最小。1≤N≤30, N≤M≤5000, 1<=gi<=10^7。 
--------------------------------------------------------------------------
安排啊方案啊...N,M都比较小,可以DP，不会啊...
"已经获得饼干的孩子","已经发放的饼干",可以作为阶段
然后一个孩子的g值会影响他获得的饼干数

贪心策略的g值高的孩子获得的饼干数多
可以交换两个值进行比较证明.
设g[i]>g[i-1]>g[i-2]...
获得饼干 c[i]>c[i-1]>c[i-2]...
贡献值 X = 0*g[i]+1*g[i-1]+2*g[i-2]...
 
 g[i]>g[i-1]>g[i-2]...
获得饼干 c[i-1]>c[i]>c[i-2]...
贡献值 Y = 0*g[i-1]+1*g[i]+2*g[i-2]...
g[i] > g[i-1] 显然Y>X...故用X

a[i]为第i个孩子的饼干数 
对于第i+1个孩子饼干数有两种选择,要么等于第i个孩子,要么少于第i个孩子a[i+1]=i
可是我们必须知道a[i],但是很难维护....

画出饼干递减的柱形图
发现若第i个孩子饼干数大于1的话,
则等价于把前i个孩子的饼干数都减少1
因为饼干数的相对大小顺序不变,所以总贡献也不变
f[i][j] <=== f[i][j-i] 

然后,若第i个孩子的饼干数为1的话,
则枚举i前面有k个孩子的饼干数等于1
f[i][j] <=== min( f[k][j-(i-k)] + k*(g[k+1]~g[i]) )

0x52 背包

0x53 区间DP

0x54树形DP

0x55 环形与后效性处理

AcWing 288. 休息时间

题目描述
把一天划分为 (N) 个时间段，每天总共需要休息 (M) 个时间段，第 ii 时间段休息可以恢复 (u_i) 体力，每次休息过程中第一个时间段无法恢复体力。需要最大化每天能获得的体力。

解法
注：本题作为蓝书中的例题，代表了一类必须掌握的题型，推荐在参照题解前先尝试自己完成代码。

一道显然的 (DP) 题目。经过分析可得知每个时刻的最优解受到三个因素影响：当前时刻、当前总休息时间及当前时刻是否休息。因此我们用 (f_{i,j,k}=0/1) 表示状态，即第 (i) 时刻为止共休息 (j) 个时间段的最优解，(k) 表示当前时间段是否正在休息。

本题安排的休息时间可以跨越一天的最后一个时间段，即当天休息后第二天再醒来，因此本题的模型是一个环形模型。

处理环形模型一般使用分类讨论与断环为链两种解法，本篇题解重点介绍第一种。

不难发现，我们可以把安排的方案分为两种类型。

• 最后一个时间段不休息，此时本题转化为线性模型；
• 第一个时间段休息。

首先考虑第一种情况。线性模型求解不会受到后效性的影响，我们可以轻松写出对应的方程：

[f_{i,j,0} = max{f_{i-1,j,0},f_{i-1,j,1}}\ f_{i,j,1} = max{f_{i-1,j - 1,0},f_{i-1,j-1,1 + u_i}} ]

最终答案 (ans=max{f_{N,M,0},f_{N,M,1}})。

接着考虑第二种情况。我们发现这种情况与上文中的第一种情况几乎没有差异，唯一的不同点是在这种情况下第一时间段能够恢复一些体力，而上一种不可以。因此只需要强制令 (f_{i,1,1}=u_1)，重复上述过程即可。最终答案 (ans=max{ans,f_{N,M,1}}).

本题是否已经被完全解决了？也许并没有。本题的空间限制仅有64 MB，这样的代码一定会 MLE。因此需要考虑进一步的优化。

我们发现，在求(f_{i,j,k}) 的过程中只用到了 (f_{i−1,j,k}) 的值，与(i−1) 之前时刻的解无关。因此可以使用滚动数组优化，用 i&1 代替 (i)。这样一来，程序使用的空间大大减少，能够通过本题。

至此，本题得到完美解决。

注：切记(DP) 的边界条件与 (f) 数组的初始化。

有关环形模型的第二种处理方式，即断环为链，可以参考蓝书中的下一道例题： AcWing289 环路运输。

int n, b, ans = 0, T;
int f[2][3831][2], a[3831];
int Max(int a, int b) {return a > b ? a : b;}
int Min(int a, int b) {return a < b ? a : b;}
void solve() {
    cin >> n >> b;
    for (int i = 1; i <= n; ++i)cin >> a[i];
    memset(f, 128, sizeof(f));//初始化为负无穷
    f[1][0][0] = f[1][1][1] = 0;//边界条件
    // 第n小时不在睡觉,情况1
    for (int i = 2; i <= n; ++i)
        for (int j = 0; j <= Min(b, i); ++j) {
            f[i & 1][j][0] = Max(f[(i - 1) & 1][j][0], f[(i - 1) & 1][j][1]);
            if (j)f[i & 1][j][1] = Max(f[(i - 1) & 1][j - 1][0],
                                           f[(i - 1) & 1][j - 1][1] + a[i]);
        }
    ans = Max(ans, Max(f[n & 1][b][0], f[n & 1][b][1]));
    memset(f, 128, sizeof(f));
    f[1][1][1] = a[1];
    for (int i = 2; i <= n; i++) { //情况 2
        for (int j = 0; j <= Min(b, i); j++) {
            f[i & 1][j][0] = Max(f[(i - 1) & 1][j][0], f[(i - 1) & 1][j][1]);
            if (j)f[i & 1][j][1] = Max(f[(i - 1) & 1][j - 1][0],
                                           f[(i - 1) & 1][j - 1][1] + a[i]);
        }
    }
    ans = Max(ans, f[n & 1][b][1]);
    cout << ans << "
";
}

AcWing 289. 环路运输

题目描述
环上有 (N) 个点，每个点有点权 (A_i)，相邻仓库距离为 1，任意两点 i,j 之间的距离定义为沿环的两侧分别从 i 前往 j 的距离中的较小值。定义任意两点 i,j 之间的代价为 (A_i+A_j+dis_{i,j})，求环上最大代价。

解法
注：本题作为蓝书中的例题，代表了一类必须掌握的题型，推荐在参照题解前先尝试自己完成代码。

不难看出使用 (DP) 求解的基本思路。

本题为环状模型，处理起来有一定难度。处理环状模型有两种常用方法：分类讨论与断环为链。如想要了解分类讨论的思想，可以参照蓝书中的上一道例题 AcWing288 休息时间。下面主要介绍断环为链的思想。

断环为链的思想可以简述为：对于一个长度为 N 的环，我们不妨将其断开并延长一倍，使之变成一条长度为 2N 的链，并将其划分为若干部分分别考虑。

首先把题面中计算代价的算式拆开，可以得到：

[f_{i,j}=left{ egin{array}{**lr**} A_i+A_j+i−j & (j<i,i−j≤N/2) \ A_i+A_j+N+j−i & (j<i,i−j>N/2) end{array} ight. ]

在断环为链之后，该算式等价于：在长度为 2N 的链上，

[f_{i,j}=A_i+A_j+i−j (j<i,i-j le N/2 ]

此时，本题已经被转化为了标准的线性 DP。

下面我们考虑如何求解该线性模型。如果按照上文推出的算式进行 DP，我们需要一维枚举 i，一维枚举 j，总时间复杂度为 (O(N^2))。本题中 (N≤10^6)，这样的复杂度无法令人满意。考虑优化。

继续观察算式，我们发现该算式可以转化为如下形态：

[f_{i,j} = max{(A_j-j)+(A_i+i)} (j<i,i-jle N/2) ]

其中，当 (i) 固定时，((Ai+i)) 也确定了下来，我们只需要考虑 ((Aj−j)) 的最大值即可。

考虑对这一部分使用单调队列维护（参见蓝书 0x59 节）。通过这种方式，我们可以在 (O(1)) 的时间内得到这一部分的最大值。

均摊时间复杂度为 (O(N))，可以通过本题。

至此，本题得到完美解决。

using ll = long long;
const int N = 2e6 + 10;
int a[N], q[N], h = 1, t = 0, n;
ll ans;
void solve() {
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        a[i + n] = a[i];
    }
    int len = n / 2;
    q[++t] = 1;
    for (int i = 2; i <= n + len; ++i) {
        while (q[h] < i - len and h <= t)h++;
        ans = max(ans, 1ll * (a[i] + i + a[q[h]] - q[h]));
        while (a[q[t]] - q[t] < a[i] - i and t >= h)t--;
        q[++t] = i;
    }
    cout << ans;
}

0x59单调队列优化DP

AcWing 298. 围栏

状态转移依然不错
f[i][j]表示第i个木匠刷到j总共的报酬
将题中的木匠按 (s) 进行排序，只会更新 (j>=s) 的，保证没有后效性
(f[i][j]=max(f[i-1][j],f[i][j-1]);) 表示可以i木匠不刷或者当前的木板不刷
(f[i][j]=max( f[i][j],f[i-1][k]+p[i]*(j-k) ) j>=si,j-k>=li;)

当i固定时
寻找k的过程可以用单调队列优化
当j++时k的选择范围增加了1
将方程中与k有关的部分放到单调队列中
维护一个 (f[i-1][k]-p[i]*k) 单减,k单增的队列，即可完成转移

typedef pair<int, int> pii;
const int N = 16010, M = 110;
struct node {
	int l, p, s;
} a[M];
int n, m, dp[M][N];
bool cmp(node a, node b) { return a.s < b.s; }
void solve() {
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= m; ++i) cin >> a[i].l >> a[i].p >> a[i].s;
	sort(a + 1, a + 1 + m, cmp);
	for (int i = 1; i <= m; ++i) {
		deque<pii> q1;
		for (int j = 0; j <= n; ++j) {
			dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
			if (j >= a[i].s) {
				while (q1.size() and q1.front().second < j - a[i].l) q1.pop_front();
				if (q1.size()) dp[i][j] = max(dp[i][j],
					                              q1.front().first + a[i].p * j);
			} else {
				while (q1.size()
				        and q1.back().first <= dp[i - 1][j] - a[i].p * j) q1.pop_back();
				q1.push_back({dp[i - 1][j] - a[i].p * j, j});
			}
		}
	}
	cout << dp[m][n] << '
';
}