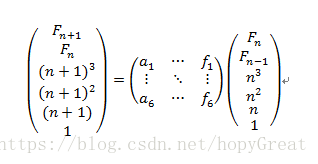2018年湘潭大学程序设计竞赛 重现赛

A. 时间统计

scanf 读入即可快速分割数据

using ll = long long;
void solve() {
    int D, h, m, s;
    ll T[2];
    for (int i = 0; i < 2; ++i) {
        scanf("%dday%02d:%02d:%02d", &D, &h, &m, &s);
        T[i] = D * 3600 * 24 + h * 3600 + m * 60 + s;
    }
    cout << T[1] - T[0] << "
";
}

B. String

凯少霸气单人Solo此题

const int N = 100010 ;
int col[7], row[7] ;
string cc[7] = {
    "012345",
    "6789AB",
    "CDEFGH",
    "IJKLMN",
    "OPQRST",
    "UVWXYZ"
};
string ex_cc[7] = {
    "06CIOU",
    "17DJPV",
    "28EKQW",
    "39FLRX",
    "4AGMSY",
    "5BHNTZ"
};
void solve() {
    string s ; cin >> s ;
    memset(col, 0, sizeof col) ;
    memset(row, 0, sizeof row) ;
    int max_col = -1, max_row = -1 ;
    for (int i = 0; i < s.size(); i++) {
        for (int j = 0; j < 6; j ++ ) if (cc[j].find(s[i]) < 7) col[j] ++ ;
        for (int j = 0; j < 6; j ++ ) if (ex_cc[j].find(s[i]) < 7) row[j] ++ ;
    }
    for (int i = 0; i < 6; i ++ ) max_col = max(max_col, col[i]) ;
    for (int i = 0; i < 6; i ++ ) max_row = max(max_row, row[i]) ;
    for (int i = 0; i < 6; i ++ )
        for (int j = 0; j < 6; j ++ )
            if (col[i] == max_col && row[j] == max_row)
                cout << cc[i][j] ;
    cout << endl ;
}

C. Boom

贺佬秒A

typedef  pair<int, int> pii;
map<vector<pii>, int> p;
void solve() {
    int n;
    cin >> n;
    p.clear();
    int a, b, c, d;
    while (n--) {
        cin >> a >> b >> c >> d;
        for (int i = a; i < c; i++) {
            for (int j = b; j < d; j++) {
                vector<pii> temp(2);
                temp[0].first = i, temp[0].second = j;
                temp[1].first = i + 1, temp[1].second = j + 1;
                p[temp]++;
            }
        }
    }
    int maxx = -1;
    for (auto &x : p) maxx = max(x.second, maxx);
    cout << maxx << endl;
}

D. Fibonacci进制

思路学习自千千dalao

因为我们要让这一个数 (x) 表示的最终结果最小，所以要将他展开的越彻底越好（注意不能出现相同的斐波那契数）

最好的情况下 (x) 刚好可以表示为前 (k) 项的斐波那契数的和减一（因为标准的斐波那契数列前面有两个重复的 (1) ）

于是我们有：(x = (sum_{i=1}^kFib[i]) - 1)

根据斐波那契数列的性质我们还有：(sum_{i = 1}^nFib[i] = Fib[n + 2]-1)

因此得出：(x = Fib[k+2]-2) 等价于 (x + 2 = Fib[k + 2])

打表求出 (10^9) 以内所有的斐波那契数，然后二分求出一个 (k) 使得 (x + 2le Fib[k + 2])。

• 对于特殊的情况 ((Fib[k+2]=k+2))：此时答案肯定为 (2^k-1)

• 对于一般的情况 ((Fib[k+2]>x+2))：

  我们需要从中去除可以组合出(Fib[k+2] - (x+2)) 的极大项（常识不加解释），最终所剩余的部分便是这道题的答案

using ll = long long;
ll f[52] = {
    1,          1,           2,           3,           5,          8,
    13,         21,          34,          55,          89,         144,
    233,        377,         610,         987,         1597,       2584,
    4181,       6765,        10946,       17711,       28657,      46368,
    75025,      121393,      196418,      317811,      514229,     832040,
    1346269,    2178309,     3524578,     5702887,     9227465,    14930352,
    24157817,   39088169,    63245986,    102334155,   165580141,  267914296,
    433494437,  701408733,   1134903170,  1836311903,  2971215073, 4807526976,
    7778742049, 12586269025, 20365011074, 32951280099,
};
void solve() {
    ll n;
    cin >> n;
    ll now = lower_bound(f, f + 52, n + 2) - f;
    ll cha = f[now] - n - 2;
    now = (1LL << (now - 2)) - 1;
    while (cha > 0) {
        ll sn = upper_bound(f, f + 52, cha) - 1 - f;
        now &= ~(1LL << (sn - 1));
        cha -= f[sn];
    }
    cout << now << "
";
}
}

E. 吃货

先对数组按价格排序，然后在比较美味值，如果更大则覆盖，在 [0,cnt] 二分搜索比零钱更多的点输出即可

typedef pair<int, int> pii;
const int N = 1e5 + 10, inf = 0x3f3f3f3f;
pii data[N];
void solve() {
    int n, m, cnt = 1;
    cin >> n >> m;
    for (int i = 0; i < n; ++i)cin >> data[i].first >> data[i].second;
    sort(data, data + n);
    for (int i = 1 ; i <= n; ++i)
        if (data[cnt - 1].second < data[i].second)data[cnt++] = data[i];
    ll v;
    while (m--) {
        cin >> v;
        int x = upper_bound(data, data + cnt, pii(v, inf)) - data;
        if (x - 1 < cnt and x - 1 >= 0)cout << data[x - 1].second << "
";
        else cout << "0
";
    }
}

G. 又见斐波那契 (矩阵快速幂)

这是一个加强版的斐波那契数列。

给定递推式

求F(n)的值，由于这个值可能太大，请对109+7取模。

说实话，这道题完全没想到是用矩阵快速幂做：一位dalao的讲解

这个相比普通的斐波那契数列多了后面四项，看一眼数据范围，使用普通的o（n）的算法肯定会超时，

因此这里需要使用矩阵快速幂（斐波那契数列的项数n一旦过大，就要考虑快速幂，普通算法时间空间都开销太大）。

使用矩阵快速幂的一个关键问题就是矩阵递推式。

参考普通快速幂那一片博客最后面的那个扩展式，就可以得到下面这个递推式了：

然后通过计算等价替换可得出该矩阵A：

下面只需要把普通斐波那契数列的构造由2*2的矩阵换为6*6的即可。

using ll = long long;
const int mod = 1e9 + 7;
const int N = 6;
ll tmp[N][N], res[N][N];
ll n;
void mul(ll a[][N], ll b[][N]) {
    memset(tmp, 0, sizeof(tmp));
    for (int i = 0; i < N; ++i)
        for (int j = 0; j < N; ++j)
            for (int k = 0; k < N; ++k) {
                tmp[i][j] += a[i][k] * b[k][j] % mod;
                if (tmp[i][j] >= mod) tmp[i][j] -= mod;
            }
    for (int i = 0; i < N; ++i)
        for (int j = 0; j < N; ++j)a[i][j] = tmp[i][j];
}
void pow(ll a[][N]) {
    memset(res, 0, sizeof(res));
    for (int i = 0; i < N; ++i)res[i][i] = 1;
    for (; n; n >>= 1) {
        if (n & 1)mul(res, a);
        mul(a, a);
    }
}
void solve() {
    cin >> n, n--;
    ll ans[N][N] = { 1, 1, 1, 1, 1, 1,
                     1, 0, 0, 0, 0, 0,
                     0, 0, 1, 3, 3, 1,
                     0, 0, 0, 1, 2, 1,
                     0, 0, 0, 0, 1, 1,
                     0, 0, 0, 0, 0, 1
                   };
    pow(ans);
    ll sum = 0;
    ll x[N] = {1, 0, 8, 4, 2, 1};
    for (int i = 0; i < N; ++i) {
        sum += (res[0][i] * x[i]) % mod;
        if (sum >= mod) sum -= mod;
    }
    cout << sum << "
";
}

H. 统计颜色

线段树一维区间更新和查询

#include<bits/stdc++.h>
#define ll long long
#define MAXN 400005
#define ls l,m,rt<<1
#define rs m+1,r,rt<<1|1
using namespace std;
ll sum[MAXN], add[MAXN];
void pushup(int rt) { sum[rt] = sum[rt << 1] | sum[rt << 1 | 1];}
void pushdown(int rt) {
    if (add[rt]) {
        add[rt << 1] |= add[rt];
        add[rt << 1 | 1] |= add[rt];
        sum[rt << 1] |= add[rt];
        sum[rt << 1 | 1] |= add[rt];
        add[rt] = 0;
    }
}

void update(int a, int b, ll v, int l, int r, int rt) {
    if (a <= l && b >= r) {
        add[rt] |= v;
        sum[rt] |= v;
        return ;
    }
    pushdown(rt);
    int m = (l + r) >> 1;
    if (a <= m) update(a, b, v, ls);
    if (m < b) update(a, b, v, rs);
    pushup(rt);
}

ll query(int a, int b, int l, int r, int rt)
{
    if (a <= l && b >= r)
        return sum[rt];
    pushdown(rt);
    int m = (l + r) >> 1;
    ll res = 0;
    if (a <= m) res |= query(a, b, ls);
    if (m < b)  res |= query(a, b, rs);
    return res;
}

int getc(ll g) {
    int ans = 0;
    while (g) {
        ans += g % 2;
        g = g / 2;
    }
    return ans;
}

int main() {
    int n, m, x, l, r;
    ll c;
    while (scanf("%d%d", &n, &m) != EOF) {
        memset(add, 0, sizeof(add));
        memset(sum, 0, sizeof(sum));
        for (int i = 1; i <= m; i++) {
            scanf("%d", &x);
            if (x == 1) {
                scanf("%d%d%lld", &l, &r, &c);
                c = 1LL << c;
                update(l, r, c, 1, n, 1);
            }
            else {
                scanf("%d%d", &l, &r);
                printf("%d
", getc(query(l, r, 1, n, 1)));
            }
        }
    }
    return 0;
}