蓝桥杯历年国赛真题汇总:Here
1.哥德巴赫分解
哥德巴赫猜想认为:不小于4的偶数都可以表示为两个素数的和。
你不需要去证明这个定理,但可以通过计算机对有限数量的偶数进行分解,验证是否可行。
实际上,一般一个偶数会有多种不同的分解方案,我们关心包含较小素数的那个方案。
对于给定数值范围,我们想知道这些包含较小素数方案中最大的素数是多少。
比如,100以内,这个数是19,它由98的分解贡献。
你需要求的是10000以内,这个数是多少?
答案:173
const int N = 10000;
vector<int>prime;
bool vis[10010];
int ans;
void check(int n) {
for (int i = 0; i < prime.size(); ++i) {
int r = n - prime[i];
if (vis[r]) {
ans = max(ans, prime[i]);
return ;
}
}
}
void solve() {
memset(vis, true, sizeof(vis));
for (int i = 2; i < N; ++i)
if (vis[i])for (int j = i + i; j < N; j += i)vis[j] = false;
for (int i = 2; i < N; ++i)if (vis[i])prime.push_back(i);
for (int i = 4; i < 10000; i += 2)check(i);
cout << ans << "
";
}
2.数字划分
w星球的长老交给小明一个任务:
1,2,3...16 这16个数字分为两组。
要求:
这两组数字的和相同,
并且,两组数字的平方和也相同,
并且,两组数字的立方和也相同。
请你利用计算机的强大搜索能力解决这个问题。
并提交1所在的那个分组的所有数字。
这些数字要从小到大排列,两个数字间用一个空格分开。
即类似:1 4 5 8 ... 这样的答案。
注意,只提交这一组数字,不要填写任何多余的内容。
笨笨有话说:
只要一个组的成员确定了,另一个组的成员也就确定了。枚举一个组的成员就可以了。
凭直觉,两个组的成员数目不会差太多吧。
歪歪有话说:
既然求 1 所在的那个组,那只要枚举剩余的成员就可以了。
貌似都是8个成员的可能性很大啊。
答案:1 4 6 7 10 11 13 16
爆搜
bool vis[17];
void dfs(int pos, int cnt) {
if (cnt == 8) {
int sum1 = 0, sum2 = 0, sum11 = 0, sum22 = 0;
for (int i = 1; i <= 16; ++i) {
if (!vis[i])sum1 += i * i, sum2 += i * i * i;
else sum11 += i * i, sum22 += i * i * i;
}
if (sum1 == sum11 and sum2 == sum22) {
for (int i = 1; i <= 16; ++i)if (!vis[i]) cout << i << " " ;
cout << "
"; return; // 找到一组就直接推出即可
}
return ;
}
for (int i = pos + 1; i <= 16; ++i) {
if (!vis[i])continue;
vis[i] = false;
dfs(i, cnt + 1);
vis[i] = true;
}
}
3.表达式计算
虽然我们学了许久的程序设计,但对于简单的四则混合运算式,如果让我们完全白手起家地编程来解析,还是有点棘手。
这里,我们简化一下问题,假设只有加法和乘法,并且没有括号来改变优先级。
再假设参加运算的都是正整数。
在这么多的限制条件下,表达式的解析似乎简单了许多。
下面的代码解决了这个问题。请仔细阅读源码,并填写划线部分缺少的代码。
#include <stdio.h>
int f3(const char* s, int begin, int end) {
int sum = 0;
int i;
for (i = begin; i < end; i++) {
if (s[i] == ' ') continue;
sum = sum * 10 + (s[i] - '0');
}
return sum;
}
int f2(const char* s, int begin, int end) {
int p = begin;
int pro = 1;
while (1) {
int p0 = p;
while (p != end && s[p] != '*') p++;
pro *= _______________________________; //填空
if (p == end) break;
p++;
}
printf("f2: pro=%d
", pro);
return pro;
}
int f(const char* s) {
int p = 0;
int sum = 0;
while (1) {
int p0 = p;
while (s[p] != 0 && s[p] != '+') p++;
sum += f2(s, p0, p);
if (s[p] == 0) break;
p++;
}
return sum;
}
int main() {
int x = f("12+18+5*4*3+10");
printf("%d
", x); // 100
return 0;
}
注意:只填写划线处缺少的内容,不要填写已有的代码或符号,也不要填写任何解释说明文字等。
答案:
f3(s, p0, p)仔细阅读代码即可
4.小数第n位
我们知道,整数做除法时,有时得到有限小数,有时得到无限循环小数。
如果我们把有限小数的末尾加上无限多个0,它们就有了统一的形式。
本题的任务是:在上面的约定下,求整数除法小数点后的第n位开始的3位数。
输入:
一行三个整数:a b n,用空格分开。a是被除数,b是除数,n是所求的小数后位置(0<a,b,n<1000000000)
输出:
一行3位数字,表示:a除以b,小数后第n位开始的3位数字。
比如:
输入:
1 8 1
程序应该输出:
125
再比如:
输入:
1 8 3
程序应该输出:
500
再比如:
输入:
282866 999000 6
程序应该输出:
914
提交时,注意选择所期望的编译器类型。
笨笨有话说:
这个除法小学就会算啊,模拟手算除法的过程就可以了吧。
只是数有点大啊....
管它呢,能算多远算多远....
歪歪有话说:
如果我能确定循环节从哪里开始到哪里结束,再大的数不过就是与它取模的余数等价啊
【思路】
模拟除法。
13 / 7 = 1.85714285...
这里求小数部分,所有取模忽略掉整数部分
13 / 7 -> 6 / 7
第一位:(小数点后第几位,以下同)6 * 10 / 7 = 8;
得到第一位后的余数:6 * 10 % 7 = 4
那么第二位:4 * 10 / 7 = 5
得到第二位后的余数:4 * 10 % 7 = 5
第三位:5 * 10 / 7 = 7
依此类推
void solve() {
ll a, b, n;
cin >> a >> b >> n;
a %= b;
while (n > 10) {
a *= 1E10; a %= b; n -= 10;
}
for (int i = 0; i < n + 2; ++i) {
a *= 10;
if (i >= n - 1)cout << a / b;
a %= b;
}
}
5.分考场
n个人参加某项特殊考试。
为了公平,要求任何两个认识的人不能分在同一个考场。
求最少需要分几个考场才能满足条件。
输入格式:
第一行,一个整数n(1<n<100),表示参加考试的人数。
第二行,一个整数m,表示接下来有m行数据
以下m行每行的格式为:两个整数a,b,用空格分开 (1<=a,b<=n) 表示第a个人与第b个人认识(编号从1开始)。
输出格式:
一行一个整数,表示最少分几个考场。
例如:
输入:
5
8
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5
程序应该输出:
4
再比如:
输入:
5
10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
则程序应该输出:
5
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
【思路】
一开始以为是并查集之类的连通图大小的问题,写了一发结果只通过 30% 的数据,重新审题发现其实就是图的着色问题:给定顶点数和边,求至少需要多少种颜色对图进行涂色能是相邻顶点颜色不同。
const int N = 110, inf = 0x3f3f3f3f;
int e[N][N];
int vis[N][N]; // vis[i][j] = t表示第i个考场里面第j个人是t
int cnt[N]; // 记录每个考场种的学生数量(对应的vis)
int ans = inf, n, m;
void dfs(int id, int num) {// id表示第id个学生,num表示当前考场编号
if (num >= ans)return;
if (id > n) { // 学生已经安排完了
ans = min(ans, num);// 更新当前最优解(不要用min可能超时)
return;
}
for (int i = 1; i <= num; ++i) {// 先看之前分配为的考场里面能不能进去
int rnd = 0;// 表示id学生与第i个考场里面的人不认识的数量
for (int j = 1; j <= cnt[i]; ++j) // cnt[i]表示第i个考场里面的人数
if (e[id][vis[i][j]] == 0)rnd ++;
if (rnd == cnt[i]) { // 如果都不认识
vis[i][++cnt[i]] = id;
dfs(id + 1, num);
cnt[i]--;// 回溯
}
}
// 现有考场都不行,就要增加考场
vis[num + 1][++cnt[num + 1]] = id;
dfs(id + 1, num + 1);
--cnt[num + 1]; // 回溯
}
void solve() {
cin >> n >> m;
while (m--) {
int u, v;
cin >> u >> v;
e[u][v] = e[v][u] = 1;
}
dfs(1, 0);
cout << ans << "
";
}
6.合根植物
w星球的一个种植园,被分成 m * n 个小格子(东西方向m行,南北方向n列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
输入格式:
第一行,两个整数m,n,用空格分开,表示格子的行数、列数(1<m,n<1000)。
接下来一行,一个整数k,表示下面还有k行数据(0<k<100000)
接下来k行,第行两个整数a,b,表示编号为a的小格子和编号为b的小格子合根了。
格子的编号一行一行,从上到下,从左到右编号。
比如:5 * 4 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
样例输入:
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
样例输出:
5
其合根情况参考图[p1.png]
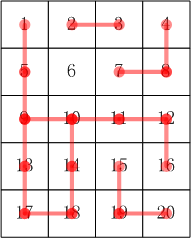
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 2000ms
待补