P6216 回文匹配 题解

题面

回文匹配

思路

前置知识

1. manacher 马拉车
2. kmp

O(n*n)

有了上面两种算法的支持，考虑暴力，对于每个奇回文串，暴力找字符串内包含的模式串

核心代码

for (i=1;i<=n;i++)
	{
		for (j=i-r[i]+1;j<=i+r[i]-m;j++)
		if(v[j]) 
		{
			ans=(ans+min(j-(i-r[i]+1)+1,i+r[i]-1-(j+m-1)+1));
		}
	} 
	//50pts TLE

O(n)

首先kmp记录每个模式串的左端点在文本串出现的位置在打上标记，v[i]=1

依旧枚举每个奇回文串，我们发现每个匹配的串处更靠近回文串哪边的端点，那这两个端点的距离就是这个位置的模式串对当前回文串的贡献

靠左边的贡献

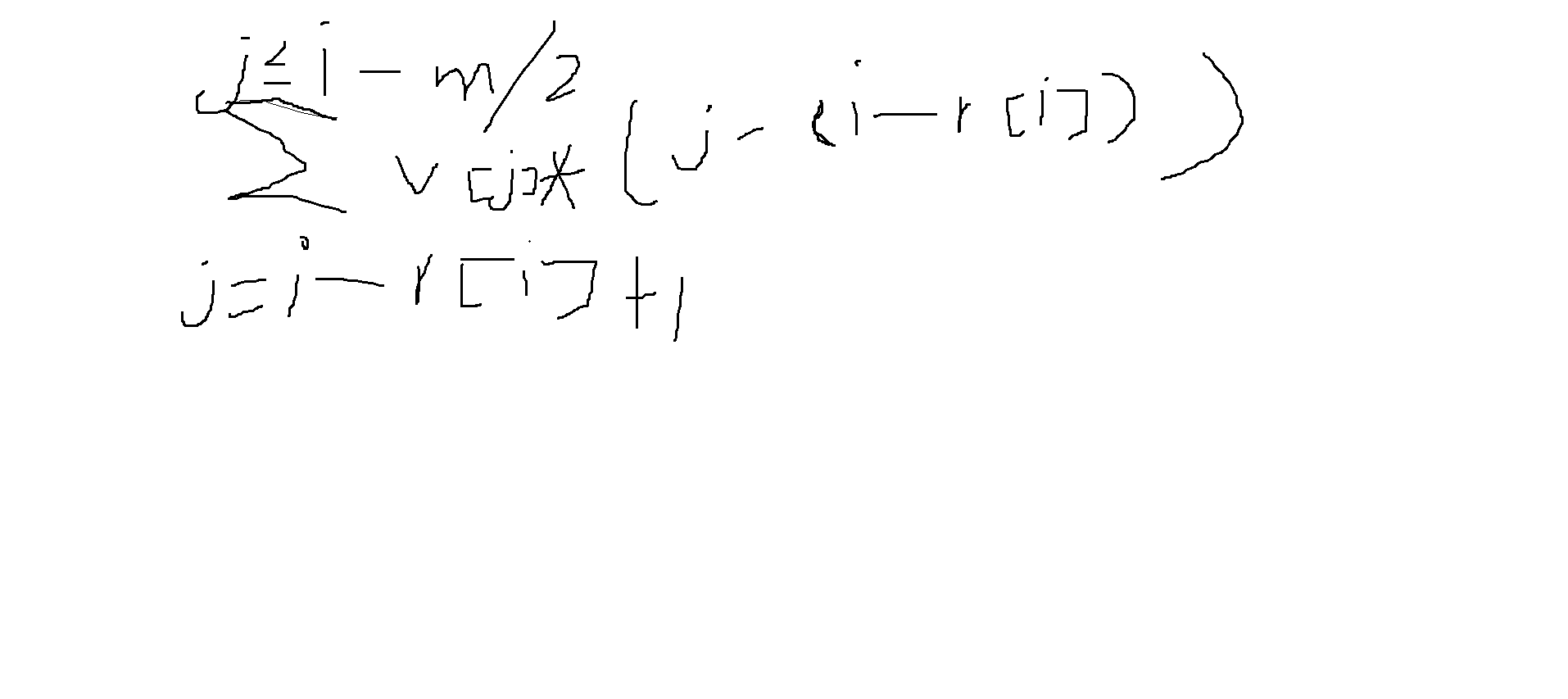
靠右边的贡献

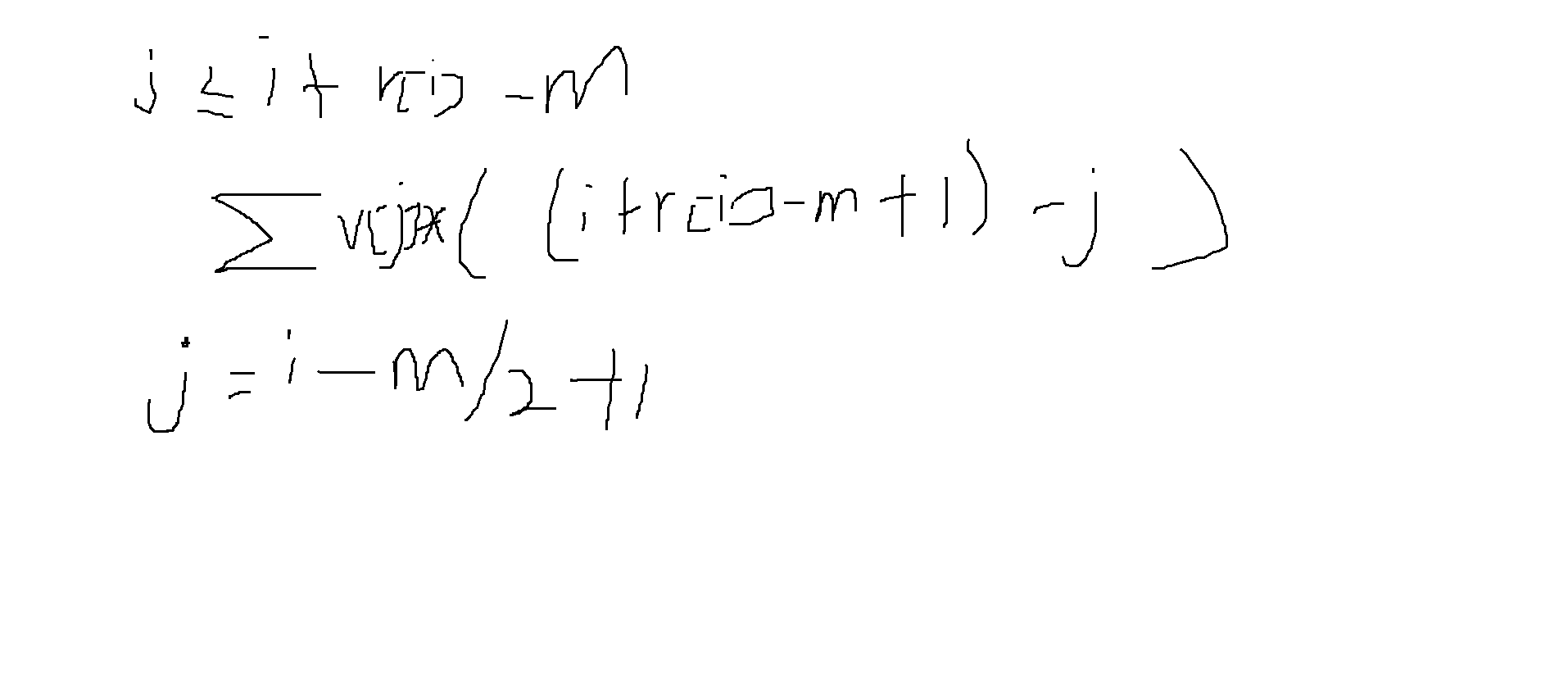
（以上j都是左端点）

把式子拆开，我们发现需要维护v[i]和v[i]*i的前缀和，再根据式子写出判定条件即可

容易出锅的细节p=2^32，千万不能(1<<32) ，应该(1ll<<32)

code

#include<bits/stdc++.h>
#define int long long
#define N 3000010
#define re register  
using namespace std;
int n,m,ans,kmp[N],r[N],v[N],pre[N],sum[N],p=(1ll<<32);
char a[N],b[N];
template <class T> inline void read(T &x)
{
	x=0;int g=1;char s=getchar();
	for (;s<'0'||s>'9';s=getchar()) if (s=='-') g=-1;
	for (;s>='0'&&s<='9';s=getchar()) x=(x<<1)+(x<<3)+(s^48);
	x*=g;
}
void kp()
{
	int i,j=0;
	for (i=2;i<=m;i++)
	{
		while(j&&b[i]!=b[j+1]) j=kmp[j];
		if (b[i]==b[j+1])j++;
		kmp[i]=j;
	} 
	j=0;
	for (i=1;i<=n;i++)
	{
		while(j&&a[i]!=b[j+1]) j=kmp[j];
		if (a[i]==b[j+1]) j++;
		if (j==m)	v[i-m+1]=1,j=kmp[j];
	}
}
void manacher()
{
	a[0]='#';int p=1,mx=1,i;
	for (i=1;i<=n;i++)
	{
		if (mx<=p) r[i]=1;
		else r[i]=min(mx-i,r[2*p-i]);
		while(a[i+r[i]]==a[i-r[i]]) r[i]++;
		if (i+r[i]>mx)	mx=i+r[i],p=i;
	}
}
signed main()
{
	re int i,j,x,y,z,op;
	read(n);read(m);
	scanf("%s",a+1);scanf("%s",b+1);a[n+1]=0;b[m+1]=0;
	kp();manacher();
	for (i=1;i<=n;i++) sum[i]=sum[i-1]+v[i];
	for (i=1;i<=n;i++) pre[i]=pre[i-1]+v[i]*i;
	for (i=1;i<=n;i++) 
	{
		if (m>2*r[i]-1) continue;
		if (i-m/2>i-r[i]) ans+=pre[i-m/2]-pre[i-r[i]]-(i-r[i])*(sum[i-m/2]-sum[i-r[i]]);ans%=p;
		if (i+r[i]-m>i-m/2) ans+=(i+r[i]-m+1)*(sum[i+r[i]-m]-sum[i-m/2])-(pre[i+r[i]-m]-pre[i-m/2]);ans%=p;
	}
	printf("%lld
",ans); 
	return 0;
}