斜率DP
斜率DP的一版模式:给你一个序列,至多或分成m段,每段有花费和限制,问符合情况的最小花费是多少;
一版都用到sum[],所以符合单调,然后就可以用斜率优化了,很模板的东西;
如果看不懂可以先去看一下本博客----斜率DP题目,看一下第一道题目,然后在回来看push,pop是为什么这样操作;
首先通过对方程的化简得到如下递推方程
DP[i] = min/max( -a[i]*x[j] + y[j] ) + w[i]; (1<=j<i)
一般情况下,x[j],y[j],a[i]都是单调递增的,(求最小值,维护的是下右凸包)
当然也可以x[j]单调递减,y[j]单调递增,a[i]单调递增;(求最小值,维护的是下左凸包)
对于DP[i],显然只要找到一个j使a[i]*x[j]+y[j]最小就可以了,
注意对于DP[i]来说,a[i],w[i]都是常量;
一般对于DP[i] =min/max(-a[i]*x[j] + y[j] )+ w[i],最朴素的时间复杂度是O(n^2);
为什么可以优化呢
设G = -a[i]*x[j] + y[j],
移项: y[j] = a[i]*x[j] + G;
现在的问题就是:已知道a[i]也就是斜率,给你几个点(x[j],y[j]),找一个点带入使得G最小;
G是直线与Y轴的交点的纵坐标的值,显然这个点一定在这些点形成的凸包上,
(图是x[i],y[i],单调递增,斜率为正的情况)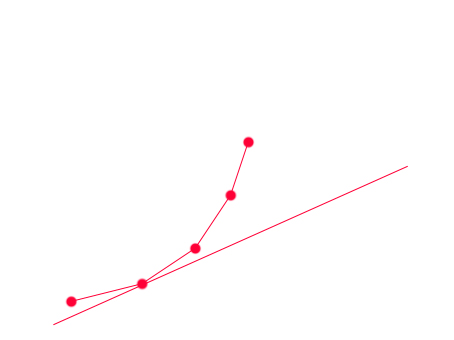
因为我们在从小到大递推求解,求DP[i]的时候DP[j](0<=j<i)都是已知的
所以我们可以在求完DP[i]之后可以马上把点(x[i],y[i])加入,来维护一个凸包;
这里还需要一个小知识点,就是凸包的维护,如果写过凸包的话,我们都知道在维护前
都要先把点排序(不管是水平序,还是极角序)
这就是为什么要x[i],y[i]是单调的原因了,只有单调才可以按照递推的顺序直接维护凸包了;
但如果所有的点都在凸包上,那么这个优化也就不算优化了,
所以问题变成:
对于一条已知斜率的直线,如何从凸包上找一个点使它与Y轴的交点的纵坐标值最小;
对于一个下凸包,且斜率单调递增:(求最小值的情况下)
我们现在假设直线和下凸包里斜率最小的直线重合,不断的变大这条直线的斜率,
也就是沿着这个凸包旋转,
我们发现,这条直线要么跟凸包的一条直线重合,要么经过凸包的一个点,
且一旦一个点被旋转过去后,接下来斜率变大的直线都不可会再经过这个点重合,
也就是说一旦一个点被淘汰了,那么它在接下来的过程中也不会被用到,
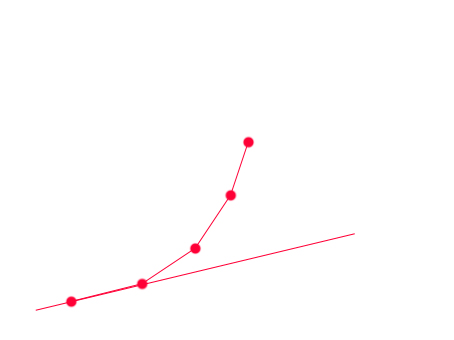
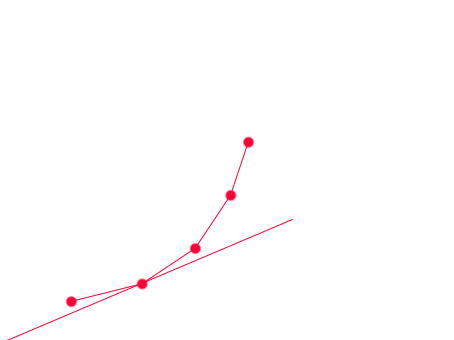
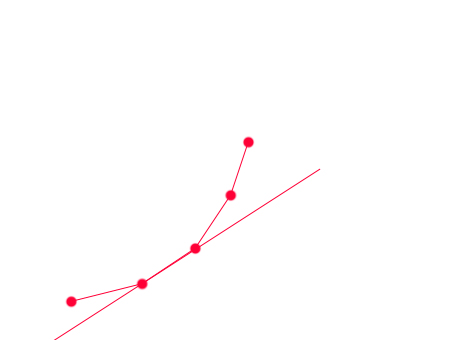
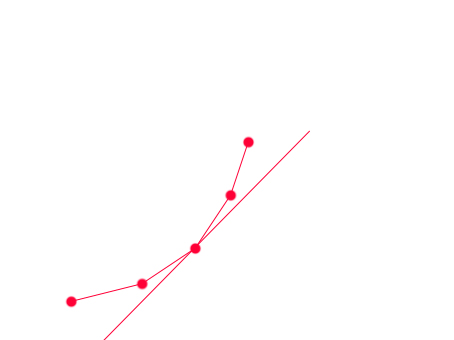

这样我们就有一个O(n)的算法,每次从凸包队列里从头比较相临的俩个点,谁得到的G
比较小,如果后一个点得到的G小,说明前一个点在接下来的状况下也不是最优的,所以
可以直接淘汰。
而所谓的单调队列优化其实也是这样,就是在队列里维护可能提供最优值的那些状态,
不断的插入新的点,不断的删掉不符合或者不优的点;
然后在维护的队列里快速的找到那个使当前状态最优的那个状态;
1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<iostream> 5 #include<algorithm> 6 #include<cmath> 7 #include<vector> 8 #include<set> 9 using namespace std; 10 const int N=50000+10; 11 typedef long long LL; 12 struct Point{ 13 LL x,y;
15 Point (LL a=0,LL b=0):x(a),y(b){} 16 Point operator - (const Point &p) const{ 17 return Point(x-p.x,y-p.y); 18 } 19 }; 20 typedef Point Vector; 21 inline LL Cross(const Vector &u,const Vector &v){ 22 return u.x*v.y - u.y*v.x; 23 } 24 int n,M; 25 struct dequeue{ 26 Point q[N]; 27 int head,tail; 28 void init(){ 29 head = 1; tail = 0; 30 } 31 void push(const Point &u){ 32 while (head < tail && Cross(q[tail]-q[tail-1],u-q[tail-1]) <= 0 ) tail--; 33 q[++tail] = u; 34 } 35 Point pop(const LL &k){//斜率的大小 36 while (head < tail && k*q[head].x + q[head].y >= k*q[head+1].x + q[head+1].y ) head++; 37 return q[head]; 38 } 39 }H; 40 // dp[i] = -k*x[j] + y[j] + w; 41 // 写成结构体常数比较大; 42 void solve(){ 43 44 H.init(); 45 //队列里初始值得看情况,比如H.push(Point(0,0)); 46 for (int i=1;i<=n;i++){ 47 Point t = H.pop(k); 48 dp[i] = -k*t.x + t.y + W; 49 H.push(Point(x[i],y[i])); 50 } 51 }
还有就是不满足单调的,首先是
斜率不满足单调性,x[i],y[i]还是满足单调;
这样凸包还是可以直接维护的,但是找凸包上的点就不能在o(1)的时间找到;
但是我们可以用三分找,因为按照队列里点的顺序G值是先变小后变大的;
也可以二分斜率,因为在凸包上相邻两个点的斜率是单调递增的;

1 用find()代替pop(); 2 int find(const LL &k){ 3 int l = head, r = tail; 4 while (r - l >= 3){ 5 int m1 = l + (r-l)/3; 6 int m2 = r - (r-l)/3; 7 if (k*q[m1].x+q[m1].y >= k*q[m2].x+q[m2].y ) l = m1+1; 8 else r = m2-1; 9 } 10 int ret = l; 11 for (int i = l+1; i <= r; i++) { 12 if (k*q[i].x+q[i].y <= k*q[ret].x+q[ret].y) ret = i; 13 } 14 return ret; 15 }
然后如果x[i],y[i]也不满足单调,这样就不能直接维护凸包了,需要动态维护凸包
简单点的就是用set,但是set无法实现kth大,所以得自己写平衡树;
先找到插入点前驱,和后继(水平序),然后分两边同时维护凸包,(如果还不太清楚可以看一下本博客的动态凸包的代码)
再用三分找最小;
要用到的就是findPre(),findNext(),kth();当然也可以在插入的时候记录下该点跟前驱的斜率,然后
直接查找第一个比读入斜率大的点就可以,因为在平衡树里斜率也是满足二叉树的性质的,这样就不用kth()了,
代码可以参看hust里;
因为一个点被删除后就不会在进入凸包,时间O(logn),查找要logn;
所以总时间复杂度为O(logn*logn*n);
http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=31649
货币兑换:splay dp[i] = ai[i]*x[j]+bi[i]*y[j] -----> dp[i]/bi[i] = ai[i]/bi[i] *x[j] +y[j];

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<cmath> 6 #include<vector> 7 #include<cstdlib> 8 using namespace std; 9 const int N=100000+10; 10 const double eps=1e-8; 11 inline int dcmp(double x){ 12 return x<-eps ? -1 : x>eps; 13 } 14 struct Point{ 15 double x,y; 16 Point(double a=0,double b=0):x(a),y(b){} 17 Point operator - (const Point &p)const{ 18 return Point(x-p.x,y-p.y); 19 } 20 double operator * (const Point &p)const{ 21 return x*p.y - y*p.x; 22 } 23 bool operator < (const Point &p)const{ 24 return dcmp(x-p.x)<0 || (dcmp(x-p.x)==0 && dcmp(y-p.y)<0); 25 } 26 }; 27 struct splay_tree{ 28 int sz,root,ch[N][2],pre[N],ss[N]; 29 Point val[N]; 30 void rotate(int x){ 31 int y = pre[x]; 32 int f = (ch[y][0]==x); 33 ch[y][f^1] = ch[x][f]; 34 pre[ ch[x][f] ] = y; 35 pre[ x ] = pre[ y ]; 36 ch[ pre[y] ][ ch[ pre[y] ][ 1 ] == y ] = x; 37 ch[x][f] = y; 38 pre[y] = x; 39 pushup(y); 40 } 41 void splay(int x,int goal){ 42 while (pre[x] != goal ){ 43 int y = pre[x], z = pre[y]; 44 if (z==goal){ 45 rotate(x); 46 }else { 47 int f = (ch[z][0]==y); 48 if (ch[y][f] == x){ 49 rotate(x); rotate(x); 50 }else { 51 rotate(y); rotate(x); 52 } 53 } 54 } 55 pushup(x); 56 if (goal == 0) root=x; 57 } 58 void init(){ 59 sz=0; ch[0][0]=ch[0][1]=pre[0]=0; val[0]=Point(0,0); ss[0]=0; 60 } 61 void pushup(int x){ 62 ss[x] = ss[ ch[x][0] ] + ss[ ch[x][1] ] + 1; 63 } 64 void insert(Point x){ 65 val[++sz]=x; ss[sz]=1; 66 ch[sz][0]=ch[sz][1]=pre[sz]=0; 67 if (sz==1){ 68 root=1; return; 69 } 70 int u,f; 71 for (u=root; ch[u][f=val[u]<x]; u=ch[u][f]); 72 ch[u][f] = sz; 73 pre[sz] = u; 74 splay(sz,0); 75 if (sz<=2) return; 76 ins(sz); 77 } 78 void remove(int x){ 79 int u = findPre(x), v = findNext(x); 80 splay(u,0); splay(v,u); 81 ch[v][0]=0; 82 splay(v,0); 83 } 84 int findPre(int x){ 85 splay(x,0); 86 int u; 87 if (ch[x][0]==0) return 0; 88 for (u=ch[x][0]; ch[u][1]; u=ch[u][1]); 89 return u; 90 } 91 int findNext(int x){ 92 splay(x,0); 93 int u; 94 if (ch[x][1]==0) return 0; 95 for (u=ch[x][1]; ch[u][0]; u=ch[u][0]); 96 return u; 97 } 98 void ins(int x){ 99 int u = findPre(x), v = findNext(x); 100 if (u!=0 && v!=0) { 101 double k= (val[u]-val[x])*(val[v]-val[x]); 102 if (dcmp(k)<=0) { 103 remove(x); return; 104 } 105 } 106 while (1){ 107 u=findNext(x); 108 if (u==0) break; 109 v=findNext(u); 110 if (v==0) break; 111 double k=(val[u]-val[x])*(val[v]-val[x]); 112 if (dcmp(k)>=0){ 113 remove(u); 114 }else break; 115 } 116 while (1){ 117 u=findPre(x); 118 if (u==0) break; 119 v=findPre(u); 120 if (v==0) break; 121 double k=(val[u]-val[x])*(val[v]-val[x]); 122 if (dcmp(k)<=0){ 123 124 remove(u); 125 }else break; 126 } 127 } 128 int kth(int k){ 129 int tmp=k; 130 if (k>ss[root]) return 0; 131 int x = root; 132 while (ss[ ch[x][0] ]+1!=k){ 133 int c = ss[ ch[x][0] ]; 134 if (k<=c) x = ch[x][0]; 135 else { 136 x = ch[x][1]; 137 k -= c+1; 138 } 139 } 140 splay(x,0); 141 return x; 142 } 143 double cal(double k,int x){ 144 return k*val[x].x+val[x].y; 145 } 146 Point find(double k){ 147 int l=1,r=ss[root]; 148 while (r-l>3){ 149 int m1= l+(r-l)/3; 150 int m2= r-(r-l)/3; 151 if (cal(k,kth(m1))>cal(k,kth(m2))) r=m2-1; 152 else l=m1+1; 153 } 154 int ret=kth(l); 155 double tmp=cal(k,ret); 156 for (int i=l+1;i<=r;i++){ 157 int t=kth(i); 158 double t2=cal(k,t); 159 if (tmp<t2) { 160 ret=t; tmp=t2; 161 } 162 } 163 return val[ret]; 164 } 165 void debug(){ 166 printf("root: %d ",root);print_tree(root); 167 } 168 void print_tree(int x){ 169 if (x){ 170 print_tree(ch[x][0]); 171 printf("now: %d ,fa: %d ,son0: %d ,son1: %d ,size: %d ",x,pre[x],ch[x][0],ch[x][1],ss[x]); 172 print_tree(ch[x][1]); 173 } 174 175 } 176 }H; 177 int n,s; 178 double ak[N],bk[N],rk[N]; 179 double dp[N]; 180 void solve(){ 181 H.init(); 182 double x,y; 183 dp[1]=s; 184 y = (double)s/(rk[1]*ak[1]+bk[1]); 185 x = rk[1]*y; 186 H.insert(Point(x,y)); 187 for (int i=2;i<=n;i++){ 188 Point t = H.find(ak[i]/bk[i]); 189 dp[i] =max(dp[i-1], ak[i]*t.x+bk[i]*t.y); 190 y = dp[i]/(rk[i]*ak[i]+bk[i]); 191 x = rk[i]*y; 192 H.insert(Point(x,y)); 193 } 194 printf("%.3lf ",dp[n]); 195 } 196 int main(){ 197 // freopen("in.txt","r",stdin); 198 // freopen("1.out","w",stdout); 199 while (~scanf("%d%d",&n,&s)){ 200 for (int i=1;i<=n;i++) scanf("%lf%lf%lf",&ak[i],&bk[i],&rk[i]); 201 solve(); 202 } 203 204 return 0; 205 }
这样对于形如 DP[i] = min/max(-a[i]*x[j]+y[j])+w[i]; (1<=j<i)
的DP方程都可以解决了;
