算法拾遗-简单算法的伪码实现

　　看了算法设计相关的书，写伪码是算法设计的基本功。解决一个问题，看似最终是用具体的编程语言实现的，但是用伪码最能表现其思想，好的伪码，可以把问题阐述的非常简单清楚,代码就水到渠成了。比如插入排序算法，我们可以写一个c++实现算法，但是用一个伪码更能体现出其过程。

　　辗转相除法求最大公约数：

//用来递归，思想很简单，同时写法上没有定义gcd函数的返回值
gcd(small,big):
    r = big % small;
    if (r == 0)
          return small;
    return gcd(r,small);

　　

　　一个最简单的求无序列表最大值的伪码：

// 求列表最大值得伪码,越简单越清晰越好
a1,a2... an;
max =a1;
for i= 2 to n
    if ai>max then
        set max = ai
return max

　　在尝试些一个插入排序：

a1,a2,a3...an
//这就是复杂一些，但是伪码看还是很清晰的,也容易发现错误
for i=2 to n
    for j = 1 to (i-1)
        if ai < aj then 
            set temp = ai
            for k = j to i then 
                 ak+1 = ak
            set aj = ai;

　　这个算法是否和求（a,b)直接的素数相似呢？不相似，虽然都对范围内的数进行了处理

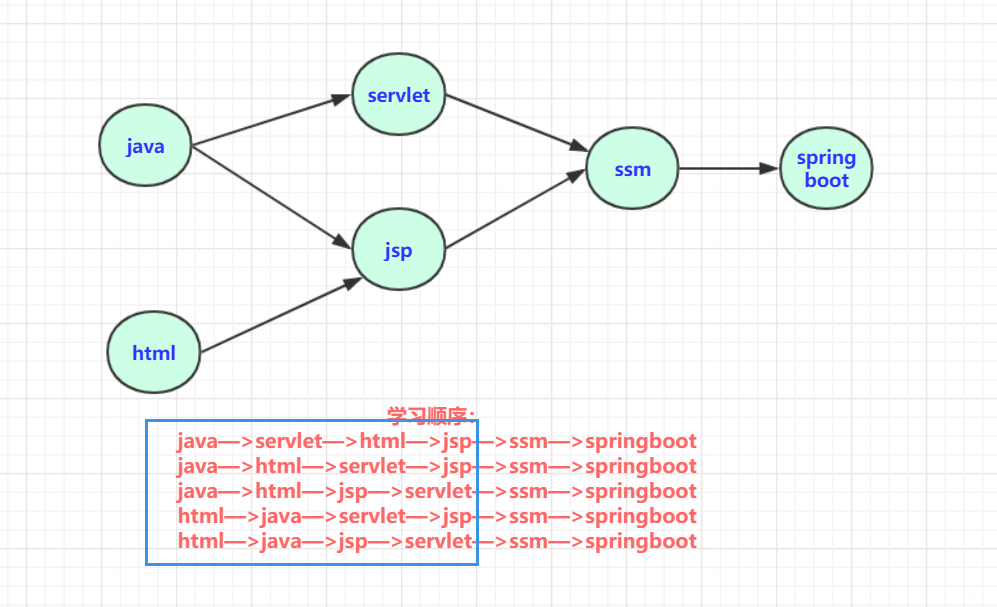
　　拓扑排序的问题只对有向图有效，并且引入出度和入度的概念，就非常好理解了。如果凭空去寻节点的前项节点，真的不好搜寻，这个算法还是很奇特的。主要有两个步骤，1.在图中查找入度为零的节点，2.将这些节点删掉，并删除路径，然后继续循环。

 

topologicalOrder(G(V,E)):
    intialize the result list;
    while G is not null
        for all node in G:
            find the nodes with no incoming edge
            add the nodes in list
　　　　　　　//这个过程中，G是在不断的改变的。
            remove the nodes from G,remove the related edges

参考资料：https://cloud.tencent.com/developer/article/1383822

参考资料：https://www.cnblogs.com/bigsai/p/11489260.html