Description

题解
(这可是一道很早就碰到的练习题然后我不会做不想做,没想到在Contest碰到欲哭无泪......)
题目大意是寻找三点对的个数,使得其中的三个点两两距离都为d。
问题在于,这个d不是定值啊,这使得DP的进行比较困难。
于是这个神奇解法在DP过程中把d省去了!
状态表示
$f [u][i]$: 以u为根的子树内,到u的距离为i的节点个数,$f [u][0]=1$ 。
$g [u][i]$:以u为根的子树内,存在多少点对 (a,b),它们到它们的lca的距离都为d,且它们的lca到u的距离恰好为d-i。
Wait?What? 为什么出现了d?为什么是d-i?d不是一个不确定的值吗?g是个什么鬼?
(额看图看图,f应该很容易懂吧,我们现在来弄懂g)
g的示意图:
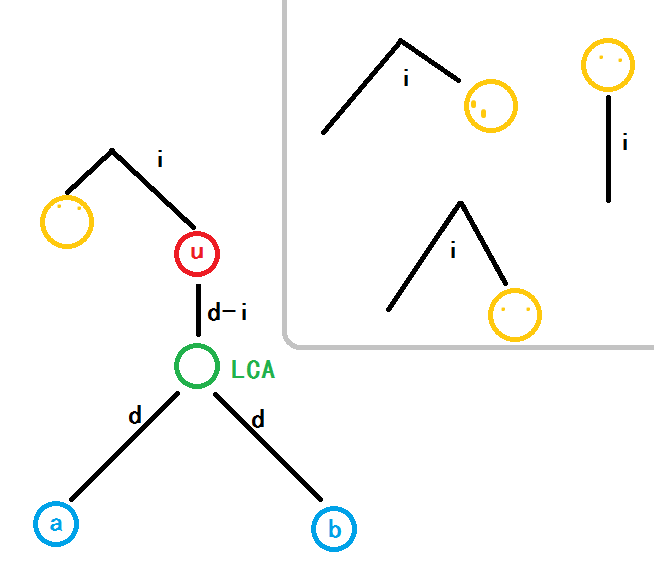
可以发现,三点对中,a和b这两个点已经确定,到LCA的长度都为d;而u到LCA这段要记录为d-i,实际上代表的是,u上面还要接一段长度为i的链 (d-i+i=d),才能组成一个合法的三点对(a,b,和小黄点)。上图右框中都是符合的链,都可以接到u的上方,组成所求的三点对。
但是,d是不是还隐约存在于我们的定义之中呢......再看一幅图,实际上d是完全不存在的:
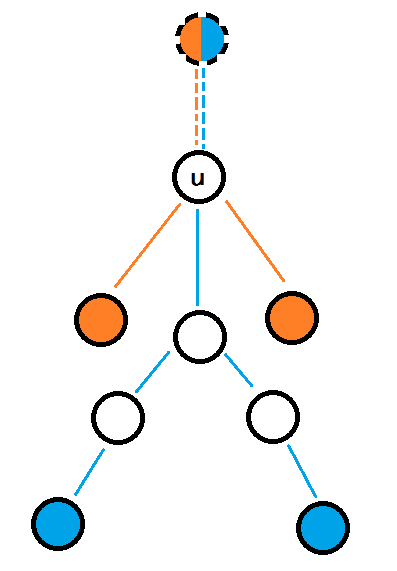
对于u这个点,$g [u][1]=2$,即满足$ g[u][1]$的点对数量为2。 因为不论是橙色的两个点还是蓝色的两个点,它们都可以通过在u上面连一条长为1的链,与链的另一端的节点组成完整的三点对。d不同的三点对,同样也能被记录入同一种状态。
于是我们就发现,g的定义完美地将最不稳定的因素d给省去了!
(搞定g是一个比较关键的步骤)
状态转移
现在我们看回f和g,稍加观察可以得出状态转移方程。
对于根节点为u的子树,记v为u的某一个儿子。我们先用当前u子树的统计信息与v的信息进行统计更新答案,随后将v合并入u子树的统计信息中。
- $Ans += Sigma g [u][i]*f [v][i-1] + Sigma g [v][i]*f [u][i-1]$
- $g [u][i] += g [v][i+1] + f [u][i]*f [v][i-1] $
- $f [u][i] += f [v][i-1]$
(以上的i-1或i+1,通过画图可以理解出来)
实现上,先递归儿子,返回时再更新与合并。
一定要注意边界问题!每个转移最好分开循环,以应对不同边界。(实在想不出请看代码)
时空复杂度$O(n^2)$
啥?
优化
我们采用长链剖分来优化转移。
考虑对于一个以u为根的子树,如果u只有一个儿子v,我们要怎么转移呢?
很显然很简单:
- $f [u][i]=f [v][i-1]$
- $g [u][i]=g [v][i+1]$
对于u的重儿子v,我们采用此方法直接通过指针O(1)转移;对于u的轻儿子(其他儿子),我们采用上方描述的方法进行暴力转移。
这样我们的时间复杂度就由$O(n^2)$降为了$O(n)$
空间呢?指针转移呢?
存储方式
按说刚刚提到重儿子v直接$O(1)$转移的方式是指针,是因为我们发现有大量重复元素。对于一条重链上每个节点的f,我们发现父亲总是包含重儿子的信息;对于每个节点的g,我们发现重儿子的数组总是父亲数组向左偏移一位。
现在,我们将$f [i][j]$映射到一维数组上(具体实现可以通过一个函数搞定,详细见代码的f(x,y)与g(x,y),真正的一维数组是F和G)
对于一条重链,若长度为len,那么我们可以只为这条重链申请长度为len的f数组空间,以及长度为2*len的g数组空间(因为每个节点的g数组都有len的大小,每次往左移动一位,最多移动len次)。这样f数组最大只会用到n,g数组最大只会用到2n,我们将空间复杂度降到了$O(n)$。

现在我们优先递归重儿子,从重儿子回溯后,就已经自动计算好了重儿子的答案啦,下面按照上面方法暴力合并其他子树即可。
特别地:从重儿子回溯的时候,需将$Ans+=g [u][0]$($g [u][0]$即$g [重儿子][1]$),因为回溯的时候u充当了一个上端点,能与$g [重儿子][1]$组成答案(其实还不是全自动,是半自动......)。而从其他子树回溯的时候,上述状态转移方程可以覆盖这种情况。
总时间复杂度O(n),空间复杂度O(n)。

1 #include <bits/stdc++.h> 2 typedef long long ll; 3 using namespace std; 4 const int N=50010; 5 int n,tot,h[N]; 6 int dep[N],maxdep[N],son[N],top[N],stF[N],stG[N],posF,posG; 7 ll F[N],G[N*2],ans; 8 struct Edge{int v,next;}eg[N*2]; 9 inline void addEdge(int u,int v){ 10 eg[++tot].v=v; eg[tot].next=h[u]; h[u]=tot; 11 } 12 void preDfs(int u,int fa,int deep){ 13 dep[u]=maxdep[u]=deep; 14 son[u]=-1; 15 for(int i=h[u],v;i;i=eg[i].next) 16 if((v=eg[i].v)!=fa){ 17 preDfs(v,u,deep+1); 18 maxdep[u]=max(maxdep[u],maxdep[v]); 19 if(son[u]==-1||maxdep[v]>maxdep[son[u]]) 20 son[u]=v; 21 } 22 } 23 inline int f(int x,int y){return stF[top[x]]+dep[x]-dep[top[x]]+y;} 24 inline int g(int x,int y){return stG[top[x]]-(dep[x]-dep[top[x]])+y;} 25 inline int De(int u){return maxdep[u]-dep[u]+1;} 26 void dfs(int u,int fa,int Top){ 27 top[u]=Top; 28 if(u==Top){ 29 stF[u]=posF; 30 posF+=De(u); 31 posG+=De(u)*2; 32 stG[u]=posG-De(u); 33 } 34 if(son[u]==-1) return; 35 dfs(son[u],u,Top); 36 for(int i=h[u],v;i;i=eg[i].next) 37 if((v=eg[i].v)!=fa&&v!=son[u]) 38 dfs(v,u,v); 39 } 40 void count(int u,int fa){ 41 F[f(u,0)]=1; 42 if(son[u]!=-1){ 43 count(son[u],u); 44 ans+=G[g(u,0)]; 45 } 46 for(int I=h[u],v;I;I=eg[I].next){ 47 if((v=eg[I].v)!=fa&&v!=son[u]){ 48 count(v,u); 49 for(int i=1;i<=De(v);i++) 50 ans+=G[g(u,i)]*F[f(v,i-1)]; 51 for(int i=1;i<De(v);i++) 52 ans+=G[g(v,i)]*F[f(u,i-1)]; 53 for(int i=1;i<=De(v);i++) 54 G[g(u,i)]+=F[f(u,i)]*F[f(v,i-1)]; 55 for(int i=0;i<=De(v)-2;i++) 56 G[g(u,i)]+=G[g(v,i+1)]; 57 for(int i=1;i<=De(v);i++) 58 F[f(u,i)]+=F[f(v,i-1)]; 59 } 60 } 61 } 62 inline void init(){ 63 tot=posF=posG=ans=0; 64 memset(h,0,sizeof h); 65 memset(F,0,sizeof F); 66 memset(G,0,sizeof G); 67 } 68 int main(){ 69 while(1){ 70 scanf("%d",&n); 71 if(!n) break; 72 init(); 73 for(int i=1,x,y;i<n;i++) 74 scanf("%d%d",&x,&y), 75 addEdge(x,y), addEdge(y,x); 76 preDfs(1,0,1); 77 dfs(1,0,1); 78 count(1,0); 79 printf("%lld ",ans); 80 } 81 return 0; 82 }
