Time Limit: 1000 ms Memory Limit: 256 MB
Description

题解
状态表示:
这题的状态表示有点难想......
设$f_i$表示第$i$个事件经过之后,到达终点之前,不再回到事件$i$或事件$i$的左边的概率,反过来说就是可以在右边乱绕,若事件$i$的位置为pos,“右边”指的就是$(pos,h]$。
我们将第$i$个事件到第$i+1$个事件中间这一段路程记为$S_i$,那么期望经过$S_i$的次数就为$1/f_i$。
为什么是$1/f_i$呢?具体来说,只在右边乱绕,最左也只能到达$i+1$;一旦跨越到i或i的左边位置,那么S就必须要被经过了。所以$f_i$越小,被踢到左边或起点的概率就越大,经过$S_i$的概率和期望也就越大。
Orzhy Orzyww Orzyxq
状态转移:
我们采用反向转移。
考虑$f_i$,我们应该从$f_i+1$得到。
我们令$p_i$为第$i$个事件的成功概率(获得Flag或打败敌人的概率)。
- 如果$i+1$个事件是一个敌人,那么
$f_i=f_{i+1}*p_{i+1}$
- 如果$i+1$个事件是一面FLAG,那么
$f_i=f_{i+1}+(1-f_{i+1})*p_{i+1}*f_{i+1}+((1-f_{i+1})*p_{i+1})^2*f_{i+1}+...+((1-f_{i+1})*p_{i+1})^k*f_{i+1}$
$=f_{i+1}*(1+p_{i+1}*(1-f_{i+1})+p_{i+1}^2*(1-f_{i+1})^2+...+p_{i+1}^k*(1-f_{i+1})^k)$
${k oinfty}$
可以运用极限等式的求法可以将极限部分转换为下式的分母:
$f_i=frac{f_{i+1}}{(1-p_{i+1}*(1-f_{i+1}))}$
这是什么意思呢?
看回第一个式子,$(1-f_{i+1})$的意思是被弹回i+1或i+1的左边,$p_{i+1}$的意思是被$i+1$这个旗子留住,$f_{i+1}$的意思是从$i+1$一路走到终点的概率。
$(1-f_{i+1})*p_{i+1}*f_{i+1}$意思是按下图的1-2-3顺序执行
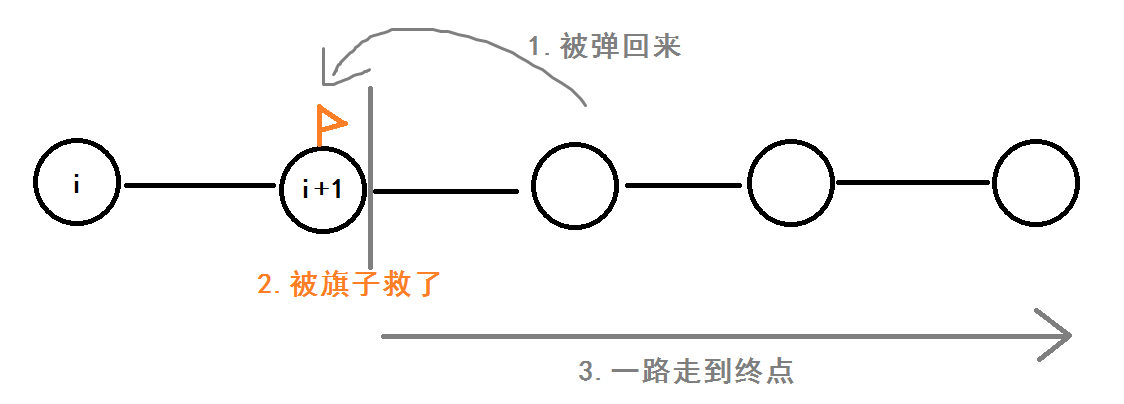
同理,$((1-f_{i+1})*p_{i+1})^2*f_{i+1}$表示1-2-1-2-3,$((1-f_{i+1})*p_{i+1})^3*f_{i+1}$表示1-2-1-2-1-2-3,以此类推即可。
计算时所有除法转为逆元,记得%多一点(记8.17)