Description
Special Judge

Hint
注意是全程不能经过两个相同的景点,并且一天的开始和结束不能用同样的交通方式。
题解
题目大意:给定两组点,每组有$n$个点,有若干条跨组的有色无向边。求一种方案,包括若干个不相交的连通块,覆盖全部点,每个连通块满足能一笔画(不经过重复的点)并且相邻两次经过的边颜色不相同(开头和结尾经过的边也不能相同)。
是不是有点类似二分图匹配的问题呢?我们还是考虑用最大流来建图。
一笔画的时候,每一个经过的点有且只有一条入边,有且只有一条出边,即度数必须为2;两条边的颜色还不能相同。每一个点都如下图所示:
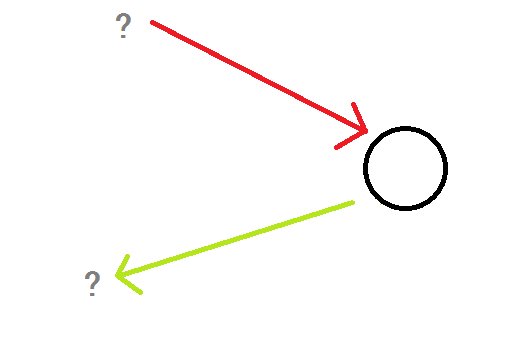
事实上,我们并不用考虑经过的每一条边的方向!这并不是我们决策的关键,只要最后回到起点即可,如下图所示。
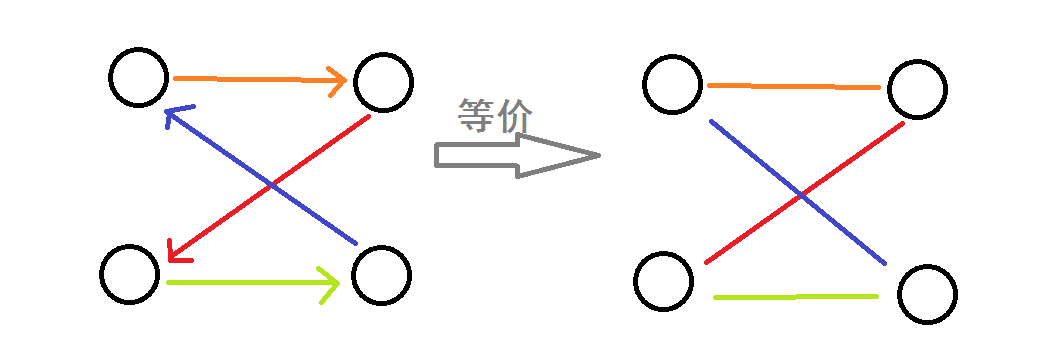
建图
怎么用最大流来限制这两个条件呢?
先上效果图:
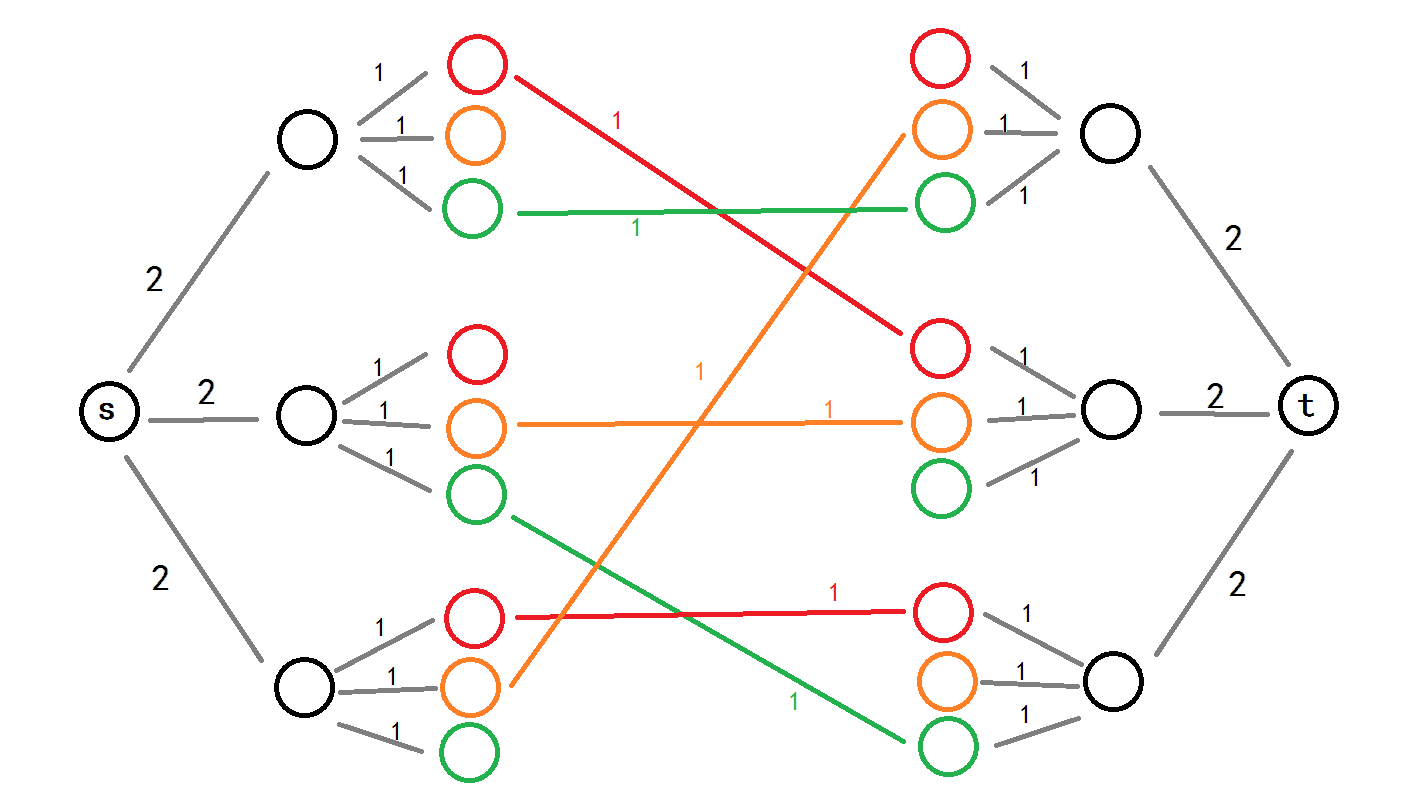
对于度数为2,考虑用一条容量为2的边限制。可以从源点向左边的每个点连接一条容量为2的边。
对于连到一个点的两条边的颜色不可以相同的限制,对于每一个点$u$新建$k$个点$u_1,u_2,...u_k$,并向它们连一条容量为1的边。这限制了每个点的每个颜色的出边至多只能有一条!
对于右边的点,我们镜像过去就好。
题目所连的边,我们按指定点的对应颜色,从左向右连接一条容量为1的边。
愉快地跑一次Dinic最大流。
由于题目保证一定有解,那么对于每一个连通块,块内所有点对应的2边一定是满流的。
也意味着,中间带颜色的边(即输入边),满流的就是答案经过的。
构造
现在我们只看答案经过的边,对于每个连通块直接模拟一笔画就好啦(随缘乱画),输出答案即可。
我的编号规则:
左边$n$个点:$[1,n]$
右边$n$个点:$(n,2n]$
每个点对应的$k$个颜色点:$(2n,2n+2nk]$。
源点:$2n+2nk+1$ 汇点:$2n+2nk+2$
(PS:这题的代码本来可以1A的然而输出的时候全部输出成最后一天了...天数和长度都对..看起来并没有什么不对...)

1 #include <cstdio> 2 #include <queue> 3 #include <cstring> 4 #include <vector> 5 using namespace std; 6 const int N=60,INF=2147000000; 7 int n,m,k,tot,h[700],S,T,ch[N*2][6],chcnt,rec[7000][3]; 8 int vis[700],dis[700],has[N*2]; 9 vector<int> lis[N*2],ans[N*2]; 10 struct Edge{int v,f,next;}g[7000]; 11 queue<int> q; 12 inline int addEdge(int u,int v,int f){ 13 g[++tot].v=v; g[tot].f=f; g[tot].next=h[u]; h[u]=tot; 14 g[++tot].v=u; g[tot].f=0; g[tot].next=h[v]; h[v]=tot; 15 return tot-1; 16 } 17 bool bfs(){ 18 memset(dis,-1,sizeof dis); 19 while(!q.empty()) q.pop(); 20 dis[S]=1; q.push(S); 21 int u,v; 22 while(!q.empty()){ 23 u=q.front(); q.pop(); 24 for(int i=h[u];i;i=g[i].next) 25 if(g[i].f&&dis[(v=g[i].v)]==-1){ 26 dis[v]=dis[u]+1; 27 q.push(v); 28 } 29 } 30 return dis[T]!=-1; 31 } 32 int dinic(int u,int delta){ 33 if(u==T) return delta; 34 int v,get,ret=0; 35 for(int i=h[u];i&δi=g[i].next) 36 if(g[i].f&&dis[(v=g[i].v)]==dis[u]+1){ 37 get=dinic(v,min(g[i].f,delta)); 38 g[i].f-=get; 39 g[i^1].f+=get; 40 delta-=get; 41 ret+=get; 42 } 43 if(!delta) dis[u]=-1; 44 return ret; 45 } 46 int main(){ 47 scanf("%d%d%d",&n,&m,&k); 48 tot=1; 49 S=n*2+n*2*k+1; T=S+1; 50 chcnt=n*2; 51 for(int i=1;i<=n*2;i++){ 52 if(i<=n) has[i]=addEdge(S,i,2); 53 else has[i]=addEdge(i,T,2); 54 for(int j=1;j<=k;j++){ 55 ch[i][j]=++chcnt; 56 if(i<=n) addEdge(i,ch[i][j],1); 57 else addEdge(ch[i][j],i,1); 58 } 59 } 60 for(int i=1,x,y,z;i<=m;i++){ 61 scanf("%d%d%d",&x,&y,&z); 62 rec[i][2]=addEdge(ch[x][z],ch[y+n][z],1); 63 rec[i][0]=x; rec[i][1]=y+n; 64 } 65 while(bfs()) 66 dinic(S,INF); 67 for(int i=1;i<=m;i++){ 68 int u=rec[i][0],v=rec[i][1],id=rec[i][2]; 69 if(!g[id].f&&!g[has[u]].f&&!g[has[v]].f){ 70 lis[u].push_back(v); 71 lis[v].push_back(u); 72 } 73 } 74 int day=0; 75 for(int i=1;i<=n;i++) 76 if(!vis[i]){ 77 vis[i]=1; 78 ans[++day].push_back(i); 79 for(int u=i,go=-1;go!=i;u=go){ 80 if(!vis[lis[u][0]]) go=lis[u][0]; 81 else if(!vis[lis[u][1]]) go=lis[u][1]; 82 else break; 83 vis[go]=1; 84 ans[day].push_back(go); 85 } 86 ans[day].push_back(i); 87 } 88 printf("%d ",day); 89 for(int i=1;i<=day;i++){ 90 int siz=ans[i].size(); 91 printf("%d ",siz); 92 for(int j=0;j<siz;j++) 93 if(ans[i][j]<=n) printf("L%d ",ans[i][j]); 94 else printf("R%d ",ans[i][j]-n); 95 puts(""); 96 } 97 return 0; 98 }
