Description
给定正整数(D),求有多少个正整数(N),满足(rev(N)=N+D)。
其中(rev(N))表示将(N)的十进制表示翻转来读得到的数(翻转后忽略前导零)。
答案对(10^9+7)取模。
(D le 10^{9})
(实际可以做到(D le 10^{5000}))
Solution
原题(D le 10^9),暴力可过;但DP做法可以应用到更大的范围。
考虑枚举(N)有多少位,记为(len)。
显然(len)不能小于(D)的位数,否则一定不合法。并且可以证明,(len)超过(D)的位数的两倍时,就没有数合法了。再者(len==1)的时候也显然不合法。所以枚举区间是([max (2,|D|),2|D|])。
设计一个DP来计算在(N)的长度为(len)时,有多少个数满足条件。
把和式画出来,并从两端向中间标号:
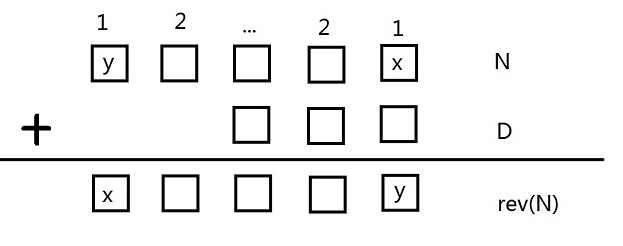
为什么要这么标号?因为既然是翻转,所以确定一组中的一对数((x,y))就可以确定另一对数((y,x))。
还要考虑进位问题,那么状态里应该有表示进位的东西。
设(f_{i,j,k})表示第(i)组数,其中左边一组数从其右边有无收到进位((j=0,1)),且右边一组数给其左边有无进位((k=0,1)):
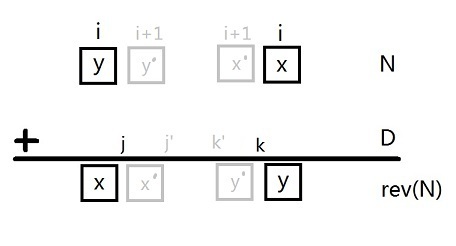
枚举状态(f_{i,j,k}),正向转移到可去的状态。枚举(i+1)组的(x')选0...9,并通过右边一组数的(k)和相应位置的(D)的数位算出(y'')与(k')。再用左边一组数的(j)来计算出(j')。如果(j'<0)或者(j'>1)就说明这个转移不合法,舍弃。因此,每个(x)的取值对应了唯一对应(有可能不合法,舍弃)的新状态(f_{i+1,j',k'}),将方案数加上即可。
注意第1组数的(x)不可以选0,不然会违背当前正在考虑长度为(len)的(N)这个前提。
如果(len)是偶数,那么对于(i=1..frac{len}{2})计算(f),答案即为(f_{frac{len}2,0,0}+f_{frac{len}2,1,1})
如果(len)是奇数,则先对于(i=1...lfloor frac{len}2
floor)计算(f),先枚举每个最终状态,再枚举最中间一位选择(0...9),是否能满足各个进位与否的要求,统计进答案即可。
总时间复杂度(mathcal O(frac{|D|^2}2*10*2*2)=mathcal O(|D|^220)),基本上不会跑满。我造数据时测了一下5000可以秒出,题目就开了5000的长度;然后我SUODCX后构造了一组特殊数据,使得(N)长度恰好是(2|D|)时也有解,几乎把复杂度卡满了,所以这个点只开到了3000(已经可以跑得出了).
Code
c++
#include <cstdio>
#include <cstring>
using namespace std;
const int N=10010,MOD=1e9+7;
int d[N];
int f[N][2][2];
inline int max(int x,int y){
return x>y?x:y;
}
void readData(){
static char str[N];
scanf("%s",str+1);
d[0]=strlen(str+1);
for(int i=1;i<=d[0];i++) d[d[0]-i+1]=str[i]-'0';
}
int dp(int n){
int m=n>>1;
for(int i=0;i<=m;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
f[i][j][k]=0;
f[0][0][0]=1;
for(int i=0;i<m;i++)
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
if(f[i][j][k]){
for(int x=0,y,j1,k1;x<10;x++){
k1=x+d[i+1]+k;
y=k1%10;
k1/=10;
j1=10*j+x-y-d[n-i];
if(j1<0||j1>1) continue;
if(!i&&(!x||!y)) continue;
(f[i+1][j1][k1]+=f[i][j][k])%=MOD;
}
}
int res=0;
if(n&1){
int mid=(n+1)>>1;
for(int j=0;j<2;j++)
for(int k=0;k<2;k++)
if(f[m][j][k])
for(int x=0,y;x<10;x++){
y=x+d[mid]+k;
if((x==y%10)&&(y/10==j))
(res+=f[m][j][k])%=MOD;
}
}
else{
for(int j=0;j<2;j++)
(res+=f[m][j][j])%=MOD;
}
return res;
}
void solve(){
int ans=0,maxlen=d[0]<<1;
for(int i=max(2,d[0]);i<=maxlen;i++)
(ans+=dp(i))%=MOD;
printf("%d
",ans<0?ans+MOD:ans);
}
int main(){
readData();
solve();
return 0;
}