无权二分图的最大匹配和完美匹配,以及用于求解匹配的匈牙利算法。
二分图:简单来说,如果图中点可以被分成2组,并且使得所有边都跨越组的边界,则这就是一个二分图。
准确的说:把一个图的顶点划分为2个不相交集U和V,使得每一条边都分别连接U,V中的顶点。如果存在这样的划分,则此图为一个二分图。
二分图的一个等价定义为:不含有 含奇数条边的环 的图。
图一是一个二分图,为了清晰,画成图二的形式。

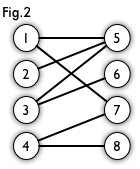
匹配:在图论中,一个匹配是一个边的集合,其中任意2条边都没有公共顶点,例如图3,图4红色的边就是图2的匹配。


我们定义匹配点,匹配边,未匹配点,未匹配边。图3中1,4,5,7为匹配点,其他未匹配;1-5 4-7匹配边,其他非匹配。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。