需要用线段树维护区间的3个变量:
区间最长的:[左连续前缀、右连续后缀、最大连续子区间] 的元素个数
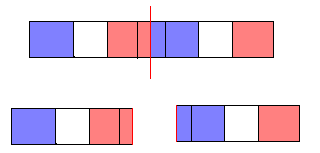
其中红线左侧的是第m个元素,右侧是m+1个元素。
更新完左右子树想要pushUp操作的时候,父亲的左前缀必然是左子的前缀,若是左子树满了,则左连续可能还要加上右子树的左前缀。同理,父亲的右后缀必然是右子的后缀,若是右子都连续,那么还要加上左子的后缀。
查询的时候,若是位置p在左子的“橙色“部分,即后缀中,那么结果应当是左子中的连续部分+(m+1)(即m的下一个元素)在右子的连续部分,同理p在右子的紫色部分时,要考虑加上左子的后缀部分。
代码:
#include <bits/stdc++.h> using namespace std; #define ll long long #define rep(i,a,b) for(ll i=(a);i<(b);++i) const int maxN = 5e4 + 5; int N, M, T; int stk[maxN]; #define lch rt << 1 #define rch rt << 1 | 1 #define lson l, m, rt << 1 #define rson m + 1, r, rt << 1 | 1 int lq[maxN << 2], rq[maxN << 2], aq[maxN << 2]; void pushUp(int l, int r, int rt) { int m = (l + r) / 2; lq[rt] = lq[lch]; rq[rt] = rq[rch]; int zy = max(lq[lch], rq[rch]); aq[rt] = max(zy, rq[lch] + lq[rch]); if (lq[lch] == m - l + 1) lq[rt] += lq[rch]; if (rq[rch] == r - m) rq[rt] += rq[lch]; } void init(int l, int r, int rt) { lq[rt] = rq[rt] = aq[rt] = r - l + 1; if (l == r) return; int m = (l + r) / 2; init(lson); init(rson); pushUp(l, r, rt); } void update(int p, int x, int l, int r, int rt) { if (l == r) { lq[rt] = rq[rt] = aq[rt] = x; return; } int m = (l + r) / 2; if (p <= m) update(p, x, lson); else update(p, x, rson); pushUp(l, r, rt); } int query(int p, int l, int r, int rt) { if (aq[rt] == r - l + 1 || aq[rt] == 0 || l == r) return aq[rt]; int m = (l + r) >> 1; if (p <= m) { if (p >= m - rq[lch] + 1) return query(p, lson) + lq[rch]; else return query(p, lson); } else { if (p <= m + lq[rch]) return query(p, rson) + rq[lch]; else return query(p, rson); } } int main() { // freopen("data.in", "r", stdin); while (~scanf("%d%d", &N, &M)) { char op[10]; int a, idx = 0; init(1, N, 1); rep(i, 0, M) { scanf("%s", op); if (op[0] == 'R') { update(stk[--idx], 1, 1, N, 1); continue; } scanf("%d", &a); if (op[0] == 'Q') { printf("%d ", query(a, 1, N, 1)); } else { update(a, 0, 1, N, 1); stk[idx++] = a; } } } return 0; }