今天也是考得西撇的一天。
CDQ就是怎么写都写不对 搞了将近两个小时 cnm听见没cnm
又开始出现时间不够 码力不足的问题了..
果然还是思维完全不行啊.....

这道题就是一个最大生成树的题 我之前从来都没有认真写过这个的题
或者是我写了然后忘了..
因为我们要求 i 到 j 所有路径经过点中最小值的最大值 所以考虑将点权从大到下排序
然后建造一棵最大生成树 因为是从大到小添加入连通块的
所以若是原来两个点没有联通 加上这个东西之后联通了
那么就说明这个点是这两者路径中最小值的最大值 然后就可以统计答案了
连接两个点他们所属于的连通块 两块中的点可以两两组合 那么路径就是两块的size之积再乘以点权
最后答案要×2 因为 算了f( i , j )和f( j , i )
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e6 + 5; int n,fa[N],m,head[N],tov[2 * N],nex[2 * N]; int tot,w[N],siz[N],nd[N]; ll ans; void add(int u,int v) { tot ++; nex[tot] = head[u]; head[u] = tot; tov[tot] = v; } bool cmp(const int & a,const int & b) { return w[a] > w[b]; } int find_fa(int x) { return x == fa[x] ? x : fa[x] = find_fa(fa[x]); } int read( ) { int ans = 0,t = 1; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } int main( ) { freopen("zoo.in","r",stdin); freopen("zoo.out","w",stdout); scanf("%d%d",& n,& m); for(int i = 1;i <= n;i ++) scanf("%d",& w[i]); for(int i = 1;i <= m;i ++) { int u,v; scanf("%d%d",& u,& v); add(u,v); add(v,u); } for(int i = 1;i <= n;i ++) { siz[i] = 1; fa[i] = i; nd[i] = i; } sort(nd + 1,nd + n + 1,cmp); for(int j = 1;j <= n;j ++) { int u = nd[j]; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; int uu = find_fa(u),vv = find_fa(v); if(w[v] < w[u] || uu == vv) continue; ans += 1LL * w[u] * siz[uu] * siz[vv]; fa[vv] = uu; siz[uu] += siz[vv]; } } printf("%I64d",ans * 2); }

这道题是可以用cdq的 我在考场上面就写得cdq 然而写挂了... 难受
然后正解要简单得多 就是树状数组 由题目可以知道覆盖区间的长度是递增的
那么对于一段区间[ a , b ] 画个图
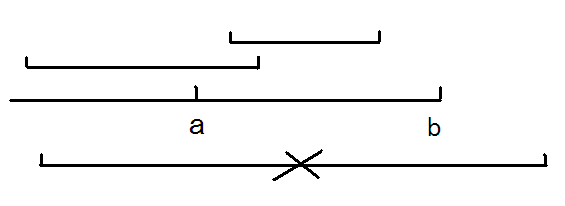
该区间能够完全覆盖的区间数 就是b向左的右端点数 - a向右的左端点数
a那边表示有多少区间不能被完全覆盖 而b那边表示有多少个区间在b左边结束 即可能被覆盖
然后就出现一个问题 为什么不会出现最下面这样的情况呢 这样子就会多减啊
但是因为区间长度是递增的 所以在[ a , b ]之前是不会出现长度大于该区间的线段的 所以这个是正确的
代码
#include <bits/stdc++.h> using namespace std; const int N = 4 * 1e5 + 5; int T,n,ans[N],c1[N],cnt,m,c2[N],a[N]; struct ques { int l,r,tim,del; }q[N],ins[N]; void clear( ) { memset(ans,-1,sizeof(ans)); memset(c2,0,sizeof(c2)); memset(c1,0,sizeof(c1)); } void init( ) { int tmp = 0,num = 0; for(int i = 1;i <= n;i ++) { int pos,opt; scanf("%d%d",& opt,& pos); if(opt == 0) { tmp ++; q[i].l = pos; q[i].r = pos + tmp; q[i].tim = i; if(q[i].tim<0) break; q[i].del = 1; ins[tmp].l = pos; ins[tmp].r = pos + tmp; a[++ num] = q[i].l; a[++ num] = pos + tmp; } else { q[i].l = ins[pos].l; q[i].r = ins[pos].r; q[i].del = -1; q[i].tim = i; if(q[i].tim<0) break; } } sort(a + 1,a + num + 1); m = unique(a + 1,a + num + 1) - a - 1; } int lowbit(int x) { return x & (-x); } void add1(int pos,int del) { while(pos <= m) { c1[pos] += del; pos += lowbit(pos); } } void add2(int pos,int del) { while(pos <= m) { c2[pos] += del; pos += lowbit(pos); } } int query1(int pos) { int ans = 0; while(pos >= 1) { ans += c1[pos]; pos -= lowbit(pos); } return ans; } int query2(int pos) { int ans = 0; while(pos >= 1) { ans += c2[pos]; pos -= lowbit(pos); } return ans; } void solve( ) { for(int i = 1;i <= n;i ++) { int pos1 = lower_bound(a + 1,a + m + 1,q[i].l) - a - 1; int pos2 = lower_bound(a + 1,a + m + 1,q[i].r) - a; if(q[i].del == 1) { int ans1 = query1(pos1); int ans2 = query2(pos2); ans[q[i].tim] = ans2 - ans1; } add1(pos1 + 1,q[i].del); add2(pos2,q[i].del); } } int main( ) { freopen("segment.in","r",stdin); freopen("segment.out","w",stdout); scanf("%d",& T); while(T --) { cnt ++; clear( ); scanf("%d",& n); init( ); solve( ); printf("Case #%d: ",cnt); for(int i = 1;i <= n;i ++) { if(ans[i] != -1) { printf("%d ",ans[i]); } } } }

这道题其实是一道数学题
emmmm就是很考思维 因为题目上说k < max(m,n) 我们假设m n 较大的那个是行数
那么也就是说我们至少有一行是空着的
那么除了这一行 每一行都可以乱搞 然后这空的一行来擦屁股 总能使每一列都合法
然而乱搞的每一行不一定合法啊 所以思路是一样的
对于每一行都留一个空位剩下的空位乱搞 然后这个空位来擦屁股
最后还需要特判一下这一行有没有填满 填满了就空不出位置了 判断一下填满的这行合不合法就可以了
但是这时候就会出现一个问题 我们的空行是被动填的 会不会出现最后的这一行不合法呢
答案是否定的 有三种情况 两边长分别是 奇 奇 偶 偶 奇 偶

对于每一个矩形 我们空出一行
1.奇 偶
绝对不合法 因为要合法 每一行每一列-1个数均为奇数个
那么-1的个数 = 奇数行 * 奇数个每行 = 奇数 偶数列 * 奇数个每列 = 偶数 矛盾了 所以不可能合法
2.偶 偶
总共有-1 偶 * 奇 = 偶数个 那么除去最后一行 剩下奇数行 * 奇数个 = 奇数
所以最后一行就有偶数 - 奇数 = 奇数个 肯定合法
3.奇 奇 和上面是一样的证明
所以就这么搞搞就出来了
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e6 + 10; int n,m,k,num[N][2]; ll ans = 1,poww[N],mod; void init( ) { poww[0] = 1; for(int i = 1;i <= 1000000;i ++) poww[i] = poww[i - 1] * 2 % mod; } int main( ) { freopen("number.in","r",stdin); freopen("number.out","w",stdout); scanf("%d%d",& n,& m); scanf("%d",& k); int numm = 0; for(int i = 1;i <= k;i ++) { int x,y,c; numm ++; scanf("%d%d%d",& x,& y,& c); num[x][0] ++; num[y][1] ++; } scanf("%I64d",& mod); init( ); int tag = 0; if((m + n) % 2 == 1) { printf("0"); return 0; } if(n < m) { swap(n,m); tag = 1; } if(m == 1) { printf("%I64d",poww[n - numm - 1]); return 0; } bool t = false; for(int i = 1;i <= n;i ++) { if(num[i][tag] == 0 && (! t)) { t = true; continue; } ans = ans * poww[m - 1 - num[i][tag]] % mod; } printf("%I64d",ans); }
今天真的考得很撇!!!!!!!!太垃圾了