「NOIP」联赛模拟测试32

PS：

身为一名 (20) 届学弟，面对考试无题解，题解少，出现了“千人看动动，万人颓吴迪”的现象。

至于 (skyh) 写了题解，但没有人看，具体原因，咱也不知道，咱也不敢问。

为了造福学弟，一定要多写题解，一定不会咕！！！

题面下载

循环依赖

签到题，没什么可说的，除了读入字符串有点麻烦，建个图，判个环，就完了。

• 关于读入字符串，我是这么做的：由于 (scanf) 只能读入一个字符串，不会读多余的东西（如，空格， ），所以每读完一个字符串，可以再读一字符，根据这个字符是空格还是 来判断是否停止读入。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <map>

typedef unsigned long long ull;

using namespace std;

const int maxn = 1e5 + 50, INF = 0x3f3f3f3f;
const ull base = 233;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int T, n, nodecnt;

struct Edge {
	int to, next;
} e[maxn * 3];

int tot, head[maxn];

inline void Add (register int u, register int v) {
	e[++ tot].to = v;
	e[tot].next = head[u];
	head[u] = tot;
}

map <ull, int> mp;

inline ull HASH (register char * str) {
	register int len = strlen (str + 1);
	register ull hash = 0;
	for (register int i = 1; i <= len; i ++) hash = hash * base + str[i] - '0';
	return hash;
}

int dfn[maxn], low[maxn], st[maxn];
bool vis[maxn];
int tic, top, sum;

inline void Init () {
	memset (st, 0, sizeof st);
	memset (vis, 0, sizeof vis);
	memset (dfn, 0, sizeof dfn);
	memset (low, 0, sizeof low);
	memset (head, 0, sizeof head);
	mp.clear (), tic = 0, top = 0, sum = 0, tot = 0, nodecnt = 0;
}

inline void Tarjan (register int u) {
	dfn[u] = low[u] = ++ tic, st[++ top] = u, vis[u] = 1;
	for (register int i = head[u]; i; i = e[i].next) {
		register int v = e[i].to;
		if (! dfn[v]) {
			Tarjan (v);
			low[u] = min (low[u], low[v]);
		} else if (vis[v]) {
			low[u] = min (low[u], dfn[v]);
		}	
	}
	if (dfn[u] == low[u]) {
		sum ++;
		while (st[top + 1] != u) {
			register int v = st[top --];
			vis[v] = 0;
		}
	}
}

int main () {
	freopen ("dependency.in", "r", stdin);
	freopen ("dependency.out", "w", stdout);
	T = read();
	while (T --) {
		register bool kill = 0;
		n = read(), nodecnt = 0, Init ();
		for (register int i = 1; i <= n; i ++) {
			register char str[11];
			scanf ("%s", str + 1);
			register ull uhash = HASH (str);
			if (! mp[uhash]) mp[uhash] = ++ nodecnt;
			register int u = mp[uhash];
			while (scanf ("%s", str + 1)) {
				register ull tmp = HASH (str);
				if (! mp[tmp]) mp[tmp] = ++ nodecnt;
				register int v = mp[tmp];
				if (u == v) kill = 1;
				Add (u, v);
				register char flag;
				scanf ("%c", &flag);
				if (flag == '
') break;
			}
		}
		if (kill) {
			puts ("Yes");
			goto end;
		}
		for (register int i = 1; i <= nodecnt; i ++) if (! dfn[i]) Tarjan (i);
		if (sum == nodecnt) puts ("No");
		else puts ("Yes");
		end:;
	}
	return 0;
}

A

20 pts

应该很好拿吧，(define ;int ;long ;long)，都能过。

20 pts + rp pts

可以发现，给出的二次函数，没有常数项，都是过原点的，将式子简单的化一下：

[ax^2+bx=x(ax+b) ]

(x) 是给定的，可以分为两种情况：

• (x) 为正数，((ax+b)) 取最大值。

• (x) 为负数，((ax+b)) 取最小值。

---

这样问题就转化成了求 ((ax+b)) 的极值，排一下序，乱搞一下，就有 (60;pts) 了。

如果你像 (skyh) 一样，(rp = INF)，你就可以将本题 (A) 掉。

100 pts

考场上距离正解就差那么亿点点，就直接原路返回了。

现在问题不是转化成了求 ((ax+b)) 的极值了吗，可以用单调栈维护一下上凸包和下凸包，来求出多个一次函数的极值。

以 维护最小值，上凸包 为例

将若干个一次函数的斜率 (a) 从大到小排序，以此推入栈中，分为两种情况：

• 插入后与之前的形成一个凸包，(i) 与 (top) 的交点的横坐标大于 (i) 与 (top-1) 的交点的横坐标，不用 (pop)。

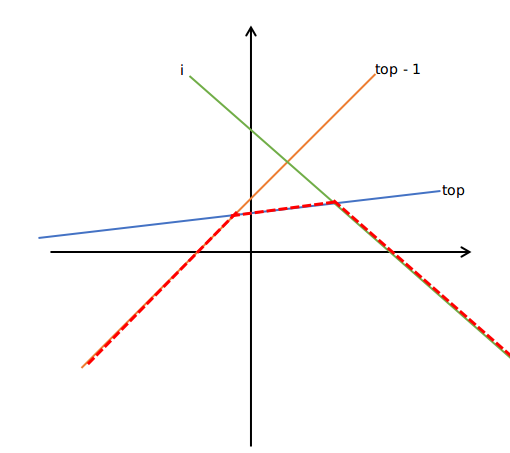
• 插入后与之前的形成一个新的凸包，(i) 与 (top) 的交点的横坐标小于 (i) 与 (top-1) 的交点的横坐标，需要 (pop)。

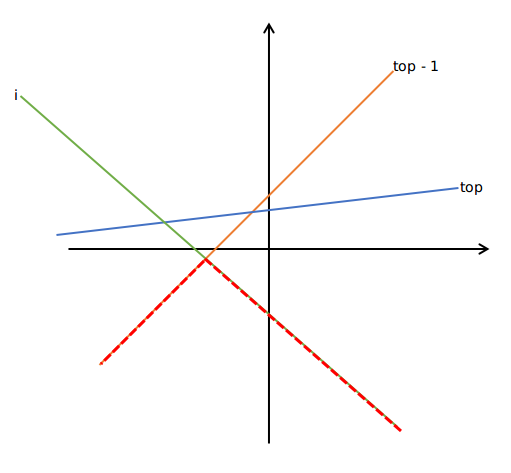
其他情况建议直接手摸，用 (sir) 的话来说：“就挺板子的”。

我们会发现，最后停留在栈中的每个函数片段就是我们所求的凸包，根据不同情况判断，跳一下即可。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

typedef long long ll;

using namespace std;

const int maxn = 5e5 + 50, INF = 0x3f3f3f3f;

inline ll read () {
	register ll x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, q, top, tmp;
int st[maxn];
ll ans1[maxn], ans2[maxn];

struct Node {
	ll a, b;
} a[maxn];

inline bool cmp1 (register Node x, register Node y) {
	return x.a > y.a;
}

inline bool cmp2 (register Node x, register Node y) {
	return x.a < y.a;
}

inline double Link (register int x, register int y) {
	return (double) (a[y].b - a[x].b) / (a[x].a - a[y].a);
}

inline ll Calc (register int i, register ll x) {
	return 1ll * a[i].a * x + 1ll * a[i].b;
}

int main () {
	freopen ("A.in", "r", stdin);
	freopen ("A.out", "w", stdout);
	n = read(), q = read();
	for (register int i = 1; i <= n; i ++) a[i].a = read(), a[i].b = read();
	top = 0, tmp = 1, sort (a + 1, a + n + 1, cmp1); // 最小值斜率从大到小
	for (register int i = 1; i <= n; i ++) { // 维护最小值，上凸包
		if (top && a[st[top]].a == a[i].a && a[st[top]].b <= a[i].b) continue;
		while (top && a[st[top]].a == a[i].a && a[st[top]].b > a[i].b) top --;
		while (top > 1 && Link (i, st[top - 1]) >= Link (i, st[top])) top --;
		st[++ top] = i;
	}
	for (register ll x = 32323; x >= 1; x --) {
		while (tmp < top && Calc (st[tmp], -x) >= Calc (st[tmp + 1], -x)) tmp ++;
		ans2[x] = Calc (st[tmp], -x);
	}
	top = 0, tmp = 1, sort (a + 1, a + n + 1, cmp2); // 最大值斜率从小到大
	for (register int i = 1; i <= n; i ++) { // 维护最大值，下凸包
		if (top && a[st[top]].a == a[i].a && a[st[top]].b >= a[i].b) continue;
		while (top && a[st[top]].a == a[i].a && a[st[top]].b < a[i].b) top --;
		while (top > 1 && Link (i, st[top - 1]) >= Link (i, st[top])) top --;
		st[++ top] = i;
	}
	for (register ll x = 1; x <= 32323; x ++) {
		while (tmp < top && Calc (st[tmp], x) <= Calc (st[tmp + 1], x)) tmp ++;
		ans1[x] = Calc (st[tmp], x);
	}
	while (q --) {
		register ll x = read();
		if (x >= 0) printf ("%lld
", 1ll * x * ans1[x]);
		else printf ("%lld
", 1ll * x * ans2[-x]);
	}
	return 0;
}

B

因为考场上撤硕，(skyh) 改题面没听到，考完我也没读懂题，向 ghosh 图草。

某人：哦，改题面了，忘了跟你说...

10 pts

显然 (5 imes 5 = 25) 的超强数据，直接暴搜显然会 (T)，发现好多状态被访问了多次，记忆化一下好了。

20 pts

会发现 (a_i=1) 时，有规律，(frac {num[1] + 1}{2})，很好找到吧～～

60 pts

当只有两个数的时候，可以分情况讨论：

• 在 (a[1]) 取完后，(a[2]) 没取完。

考虑 (a[2]) 在 (a[1]) 取完前取了 (i) 个，如果我们将每次取数的操作打成一个序列，当前情况如下：

最后一个取的必定是 (a[1])，答案是：

[frac{1}{2^{a[1] + i}} imes (a[1] + i) imes inom{a[1] + i - 1}{i} ]

意义：

一共选了 (a[1] + i) 个，步数就是 (a[1] + i)，由于选这段序列的时候 (a[1]) 和 (a[2]) 都未选完，所以要乘上每一位所需的概率 (frac{1}{2})。

再乘上前面那个线段里的 (a[1]) 和 (a[2]) 选择的顺序是任意的，所以乘上一个组合数。

---

• 在 (a[2]) 取完后，(a[1]) 没取完。

考虑 (a[2]) 取完后 (a[1]) 剩了 (i;(igeq 1)) （最后一个取的一定是 (a[1])，所以至少剩一个） 个，打成序列如下：

标红的是最后一个 (a[2])，显然后面取得只能全是 (a[1])，答案是：

[frac{1}{2^{a[1] + a[2] - i}} imes (a[2] + a[1]) imes inom{a[1] + a[2] - 1 - i}{a[2] - 1} ]

意义：

如果你理解了上面那个，这个不用我说，你应该就能理解。

显然这已经将 (a[1]) 和 (a[2]) 全选完了，所以步数就是 (a[1] + a[2]) 。

在取完最后一个 (a[2]) 之前，(a[1]) 和 (a[2]) 都还有，所以要乘上概率 (frac{1}{2})，但是取完最后一个 (a[2])，就只剩下 (i) 个 (a[1]) 了，概率就是 (1) 。

再乘上前面那个线段 (a[1]) 和 (a[2]) 任意选的组合数。

100 pts

如果你将 (60;pts) 轻易的打出来了，下面的可能需要你重新整理一下思路，正解与上面的说有关系，也没关系（啊巴啊巴啊巴）

首先引进一个函数 (f[i]) 表示 (a[i]) 被取的期望值，也就是选 (a[i]) 的期望次数。

由期望的线性性（(E_{a + b} = E_a + E_b)）得出：

[ans = a[1] + sum^{n}_{i=2}f[i] ]

很好理解吧～～

容易发现：

我们 (60;pts) 的做法，求的就是这个，但是，如果我们对每个 (a[i]) 都求一边，复杂度是 (Theta(n^2))，难以接受。

但是我们漏了一个很重要的条件 (a[i]leq 5 imes 10^5)，不妨求出每个值的期望次数，对于每个 (a[i])，在根据 (a[i]) 的值得到相应的概率。

由此，我们可以得到我们的 (f[a[i]]) 的式子：

[f[a[i]] = sum^{a[i] - 1}_{x=0} x imes frac{1}{2^{a[1] + x}} imes inom{a[1] + x - 1}{x} + a[i] imes (1-sum^{a[i] - 1}_{x=0} frac{1}{2^{a[1] + x}} imes inom{a[1] + x - 1}{x}) ]

会发现，式子跟之前那个出现了一点小差别，前半部分应该没问题，仍就是“在 (a[1]) 取完后，(a[2]) 没取完”的情况。

后面的式子我们用了一个 (1) 减去什么东东，很好理解，因为除了上面的情况，剩下的就是这样的情况了，所以直接用 (1) 减是正确的。

然后 (for) 循环直接求即可。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define int long long // 小朋友不要学坏

using namespace std;

const int maxn = 5e5 + 50, INF = 0x3f3f3f3f, mod = 323232323;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, ans, inv2, maxval;
int a[maxn], f[maxn], g[maxn];
int fac[maxn], facinv[maxn];

inline int qpow (register int a, register int b) {
	register int ans = 1;
	while (b) {
		if (b & 1) ans = ans * a % mod;
		a = a * a % mod;
		b >>= 1;
	}
	return ans;
}

inline void Init () {
	fac[0] = 1;
	for (register int i = 1; i <= 5e5; i ++) fac[i] = fac[i - 1] * i % mod;
	facinv[500000] = qpow (fac[500000], mod - 2);
	for (register int i = 5e5; i >= 1; i --) facinv[i - 1] = facinv[i] * i % mod;
}

inline int C (register int a, register int b) {
	if (a == b || a == 0 || b == 0) return 1;
	if (a < b) return 0;
	return fac[a] * facinv[b] % mod * facinv[a - b] % mod;
}

signed main () {
	freopen ("B.in", "r", stdin);
	freopen ("B.out", "w", stdout);
	n = read(), Init (), inv2 = facinv[2];
	for (register int i = 1; i <= n; i ++) {
		a[i] = read();
		if (i >= 2) maxval = max (a[i], maxval);
	}
	g[0] = C (a[1] - 1, 0) * qpow (inv2, a[1]) % mod;
	for (register int i = 1; i <= maxval; i ++) {
		g[i] = (g[i - 1] + C (a[1] + i - 1, i) * qpow (inv2, a[1] + i) % mod) % mod;
		f[i] = (f[i - 1] + i * C (a[1] + i - 1, i) % mod * qpow (inv2, a[1] + i) % mod) % mod;
	}
	for (register int i = 2; i <= n; i ++) {
		ans = (ans + (f[a[i]] + a[i] * (1 - g[a[i]] + mod) % mod) % mod) % mod;
	}
	printf ("%lld
", (ans + a[1]) % mod);
	return 0;
}

C

暂时只会一个一个跳...